Іі. Приклади розв`язку задач

1.39. Обчислити ранг матриці з допомогою елементарних перетворень

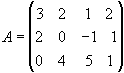
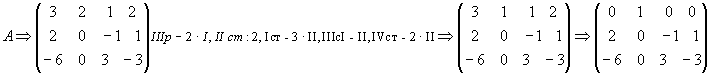де знак вказує, що з`єднані ним матриці одержуються одна із другої елементарними перетвореннями, а тому мають один і той же ранг.

Додамо далі до ІІІр+3 ІІ, Іст:2, додаючи його до ІІІст і віднімаючи із Ivст, і переставивши, нарешті, місцями перші два стовпця, будемо мати

 

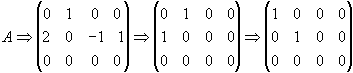
Ранг матриці А дорівнює 2, тобто r=2.

1.40. За допомогою елементарних перетворень обчислити ранг матриці

 

 

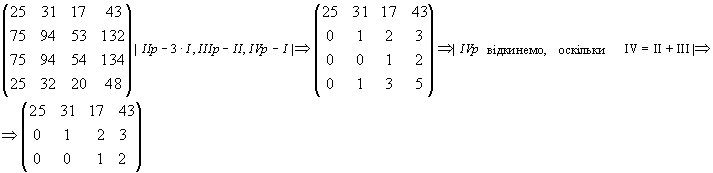
r=3, бо визначник трикутної матриці з перших трьох стовпців не дорівнює нулю. ^

 

Обчислення рангу матриці методом облямування

Вибираємо в даній матриці мінор другого порядку, відмінний від нуля. Потім обчислюємо мінори третього порядку, які облямовують (містять в собі) вибраний, поки не знайдемо серед них відмінного від нуля. Далі обчислюємо мінори четвертого порядку, які облямовують відмінний від нуля мінор ІІІ-го порядку, поки не знайдемо серед них відмінний від нуля, і т.д. Якщо знайшли відмінний від нуля мінор r-го порядку, а всі облямовуючі його мінори (r+1)-го порядку дорівнюють нулю або їх вже нема, то ранг матриці дорівнює r.

 

1.41. Обчислити ранг матриці

 Викреслили ІІІр., оскільки 2· ІІр.+І є ІІІр.

Виберемо, наприклад, 

 

Обчислимо мінори ІІІ-го порядку, які облямовують його

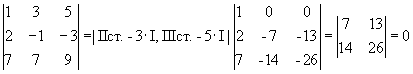
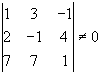 мінор ІІІ-го порядку відмінний від нуля.

 

Він міститься у визначнику IV порядку заданої матриці, який дорівнює нулю. Отже, r=3. ^

 

1.42. Розв`язати системи рівнянь

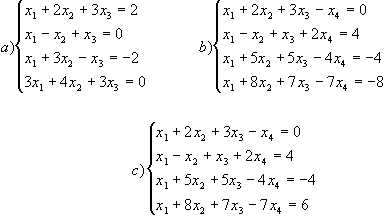
а) Тут r(A)=3, r(B)=3; система сумісна, визначена.

Оскільки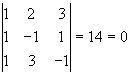 

 

тоді із перших трьох систем, наприклад, згідно формул Крамера знаходимо

х₁=-1, х₂=0, х₃=1

b) Тут r(A)=2, r(B)=2; система сумісна, але не визначена.

Визначник 

 

і із перших двох рівнянь системи

 

Знаходимо

,

де невідомим х₃ і х₄ можна надавати будь-які значення.

в) в цьому випадку r(A)=2, r(B)=3; і система несумісна.

1.43. Методом Гаусса (послідовного виключення невідомих) розв`язати однорідну систему рівнянь:

 

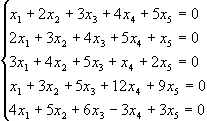
і знайти її фундаментальну систему розв`язків.

Випишемо розширену матрицю системи (при цьому нульовий стовпець можна, звичайно, не писати). Після зрозумілих перетворень будемо мати

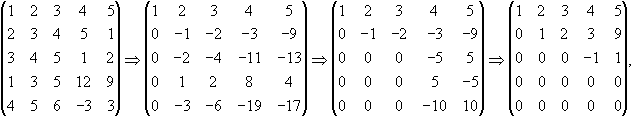тобто задана система рівнозначна наступній:

 

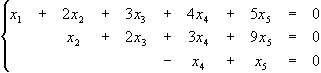
Тут r=3, і три невідомих можна виразити через останні, наприклад, так:

х₄=х₅

х₂=-2х₃-3х₄-9х₅=-2х₃-12х₅

х₁=-2х₂-3х₃-4х₄-5х₅=х₃+15х₅

Фундаментальну систему можна одержати, якщо вільним невідомим х₃, х₅ надавати значення х₃=1, х₅=0 (тоді х₁=1, х₂=-2, х₄=0) і значення х₃=0, х₅=1 (тоді х₁=15, х₂=-12, х₄=1). Це дає фундаментальну систему розв`язків:

e₁=(1, -2, 1, 0, 0), e₂=(15, -12, 0, 1, 1)

З використанням фундаментальної системи часто записують загальний розв`язок у вигляді лінійної комбінації розв’язків е₁ та е₂, тобто:

e=

 

1.44. Знайти фундаментальну систему розв`язків системи лінійних рівнянь та записати її загальний розв`язок

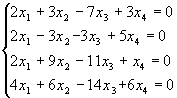
IVp. відкинемо (пропорційно до І), або IVp.=II+III, IIp.-I, IIIp.-I

 

Третій рядок відкинемо. Система звелась до драбинчастої з головними невідомими х₁, х₂ і вільними х₃, х₄:

 

З останнього рівняння . З першого Вільних невідомих 2. Тому беремо визначник ІІ порядку з одиничними елементами головної діагоналі і нульовими - побічної: .

Будемо вважати х₃=1, х₄=0. Тоді 

 

Одержимо вектор e₁=()

Далі будемо вважати х₃=0, х₄=1. Одержимо вектор e₂=

Вектори e₁ і e₂ являють собою фундаментальну систему розв`язків.

Тепер загальний розв`язок можна записати у вигляді

e=

Надаючи коефіцієнтам , будь-які (довільні) числові значення будемо одержувати різноманітні частинні розв`язки.

1.45.

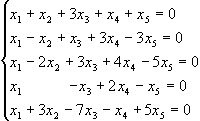
 /від усіх рядків віднімемо IV/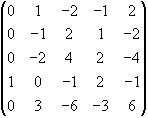 

 

II, III, V рядки, які пропорційні до І-го, викреслимо. В одержаній матриці переставимо І і ІІ стовпці:

 Ранг матриці дорівнює 2.

Головні невідомі х₂ і х₁. Вільні - х₃, х₄, х₅. Система тепер має вигляд:

 

Надаючи вільним невідомим послідовно значення, що дорівнюють елементам стовпців визначника

 

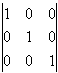
1) х₃=1, х₄=0, х₅=0; 2) х₃=0, х₄=1, х₅=0; 3) х₃=0, х₄=0, х₅=1

 

одержимо:

1) х₂=1, х₁=1; 2) х₂=1, х₁=-2; 3) х₂=-2, х₁=1

 

тобто вектори С₁=(1, 2, 1, 0, 0)

 

С₂=(-2, 1, 0, 1, 0)

 

С₃=(1, -2, 0, 0, 1)

 

складають фундаментальну систему розв`язків. Загальний розв`язок системи тепер залишиться.

c=

1.46.

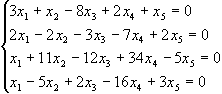
Матриця коефіцієнтів

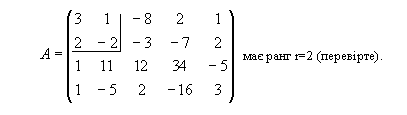
Виберемо за базисний мінор 

 

Тоді вкорочена система має вигляд:

 

Звідки, вважаючи х₃=с₁, х₄=с₂, х₅=с₃, знаходимо

 

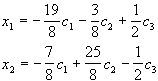
Загальний розв`язок системи

 

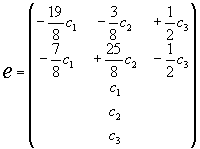
Із загального розв`язку знаходимо фундаментальну систему розв`язків

 

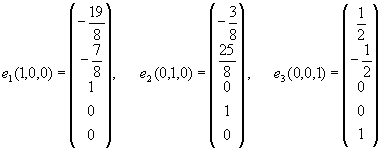
З використанням фундаментальної системи загальний розв`язок може бути записаний

e=с₁e₁+с₂e₂+с₃e₃