§ 6. Диференціал функції

Нехай функція диференційована в точці х, тобто існує границя

Згідно з теоремою 2 (гл. 5, §1) для всіх значень з досить малого околу точки х маємо рівність

де при . Звідси

де - нескінченно мала вищого порядку порівняно з .

 

Зауваження. Якщо, навпаки, в точці х для приросту функції має місце рівність

де - стала, то функція - диференційована в точці х і .

 

Дійсно, з останньої формули

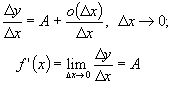
Визначення. Диференціалом функції точці х називається головна, лінійна відносно частина приросту функції в цій точці

Диференціалом незалежної змінної х вважатимемо його приріст , тобто . Отже, .

 

Зауваження. З останньої формули випливає, що . Саме тому похідну часто позначають або і розуміють її як відношення двох диференціалів: диференціала функції до диференціала аргументу.

Оскільки , то

,

і при досить малих має місце формула

якою часто користуються при наближених обчисленнях.

Для з’ясування геометричного змісту диференціала знову звернемося до рис.45. З трикутника :

.

 

Таким чином, диференціал функції дорівнює приросту ординати дотичної до графіка функції в точці .

 

З правил диференціювання випливають правила обчислень диференціалів функцій:

а) ;

 

б) ;

 

в) .

 

Для ілюстрації доведемо останнє правило.

Нехай , тоді

 

Встановимо формулу для диференціала складної функції , де і - диференційовані функції своїх аргументів, таким чином, вимоги теореми 2 (§3) виконані.

З одного боку, , де - незалежна змінна, а з іншого – в силу вищезгаданої теореми

 

де .

 

Отже, зовнішній вигляд диференціала функції зберігається і у випадку, коли є функцією, а не незалежною змінною.

Цю важливу властивість диференціала називають інваріантністю його форми. Її зручно використовувати для обчислення похідної функції, заданої параметрично.

Коротко зупинимося на такому способі завдання функції за допомогою двох функцій . Припустимо, що функція має обернену . Тоді, очевидно, у є деякою функцією від . Таким чином, пара функцій і визначають деяку функцію , задану параметрично. Допоміжна змінна при цьому називаєтьсяпараметром.

 

Припустимо, що функції і - диференційовані в кожній точці проміжку , причому при всіх . Враховуючи, що а , матимемо похідну від функції, заданої параметрично, у вигляді

 

§ 7. Диференціали вищих порядків

Нехай функція разів диференційована на проміжку Х. Тоді у кожній точці існує, зокрема, її диференціал , який надалі називатимемо також диференціалом першого порядку функції . Оскільки приріст аргументу величина стала, то є функцією однієї змінної х. Диференціал цієї функції називатимемо диференціалом другого порядку функції  і будемо позначати або . Отже, за визначенням, .

 

Далі маємо

 

І, нарешті, якщо для функції означено диференціал -го порядку , то диференціалом n-го порядку функції називається диференціал першого порядку від диференціала -го порядку, тобто

 

За індукцією ясно, що

 

З останньої формули випливає, що при довільному n

 

тобто похідну n-го порядку функції можна представити як відношення її диференціала n-го порядку до n-го ступеню диференціала аргументу.

 

Зауваження. Диференціали n-го порядку вже не мають властивості інваріантності форми. Дійсно, вже при , з одного боку, якщо - незалежна змінна, маємо . З іншого, для складної функції , де , маємо

 

де 

 

Оперуючи з диференціалами, зручно обчислювати похідні вищих порядків від функції, заданої параметрично за допомогою двох функцій .

 

Для конкретності зупинимося на випадку знаходження другої похідної , вважаючи функції і двічі диференційованими і .

 

Маємо послідовно і

 

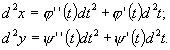
Але оскільки х – незалежна змінна, то , і тому

 

Отже, остаточно