Задача про неперервне нарахування процентів

На яку величину зросте капітал K₀, через n років при р% річних, якщо нарахування процентів здійснюють декурсивним методом – процентний платіж нараховується і додається до капіталу в кінці кожного розрахункового періоду. Декурсивне нарахування проценту найбільш поширене в світовій практиці.

Очевидно, що при р% річних розмір вкладу щорічно буде збільшуватися в раз, тобто в кінці n-го року маємо

 

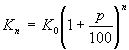
Отже капітал K₀ при річному нарахуванні складних процентів згідно ставки р% через n років зросте до величини K_n.

 

де:

 - процентна ставка, виражена в десяткових дробах.

 - складний декурсивний коефіцієнт.

Якщо нараховують проценти не один раз на рік, а m раз, при тому ж щорічному прирості р%, процент нарахування за частину року складе , а розмір вкладу за n років при mn нарахуваннях складе

 (1)

Припустимо, що проценти нараховуються кожні півроку , кожний квартал , щомісячно , кожний день , кожний час і т.д. неперервно .

 

Якщо число розрахункових періодів прямує до нескінченності, то можна стверджувати, що період розрахунку прямує до нуля.

Знайдемо границю величини К_mn при (n – число років, m – число розрахункових періодів в році).

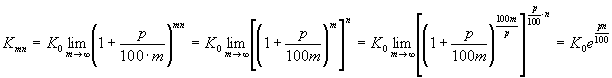 (2)

 

Отже, ми вивели формулу для кінцевої величини капіталу при неперервному нарахуванні складних процентів. Вона є неперервною функцією і дозволяє обчислити величину капіталу в будь-якій період часу.

Наведемо таблицю розмірів вкладів К_mn (якщо К₀=1грошова одиниця, р=5%, n=20 років) згідно формули складних процентів (1) і формули неперервного нарахування процентів

 

	формула складних процентів (1)					формула неперервного нарахування процентів (2)
	m=1	m=2	m=4	m=12	m=365
розмір вкладу, гр. од.	2,6335	2,6851	2,7015	2,7126	2,7181	2,7182

 

Різниця між щорічним нарахуванням (m=1) і неперервним нарахуванням формула (2) незначна (близько 2,5%).

Зауваження. В практичних фінансово-кредитних операціях неперервне перерахування процентів застосовується рідко. Воно є досить ефективним при аналізі складних фінансових проблем, наприклад, при обгрунтуванні і виборі інвестиційних рішень.

 

§6 Нескінченно малі та нескінченно великі функції

Визначення 1. Функція f(x) називається нескінченно малою при х>х₀ (або в точці х₀), якщо f(x)=0.

Нескінченно малу в точці функцію коротко часто називають просто нескінченно малою.

Визначення 2. Функція f(x) називається нескінченно великою при х>х₀ (або в точці х₀), якщо f(x)= .

Нескінченно велику в точці функцію коротко називають просто нескінченно великою.

Властивості нескінченно малих та нескінченно великих виконані для будь-яких послідовностей (див. §1), справедливі і для функцій загального випадку, при доведенні яких повторюється процедура аналогічна тій, якою скористалися при встановленні теореми §2. Пропонуємо зробити це самостійно.

Зазначимо нарешті, що визначення 1, 2 мають місце, звичайно ж, і для випадків х>х₀±0, х>±, х>.

При дослідженні функцій часто доводиться мати справу не з однією, а з кількома нескінченно малими функціями в даній точці. Для їх порівняння вивчають частку цих функцій. Детально зупинимося на правилах порівняння нескінченно малих.

 

Визначення 3. Нехай функція а(х) і b(х) нескінченно малі в точці х₀.

 

Тоді

1. якщо 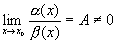(А R), то  (х) і  (х) називаються нескінченно малими одного порядку при х>х₀;

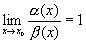2. якщо , то  (х) і  (х) називаються еквівалентними нескінченно малими при х>х₀; записується:  (х)  (х), х>х₀.

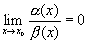3. якщо , то  (х) називається нескінченно малою вищого порядку порівняно з  (х) при х>х₀. Цей факт записується так:  =0( ).

Словом 0( ) є загальним позначенням для нескінченно малої вищого порядку, ніж  .

Наприклад, можна писати:

1-cos x=0(x), tg x-sin x=0(x) і т.д.