5.2. Розв'язок і дослідження систем рівнянь першого порядку методом повного виключення (Метод Гаусса).

Формули Крамера дають можливість, використовуючи прийом обчислення визначників, знайти числові значення розв'язку системи рівнянь у випадку, коли визначник основної матриці системи відмінний від нуля. Але практичне застосування цих формул в багатьох випадках ускладнено. Перш за все необхідно відмітити, що для знаходження розв'язків за формулами (3) необхідно обчислити n+1 визначник n-го порядку, що представляє собою досить трудомістку роботу, навіть при використанні тих прийомів, які були вказані в §4. Але найголовніше те, що у випадку, коли коефіцієнти рівняння задані наближено (в реальних задачах це буває майже завжди), похибка розв'язку може бути досить велика. Це пояснюється тим, що доданки, які входять у кожний із визначників, через які визначається розв'язок системи, можуть бути досить великі (нагадаємо, вони представляють собою добуток n співмножників - різних коефіцієнтів розширеної матриці системи), а сам визначник, що представляє собою алгебраїчну суму таких доданків, може бути малий. Навіть в тому випадку, коли коефіцієнти в системі вихідних рівнянь відомі точно, але самі обчислення ведуться з урахуванням лише заданого числа значущих цифр, ми з тих же причин зможемо одержати досить великі похибки в результаті. А тому при практичному розв'язку систем рівнянь в більшості випадків використовують не формули Крамера, а інші прийоми обчислень.

В даному курсі ми розглянемо метод повного виключення, стосовно розв'язку систем рівнянь 1-ого порядку також і в тому випадку, коли число рівнянь не співпадає з числом невідомих. Але викладення цього методу почнемо з основного випадку: коли число рівнянь співпадає з числом невідомих.

Таким чином, нехай знову задана система n рівнянь з n невідомими:

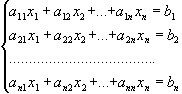 (1)

 

Оскільки хоча б один із коефіцієнтів a_i1 відмінний від нуля (інакше в систему взагалі не входило б х₁), і рівняння в системі можливо мінять місцями, тоді без будь-якого обмеження загальності можна вважати, що Поділимо 1-ше рівняння системи на a₁₁ і приведемо його до виду 

 

де

 

Перемножуючи всі члени одержаного рівняння на а_і1 і віднімаючи із і-го рівняння системи (1), одержимо нову систему

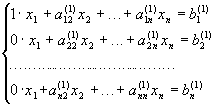 (2)

де

i=1, 2, ..., n; k=1, 2, ..., n

 

Оскільки рівняння системи (2) одержані як лінійні комбінації рівнянь системи (1), то будь-який розв'язок системи (1) є також і розв'язком системи (2). Разом з тим оскільки

 

то рівняння системи (1) можуть бути одержані як лінійна комбінація рівнянь системи (2). Отже будь-який розв'язок системи (2) є і розв'язком системи (1). Таким чином, система (1) і (2) рівнозначні. (Лінійною комбінацією двох рівнянь с₁₁х₁+с₁₂х₂+...+с_1nх_n=d₁ і, с₂₁х₁+с₂₂х₂+...+с_2nх_n=d₂ будемо називати рівняння

 ₁(c₁₁x₁+c₁₂x₂+...+c_1nx_n)+ ₂(c₂₁x₁+c₂₂x₂+...+c_2nx_n)= ₁d₁+ ₂d₂, де  ₁ та  ₂ - числа)

Порівняємо тепер визначники D₁ і D₂ основних матриць систем (1) і (2). Перший рядок основної матриці системи (2) одержаний із першого рядка основної матриці системи (1) діленням на а₁₁. Така операція відповідає діленню D₁ на а₁₁. Інші рядки одержані відніманням із відповідних рядків основної матриці системи (1) величин, пропорційних першому рядку. Ця операція не змінює величини визначника. Звідси виходить, що визначник D₂ основної матриці системи (2) дорівнює . А тому D_2 0, якщо D_1 0 і D₂=0, якщо D₁=0. Відмітимо, нарешті, що обчислення ми проводили тільки з коефіцієнтами рівнянь системи (1), тому немає необхідності писати самі рівняння. Достатньо написати лише розширену матрицю системи і перетворити тільки елементи цієї матриці.

Будемо позначати перехід від однієї розширеної матриці до другої, тобто фактично перехід від однієї системи рівнянь до системи, їй рівнозначної, символом  або ~. Тоді проведені операції можна записати так:

 

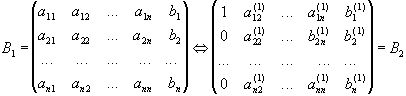
Будемо вважати спочатку, що визначник D₁ основної матриці системи (1) відмінний від нуля. Тоді, як сказано вище, , а тому в крайньому випадку одне з чисел (і=1, 2, ..., n) відмінне від нуля, оскільки, якби всі дорівнювали нулю, дорівнював би нулю і визначник D₂ основної матриці системи (2).

Оскільки рівняння в системі (2) можна міняти місцями, тому, без обмеження, можна вважати, що . Поділимо 2-е рівняння системи (2) на , помножимо одержаний рядок на (і=1, 3, 4, ..., n) і віднімемо від і-го рядка.

Тоді будемо мати

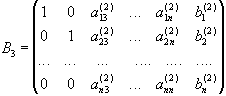
Система рівнянь, що відповідає матриці В₃, рівнозначна системі (2), а тому і вихідній системі (1). Визначник D₃ основної матриці цієї системи відмінний від нуля, оскільки відмінний від нуля визначник D₂. Звідси, в крайньому випадку одне із чисел (і=3, ..., n) відмінне від нуля і можна знову провести ті ж операції, що і раніше. Продовжуючи аналогічні міркування, після n операцій одержимо матрицю

 

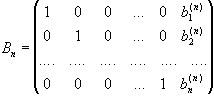
Відповідна система рівнянь має вигляд

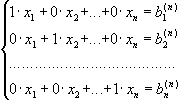 (3),

 

її єдиним розв'язком є (4)

 

Оскільки система (3) рівнозначна системі (1), має єдиний розв’язок, то має єдиний розв'язок, що визначається формулами (4), і вихідна система(1).

 

Приклад 1. Розв’язати систему

 

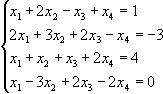
Розв’язок

x₁=1; x₂=-1; x₃=0; x₄=2

 

Відмітимо, якщо система однорідна, тобто всі числа b_i (і=1, 2, ..., n) дорівнюють нулю, тоді дорівнюють нулю і всі числа Тому система (1) має в цьому випадку тільки нульовий розв’язок.

Нехай тепер визначник D₁ основної матриці системи (1) дорівнює нулю. Тоді вже не можна стверджувати, що серед чисел (і=m, m+1, ..., n), одержаних після (m-1)-го етапу перетворень, буде хоча б одне, відмінне від нуля. Більше того, на якомусь етапі всі ці числа обов’язково стануть рівними нулю (інакше ми мали б розібраний випадок). Таким чином, нехай одержана матриця

 

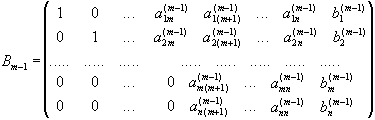
Переставимо m-ий стовпець матриці на місце n-го, а всі наступні за m-м стовпцем, крім стовпця вільних членів зсунемо на одне місце вліво (така операція, очевидно, означає перестановку невідомих в рівняннях системи або їх перенумерацію, що, звичайно, не змінює розв’язку системи). В результаті одержимо матрицю

 

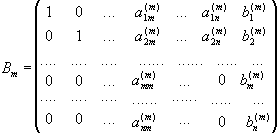
де

 і=1, 2, ..., n;

 k=m, m+1, ..., n.

 

Продовжуючи ті ж перетворення, що раніше, одержимо в кінцевому рахунку матрицю

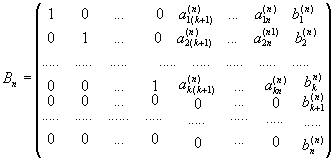 (5)

Матриці (5) відповідає система рівнянь

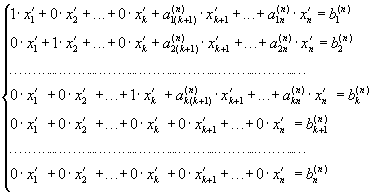 (6)

в якій невідомі відрізняються від невідомих х_і в системі (1) лише нумерацією. Оскільки система (6) рівнозначна системі (1), тоді висновок про розв’язність системи (1) рівносильний висновку про розв’язність системи (6).

Очевидно, що якщо хоча б одне із чисел (і=k+1, ..., n) не дорівнює нулю, тоді рівняння системи (6), а тому і рівняння системи (1), несумісні. Якщо є всі (і=k+1, ..., n) дорівнюють нулю, тоді рівняння сумісні. При цьому невідомим можна надати будь-які значення, і система має такі розв’язки:

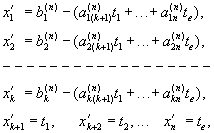
де t₁, t₂, ..., t_e (=n-k) довільні

Для того, щоб було зручно повертатися до вихідної системи невідомих, корисно над стовпцями матриць, які одержуються при проведенні перетворень, надписувати позначення відповідних невідомих. Вкажемо, крім того, що якщо вихідна система (1) однорідна, тоді всі числа (і=1, 2, ..., n) дорівнюють нулю. Тому мають місце такі два твердження.