§ 3 Лінійна залежність та лінійна незалежність системи векторів

Нехай задано k векторів: . Назвемо таку задану множину векторів системою векторів.

 

Визначення. Система векторів називається лінійно-залежною, якщо хоча б один із векторів системи може бути виражений як лінійна комбінація останніх.

Таким чином система векторів лінійно-залежна, якщо, наприклад,

 (1)

де а₁,а₂,….. а_k-1 - деякі числа.

Відмітимо, якщо в задану систему (множину) векторів включений нульовий вектор, тоді система обов‘язково лінійно-залежна. Дійсно, завжди можна написати що , тобто виражати нульовий вектор як лінійну комбінацію (з нульовими коефіцієнтами) останніх векторів системи.

Наведене визначення лінійної залежності системи векторів виділяє із інших один якийсь вектор системи. Щоб уникнути такого виділення, часто вводять друге визначення лінійної залежності.

 

Визначення. Система векторів називається лінійно-залежною, якщо існують числа , із яких хоча б одне відмінне від нуля, такі що

 (2)

 

Таке визначення, звичайно, рівнозначне попередньому. Дійсно, якщо маємо рівність

,

тоді, переносячи в праву частину, отримаємо =0, і, отже, маємо рівність (2) при . Навпаки, якщо виконана умова (2) і, наприклад, , тоді

,

 

і тим самим виконана умова (1).

В повній відповідності зі сказаним можна ввести і визначення лінійної незалежності систем векторів, як заперечення лінійної залежності.

 

Визначення. Система векторів називається лінійно-незалежною, якщо вона не є лінійно-залежною.

Наведемо інші, рівнозначні визначення:

система векторів називається лінійно-незалежною, якщо ні один із векторів системи не може бути виражений як лінійна комбінація останніх;

система векторів називається лінійно-незалежною, якщо рівність нулю їх лінійної комбінації можлива тільки тоді, коли всі коефіцієнти лінійної комбінації дорівнюють нулю.

Найпростішим прикладом лінійно-залежних векторів є пара колінеарних векторів. Нехай задані два колінеарних ненульових вектора і . Позначимо через відношення довжин цих векторів, тобто число . Очевидно, що вектори і при зробленому виборі числа мають однакові довжини. Отже, якщо і однаково направлені, тоді , якщо ж вони направлені в протилежні сторони, тоді . Таким чином, два колінеарних вектора завжди лінійно залежні. Ясно, що вірне і обернене твердження: якщо два вектори лінійно залежні, тоді вони колінеарні.

Таким чином, умова

 (3),

 

тобто умова лінійної залежності двох ненульових векторів, є умова, необхідна і достатня для колінеарності цих векторів.

Доведемо тепер, що лінійна залежність трьох векторів є умова необхідна і достатня для їх компланарності.

Нехай задані три компланарні ненульові вектори . У відповідності з визначенням при співставленні початків цих векторів вони опиняться в одній площині (рис. 8).

 

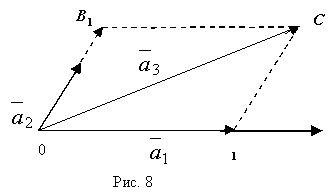
Будемо вважати, що вектори і не колінеарні (в противному випадку вони лінійно залежні). Через кінець вектора (точку С) проведемо прямі, паралельні векторам і . Ці прямі перетнуть прямі, на яких лежать вектори і , в точках А₁ і В₁. Вектори ОА₁ і , очевидно, колінеарні. А тому , і аналогічно . Але . Таким чином, , і, отже, вектори лінійно залежні.

Справедливе і обернене твердження: якщо вектори лінійно залежні, то вони компланарні. Дійсно, нехай . Якщо вектори і не колінеарні, то вони визначають деяку площину. В тій же площині лежать, очевидно, вектори і , а тому і їх сума – вектор . Якщо ж вектори і колінеарні, тоді на тій же прямій лежить і вектор , і три заданих вектора не тільки компланарні, але і колінеарні.

Із наведених міркувань випливає, що якщо на площині задана пара неколінеарних векторів, то будь-який третій вектор, який лежить в тій же площині, може бути представлений як лінійна комбінація двох заданих.

 

Визначення. Впорядкована пара (якщо вказано, який вектор пари вважається першим, а який другим) неколінеарних векторів називається базисною системою векторів (базисом) на площині, визначеної заданими векторами.

Теорема розкладу. Будь-який вектор на площині може бути представлений як лінійна комбінація базисної системи векторів, це представлення (розклад по базисній системі) єдине.

Нехай вектори і базисні. Тоді, як показано вище, будь-який вектор може бути представлений у вигляді . Залишається довести єдинність розкладу.

Будемо вважати, що існує ще один розклад вектора по тій же базисній системі:

при цьому хоча б одне із чисел та відмінне від чисел та . Тоді отримаємо . Отже вектори і лінійно залежні, а тому колінеарні. Але це суперечить твердженню, що і утворюють базисну систему. Таким чином, розклад заданого вектора по заданій базисній системі єдиний.

Проведені міркування легко переносяться і на вектори, задані в просторі.

 

Визначення. Впорядкована трійка (якщо вказано, який вектор трійки вважати першим, який другим і який третім) некомпланарних векторів називається базисною системою векторів (базисом) в просторі.

Теорема розкладу. Будь-який вектор може бути представлений як лінійна комбінація базисної системи векторів; таке представлення (“розклад по базисній системі”) єдине.

Доведення. Нехай задана базисна система векторів і - довільний вектор. Нехай 0 – загальний початок цих векторів. Через точку D – кінець вектора (рис. 9) – проведемо пряму DE, паралельну вектору, і нехай E - точка перетину цієї прямої з площиною, визначену векторами і .

 

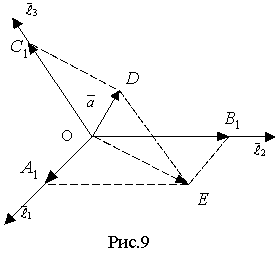
Через точку Е проведемо прямі, паралельні векторам і , нехай В₁ і А₁ – точки перетину цих прямих з прямими, на яких лежать вказані вектори. Нарешті, через точку D проведемо пряму, паралельну ОЕ до перетину в точці С₁ з прямою, на якій лежить вектор .

 

Маємо

 

Тому

Одержаний розклад єдиний, оскільки, якби існував ще один розклад

,

то виконувалась би рівність

,

 

при цьому хоча б одне із чисел було б відмінне від нуля. Це означало б що вектори були б лінійно залежні, а тому і компланарні, що суперечить умові теореми.

Із доведеного випливає також, що будь-які чотири вектори лінійно залежні.

Введемо ще одне суттєво важливе поняття.

 

Визначення. Координатами вектора в заданому базисі називаються коефіцієнти розкладу вектора по базисній системі векторів.

Отже, якщо задана базисна система векторів і то координатами вектора в заданому базисі називаються числа . Записуються координати вектора в заданому базисі у вигляді рядка: .

 

Зустрічається також запис у вигляді стовпця

 

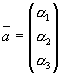
Таким чином, якщо заданий базис , і в цьому базисі , тоді .

 

Очевидно, якщо заданий деякий базис, то задання координат вектора в цьому базисі повністю визначає сам вектор, і , отже, два вектора рівні тоді і тільки тоді, коли рівні їх координати в якому-небудь заданому базисі.

Використовуючи правила лінійних операцій, отримаємо такі теореми:

 

При множенні вектора на число всі його координати в заданому базисі перемножуються на це число.

При додаванні векторів складаються відповідні координати цих векторів.

Дійсно, нехай заданий базис , і в цьому базисі два вектори:

, .

 

Тоді

;

 

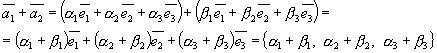
Відмітимо, що в просторі можливо вибрати нескінченну множину базисних систем векторів, і один і той вектор в різних базисних системах буде мати різні координати. В багатьох задачах корисно переходити від однієї базисної системи до другої і встановлювати співвідношення між координатами вектора в різних системах. Покажемо це на прикладах.