§ 7 Основні операції з матрицями

В попередньому параграфі широко застосовувались лінійні операції з рядками і стовпцями різних матриць. Але в деяких питаннях лінійної алгебри доводиться розглядати операції з матрицями як з єдиним об`єктом.

В основі вивчення операцій з матрицями лежить поняття рівності матриць. Будемо виходити з такого визначення: дві матриці однієї і тієї ж розмірності називаються рівними, якщо рівні всі їх відповідні елементи.

Отже, матриці А і В однієї і тієї ж розмірності nxm рівні тоді і тільки тоді, коли A_ik=B_ik i=1, 2,..., n; k=1, 2,..., m. При цьому ще раз підкреслимо, що порівнювати можна лише матриці однієї і тієї ж розмірності.

Сумою двох матриць А і В однієї і тієї ж розмірності nxm називається матриця С тієї ж розмірності така, що

(С)_ik=(A)_ik+(B)_ik (1)

Отже, при додаванні матриць (додавати можна тільки матриці однієї і тієї ж розмірності) треба складати всі їх відповідні елементи.

Оскільки додавання матриць зводиться до додавання чисел - елементів цих матриць, очевидно, має місце комутативна і асоціативна властивість.

А+В=В+А; (А+В)+С=А+(В+С) (2)

Добутком матриці А на число  (або числа  на матрицю А) називається матриця В така, що

(В)_ik= (A)_ik (3),

тобто при множенні матриці на число (або числа на матрицю) необхідно всі елементи матриці помножити на це число. Нагадаємо, що при множенні на число визначника матриці достатньо було помножити на це число лише елементи будь-якого рядка (або стовпця).

Легко перевірити, що при множенні матриці на число має місце розподільча властивість:

 (А+В)= А+ В; ( + )= А+ В (4)

Визначимо тепер добуток двох матриць. Нехай дана матриця А розмірності nxm і матриця В розмірності mxp.

 

Визначення. Добутком матриці А розмірності nxm на матрицю В розмірності mxp називається матриця С розмірності nxp така, що

 (5),

інакше кажучи, для одержання елементу, що знаходиться в і-ому рядку і в k-ому стовпцю матриці добутку, потрібно обчислити суму добутків елементів і-го рядка першого множника і відповідних елементів k-го стовпця другого множника. Отже, для того щоб можливо було скласти вказану суму, потрібна рівність числа стовпців в першій матриці (тобто число елементів в кожному рядку) числу рядків у другій (тобто числу елементів в кожному стовпці).

 

Приклад 1.

 

Знайти А В

Розв`язок. Матриця А має розмірність 3х2, матриця В 2х2; добуток існує - це матриця розмірності 3х2.

 

Добуток матриць не має переставної властивості: А В, взагалі кажучи, не дорівнює В А.

По-перше, із того, що можна обчислити А В, зовсім не виходить, що має зміст В А. Наприклад, в тільки що розібраному прикладі перестановка множників, тобто множення В на А неможливе оскільки не можна матрицю розмірності 2х2 помножити на матрицю розмірністю 3х2 - число стовпців першої матриці тут не дорівнює числу рядків другої. Але навіть якщо добуток В А існує, то нерідко . Розглянемо приклад.

Нехай . Тоді

 

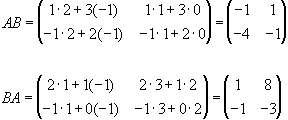
Разом з тим можливо довести (таке доведення ми рекомендуємо провести читачу), що

(А В) С=А(В С) (6)

 

А (В+С)=АВ+АС

(звичайно приймається до уваги, що всі ці добутки мають зміст).

У відповідності із визначенням добутку матриць завжди можливо множення квадратних матриць одного порядку, при цьому добуток буде матрицею того ж порядку. Відмітимо без доведення одну із властивостей добутку квадратних матриць одного порядку: визначник добутку двох матриць одного і того ж порядку дорівнює добутку визначників матриць, що перемножуються.

Дуже часто доводиться розглядати добуток матриці розмірності nxm на матрицю розмірності mx1, тобто на матрицю з одним стовпцем. Очевидно, ми повинні одержати в результаті матрицю розмірності nx1, тобто також матрицю з одним стовпцем. Нехай, наприклад, необхідно помножити матрицю

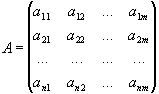 на матрицю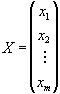 

 

В результаті одержимо матрицю 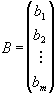, елементи якої обчислюються за формулами:

 

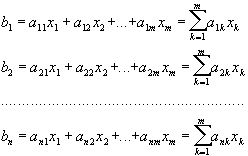
Але це означає, що систему рівнянь 1-ого порядку, розглянуту в попередньому параграфі, можна записати в дуже зручній матричній формі: АХ=В.

Суттєву роль в різних застосуваннях матричної алгебри відіграє квадратна матриця, у якої всі діагональні елементи (тобто елементи, які знаходяться на головній діагоналі) дорівнюють 1, а всі інші елементи дорівнюють нулю. Така матриця називається одиничною матрицею. Очевидно, що визначник одиничної матриці

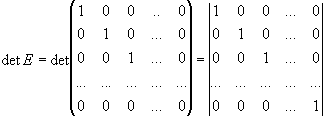 = 1

 

Характерні наступні властивості одиничної матриці: нехай задана квадратна матриця А порядку n і Е-одинична матриця того ж порядку. Тоді АЕ=ЕА=А.

Дійсно але 

 

Тому в сумі відмінні від нуля тільки ті складові, для яких e=k. Отже, (АЕ)_ік=(А)_ік , і звідси АЕ=А. Аналогічно одержуємо і для добутку ЕА.