5.1. Дослідження форми еліпсоїда
Знайдемо, насамперед, переріз еліпсоїда площиною х=0.
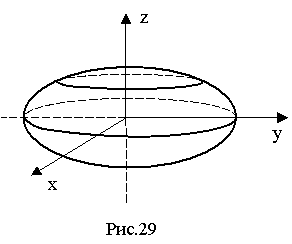
В перерізі (рис.29) одержимо лінію, визначену системою:
х=0, 
Таким чином, в площині yz маємо еліпс з напівосями b і с. Розглянемо тепер переріз поверхні площинами, паралельними площині ху, тобто площинами z=h. В перерізі одержимо лінії, визначені системою
z=h, 
Очевидно,
якщо |h| c,
тоді в перерізі одержимо уявне місце
точок, при |h|=c одержимо
точки (0;0;с), якщо h 0
і (0;0;-с), якщо h 0.
Ящо ж 
с,
в площині z=h одержимо
еліпс
z=h,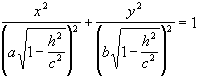 
,
тобто еліпс з напівосями
і 
При h=0 напівосі еліпса дорівнюють а і b, зі збільшенням h напівосі зменшуються до нуля (при h=с). Вигляд поверхні показаний на рис. 29.
Очевидно, що поверхня, яка розглядається, симетрична відносно координатних площин, осей і початку координат. Вся поверхня не виходить із прямокутного паралелепіпеда зі сторонами 2а, 2b, 2с, симетричного відносно координатних площин.
Якщо дві осі еліпсоїда рівні між собою, тоді еліпсоїд можна одержати обертанням еліпса навколо одної із осей, і сама поверхня називається тоді еліпсоїдом обертання.
Наприклад, якщо b=c, тоді поверхня має рівняння
і може бути одержана обертанням еліпса
z=0, 
навколо осі х.
Якщо а=b=с, тоді рівняння еліпсоїда набуває вигляду
x2+y2+z2=a2 ,
і поверхня представляє собою сферу з центром на початку координат і радіусом а.
Таким чином, сфера є частинний випадок еліпсоїда, коли всі його напівосі дорівнюють між собою.
5.2. Дослідження форми однопорожнинного гіперболоїда
Знайдемо переріз однопорожнинного гіперболоїда
площиною рисунка, тобто площиною х=0 (рис.30).
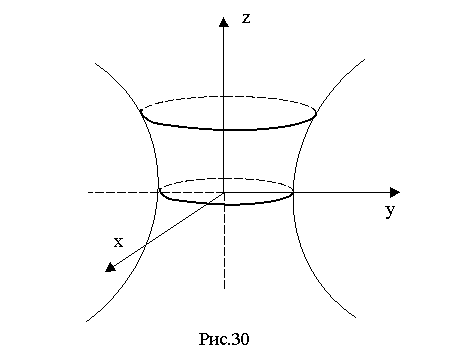
Лінія перетину визначається системою рівнянь
х=0, 
В перерізі маємо гіперболу з напівосями b і с, причому дійсна вісь гіперболи співпадає з віссю у.
Розглянемо переріз поверхні площиною z=h, паралельній площині ху. В перерізі одержуємо лінію, визначену системою рівнянь
z=h, 
або системою
z=h, 
Таким чином, у вибраних паралельних перерізах маємо еліпси, напівосі яких зростають зі збільшенням |h|. Найменший еліпс (він називається горловим еліпсом) одержуємо при h=0. Очевидно, однопорожнинний гіперболоїд симетричний відносно координатних площин, осей і початку координат.
Якщо a=b, тоді поверхня може бути утворена обертанням гіперболи
х=0, 
навколо осі z.
5.3. Дослідження формули двопорожнинного гіперболоїда
В перетині двопорожнинного гіперболоїда
площиною рисунка (тобто площиною х=0) одержуємо гіперболу (рис. 31).
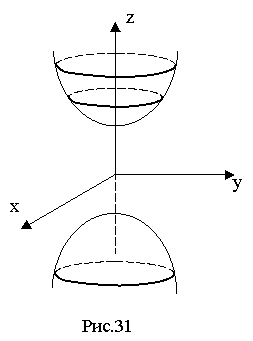
х=0, 
Перетинаючи поверхню площинами z=h, одержимо при |h| c уявне місце точок, при h= с точки (0;0;с) і (0;0;-с), при |h| с еліпси
z=h, 
Поверхня, очевидно, симетрична відносно площин, осей і початку координат.
5.4. Дослідження формули еліптичного параболоїда
В перерізі еліптичного параболоїда
площиною рисунка (тобто площиною х=0) одержуємо параболу x=0, y2=2b2z (рис. 32)
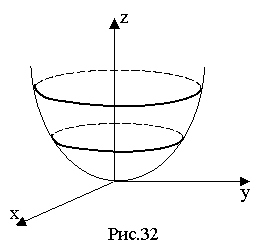
Перетинаючи поверхню площинами z=h (h 0), одержуємо еліпси
z=h, 
Вся поверхня лежить “над” площиною ху, симетрична відносно площин хz і yz і відносно осі z.
Якщо a=b , маємо параболоїд обертання
x2+y2=2a2z ,
який можна одержати обертанням параболи
x=0, y2=2а2z
навколо осі z.
Відмітимо, що всі параболи, що одержуються в перерізі параболоїда обертання площинами, які проходять через вісь z, мають загальний фокус.