§4. Диференційованість елементарних функцій

У попередньому параграфі розглянуто правила обчислення похідних для функцій однієї змінної. Вони дозволяють знаходити похідні будь-яких елементарних функцій.

Доведемо, що всі основні елементарні функції (за винятком ) диференційовані на своїх областях визначення, причому виконуються формули, які запишемо в окрему так звану таблицю похідних:

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

11. .

12. 

.

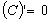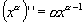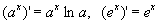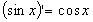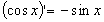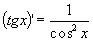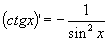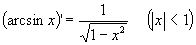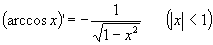Доведення 1. Нехай на деякому проміжку Х задано сталу функцію . Тоді для довільних точок і маємо і . Отже, , а тому і і .

 

Для скорочення доведення подальших формул подаємо їх у конспективному вигляді.

2.

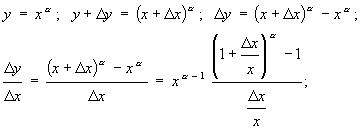
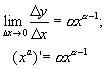
(враховано формулу (3) гл.5, §7).

 

3.

 

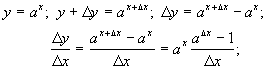
(враховано формулу (2) гл. 5, §7). Зокрема, при отримаємо .

 

4.

 

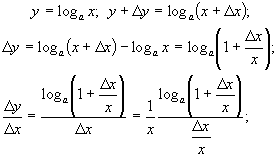
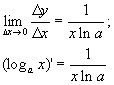
(враховано формулу (1) гл. 5, §7). Зокрема, при отримаємо.

 

5.

 

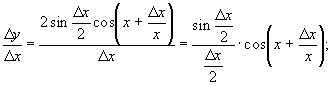
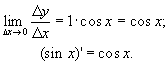
(враховано першу важливу границю (гл.5 §5) і неперервність функції ).

 

6. Для знаходження похідної функції представимо її у вигляді і розглянемо як складну функцію: , . Тоді і . Отже, , так що .

 

7. За правилом диференціювання частки маємо

 

8. Аналогічно доводиться, що .

 

9. Функція є оберненою до функції , причому похідна при не дорівнює нулю. А тому за правилом диференціювання оберненої функції

 

(Перед коренем обрано знак плюс, оскільки при ).

 

Отже,

 

10. Аналогічно доводиться, що

 

11. Функція є оберненою до функції , причому похідна при не дорівнює нулю. А тому за правилом диференціювання оберненої функції

Отже, .

 

12. Аналогічно доводиться, що

.

 

На закінчення наведемо формулу диференціювання показниково-ступеневої функції , де і - диференційовані функції.

За правилом диференціювання складної функції маємо

,

так що .

 

Підкреслимо ще раз, що таблиця похідних разом з правилами диференціювання складають основу диференціального числення. Користуючись ними, можна знайти похідні від функцій, які утворені за допомогою арифметичних операцій та суперпозицій над основними елементарними функціями, тобто перейти від будь-яких елементарних функцій, знову до елементарних. Отже, операція диференціювання не виводить з класу елементарних функцій.

§5. Похідні вищих порядків

Нехай функція має похідну на проміжку Х. Якщо в точці похідна , в свою чергу, диференційована, то її похідну називають похідною другого порядку або другою похідною функції в точці і позначають одним із символів .

Визначення 1. Нехай функція має на проміжку Х похідні . Якщо в точці існує похідна функції , то її називають похідною n-го порядку функції в точці і позначають одним із символів , .

 

Отже, якщо функція має в точці х похідні до n-го порядку включно, то .

 

Визначення 2. Функція , яка має на деякому проміжку Х похідні до n-го порядку включно, називається n разів диференційованою на Х. Функція, яка має на Х похідні всіх порядків, називається нескінченно диференційованою на Х.

 

З визначення 1 безпосередньо випливає, що

,

 

де і - довільні сталі, а і - n разів диференційовані функції.

У загальному випадку для обчислення похідної вищого порядку потрібно попередньо знайти похідні всіх нижчих порядків. В окремих випадках вдається встановити загальний вираз для похідноїn-го порядку.

Знайти похідну n-го порядку функції . Маємо послідовно

 

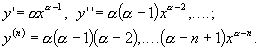
Зокрема, при маємо , а при відповідно 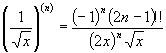, де символом позначено добуток натуральних чисел, які не перевищують n і мають з nоднакову парність (наприклад, ).

 

Для виразу має місце формула: . Зокрема, при маємо

 

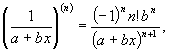
а при відповідно

 

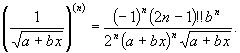
Знайти похідну n-го порядку функції . Враховуючи, що , матимемо

 

Знайти похідну n-го порядку функції . Маємо послідовно

 

Зокрема, якщо , то .

 

Знайти похідну n-го порядку функції . Маємо послідовно

 

У загальному випадку, як неважко бачити,

 

Цілком аналогічно