§4 Застосування функцій в економіці

Спектр використання функцій в економіці досить широкий. Найбільш часто використовуються в економіці такі функції:

1. Функція корисності - залежність корисності, тобто результату, ефекту деякої дії від рівня (інтенсивності) цієї дії.

2. Виробнича функція - залежність результату виробничої діяльності від обумовлюючих його факторів.

3. Функція випуску (частковий вид виробничої функції) – залежність обсягу виробництва від обсягу продукції.

4. Функція витрат (частковий вид виробничої функції) – залежність витрат виробництва від обсягу продукції.

5. Функція попиту, споживання і пропозиції - залежність обсягу попиту, споживання або пропозицій на окремі товари або послуги від різних факторів (наприклад ціни, доходу і т.д.)

Враховуючи, що економічні явища і процеси обумовлені діями різних факторів, для їх дослідження широкого використовуються функції багатьох змінних.

Якщо дією побічних факторів можливо знехтувати, або вдається зафіксувати ці фактори на певних рівнях, то залежність одного головного фактора вивчається з допомогою функції однієї змінної.

 

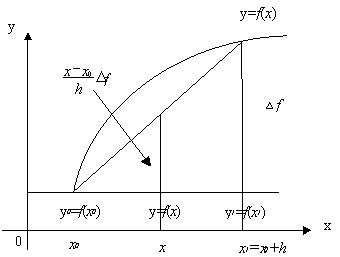
Рис. 42

 

Зупинимося на одному важливому прикладі застосування функції в економіці – використання таблиць функцій, які дозволяють зробити можливими різні розрахунки, виключити або спростити громіздкі обчислення.

При обчисленні за допомогою таблиць доводиться стикатися з ситуацією, коли аргумент функції заданий з більшою точністю, ніж дозволяє таблиця. В такому випадку бажано вдатися доінтерполяції – наближеного знаходження невідомих значень функцій по відомим її значеннях в заданих точках.

Найбільш простим є лінійне інтерполювання, при якому допускається, що приріст функції пропорційний приросту аргументу. Якщо задане значення х лежить між наведеними в таблиці значеннями і , яким відповідають значення функції і , то вважають, що (рис. ).

 

Величини називаються інтерполяційними поправками. Ці величини обчислюються за допомогою таблиці або наводяться в додатку до таблиці.

Якщо згідно заданим значенням функції необхідно знайти наближене значення аргументу, то необхідно здійснити обернене інтерполювання.

 

Приклад 4. Функція задана таблицею:

 

X	2	2,04	2,08
Y	2,42	2,88	3,38

1. Використовуючи лінійне інтерполювання, знайти .

2. Чому дорівнює х, якщо 

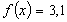
1.Маємо ; 

Згідно інтерполяційної формули одержимо .

 

2. Обернене інтерполювання можна здійснити по тій же формулі, але потрібно поміняти місцями змінні х і у:

,

 

де - невідоме значення оберненої функції.

Маємо у₀=2,88; 

.

 

Згідно інтерполяційної формули одержимо

Точність знаходження невідомих значень за допомогою лінійного інтерполювання незавжди є достатньою, а тому використовують ще й інші методи інтерполювання, наприклад, квадратичне інтерполювання.

Розв’язок задач

Приклад 5. Знайти область визначення функцій.

 

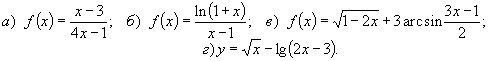
а) Функція визначена, якщо , тобто якщо .

 

б) Функція визначена, якщо , тобто якщо Отже, об’єднуючи два інтеграли, маємо .

 

в) Перший додаток дійсний при , а другий – при . Отже необхідно розв’язати систему нерівностей

 

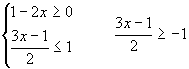
В результаті одержимо: .

 

Отже, областю визначення функції є відрізок 

 

г) Область визначення функції знайдемо із системи нерівностей

 звідси , або .

 

Приклад 6. Знайти множину значень функції.

Виділимо повний квадрат, одержимо . Перший доданок є невід’ємним, а тому функція приймає значення не менше –4. Отже множина значень функції є проміжок[-4; + ).

 

б) Оскільки , або . Помножимо нерівність на 5 і додамо до всіх частин цієї подвійної нерівності 4, маємо . Отже множиною значень функції є проміжок .

 

Приклад 7. З’ясувати парність (непарність) функцій:

 

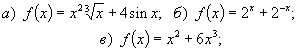
а) Замінюючи х на –х, одержимо

.

 

Тобто . Отже функція непарна.

б) Маємо ; тобто . Отже - парна.

в) Маємо . Таким чином і , тобто функція не є ні парною ні не парною.

 

Приклад 8. Знайти основні періоди функцій:

а) Оскільки основний період функції є , то для функції він дорівнює тобто ;

 

б) Тут перший доданок має період , а другий - . Очевидно, що основний період даної функції є найменше загальне кратне чисел , тобто .