
- •Конспект лекцій з курсу
- •§2 Визначники матриць другого порядку
- •§3. Визначники матриць третього порядку
- •§ 4 Визначники матриць вищих порядків
- •Приклади розв’язання задач
- •§5 Розв'язок систем n рівнянь із n невідомими
- •5.1. Правило Крамера
- •5.2. Розв'язок і дослідження систем рівнянь першого порядку методом повного виключення (Метод Гаусса).
- •1. Система однорідних рівнянь 1-ого порядку завжди сумісна.
- •2. Якщо визначник системи однорідних рівнянь 1-ого порядку дорівнює нулю, тоді система має нескінченну множину розв 'язків.
- •§ 6 Ранг матриці, теорема про сумісність систем рівнянь першого порядку
- •Іі. Приклади розв`язку задач
- •Обчислення рангу матриці методом облямування
- •§ 7 Основні операції з матрицями
- •Приклади розв`язку задач
- •§ 8 Обернена матриця, розв`язок матричних рівнянь
- •Іі. Приклади розв`язку задач
- •§9. Модель багатогалузевої економіки
- •Глава іі: Векторна алгебра
- •§1 Основні поняття
- •§2 Лінійні операції з векторами.
- •§ 3 Лінійна залежність та лінійна незалежність системи векторів
- •Приклади розв‘язку задач
- •§4 Проекція вектора на ось
- •§5 Прямокутна декартова система координат в просторі
- •§6 Скалярний добуток векторів
- •§7 Векторний добуток векторів
- •§8 Мішаний добуток векторів
- •Іі. Приклади розв’язку задач
- •Глава ііі: Аналітична геометрія
- •§1 Відповідність між геометричними образами та рівняннями
- •§ 2 Лінійні образи - площина і пряма
- •§ 3 Лінії другого порядку
- •Приклади розв`язку задач
- •§4 Перетворення координат на площині. Застосування перетворення координат до спрощення рівнянь кривих другого порядку.
- •§5 Циліндричні поверхні з твірними, паралельними координатним осям; поверхні другого порядку
- •5.1. Дослідження форми еліпсоїда
- •5.2. Дослідження форми однопорожнинного гіперболоїда
- •5.3. Дослідження формули двопорожнинного гіперболоїда
- •5.4. Дослідження формули еліптичного параболоїда
- •5.5. Дослідження форми гіперболічного параболоїда
- •6. Дослідження форми конуса 2-го порядку
- •Приклади розв`язку задач
- •§6 Полярна система координат на площині. Циліндрична і сферична системи координат в просторі
- •6.1. Полярна система координат на площині
- •6.2. Циліндрична система координат
- •6.3. Сферична система координат
- •Приклади розв’язку задач
- •Розділ іі. Вступ до математичного аналізу
- •Глава IV: Функції
- •§1 Поняття множини
- •§2. Абсолютна величина дійсного числа
- •§3. Поняття функції
- •§4 Застосування функцій в економіці
- •Розв’язок задач
- •Глава V: Границя і неперервність
- •§1 Поняття границі послідовності
- •1.1 Збіжні послідовності
- •1.2 Нескінченно малі і нескінченно великі.
- •§2 Основні властивості збіжних послідовностей
- •§3 Поняття границі функції
- •3.1 Визначення границі функції
- •3.2 Односторонні границі
- •3.3 Границя функції на нескінченності і нескінченні границі
- •§4 Властивості границь
- •§5 Перша і друга важливі границі
- •5.1 Перша важлива границя
- •5.2 Друга важлива границя
- •Задача про неперервне нарахування процентів
- •§6 Нескінченно малі та нескінченно великі функції
- •§7 Неперервність функції
- •Розв’язки задач
- •Розділ ііі. Диференціальне числення
- •Главаvi: Похідні та диференціали
- •§ 1 Поняття похідної
- •§2 Зміст похідної
- •2.1. Задача про дотичну до кривої
- •2.2. Задача про миттєву швидкість
- •2.3. Задачі про витрати виробництва та виручку
- •§3. Правила диференціювання
- •3.1 Диференціювання суми, добутку й частки
- •3.2. Диференціювання складної функції
- •§4. Диференційованість елементарних функцій
- •§5. Похідні вищих порядків
- •§ 6. Диференціал функції
- •§ 7. Диференціали вищих порядків
- •§8 Розв'язки задач
- •§ 9 Економічний зміст похідної.
- •Глава 7: Застосування похідних до дослідження функцій
- •§ 1 Загальні властивості функцій, неперервних на замкненому проміжку
- •§ 2 Теореми про середнє значення
- •§ 3 Правила Лопіталя
- •§4 Дослідження функцій
- •4.1. Умови монотонності функцій
- •4.3. Знаходження найменшого й найбільшого значень
- •4.4 Опуклість, угнутість та точки перегину кривої
- •3.5. Асимптоти. Дослідження графіка функції в цілому
- •§ 5 Застосування похідної в економічній теорії.
- •§ 5. Розв’язки задач
§ 5. Розв’язки задач
Приклад 9. Визначити проміжки монотонності функції
![]() .
.
Область
визначення ![]() .
.
Знаходимо
похідну ![]() і
розв’язуємо нерівності
і
розв’язуємо нерівності ![]() та
та ![]() .
При
.
При ![]() похідна
похідна ![]() ,
а при
,
а при ![]() похідна
похідна ![]() .
.
Отже,
в інтервалі (-4,4) функція зростає, а в
інтервалі ![]() функція
спадає.
функція
спадає.
Приклад 10. Дослідити на екстремум функцію
![]() .
.
а)
Область визначення ![]() .
Знаходимо
.
Знаходимо ![]() і
визначаємо критичні точки
і
визначаємо критичні точки
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Отже, ![]() .
.
Застосовуючи перше правило дослідження на екстремум, будуємо таблицю
|
Х |
|
-1 |
(-1,1) |
1 |
|
|
|
- |
0 |
+ |
+ |
- |
|
Y |
|
min
|
|
max
|
|
б)
Область визначення ![]() .
Знаходимо похідну
.
Знаходимо похідну ![]() .
.
Прирівнюємо її до нуля і знаходимо стаціонарну точку:
![]() .
.
Застосовуючи друге правило, знайдемо другу похідну і отримаємо
![]() .
.
Обчислимо
значення другої похідної в стаціонарній
точці. При ![]() маємо
маємо
![]() ,
,
отже
згідно достатньої умови другого типу
в точці ![]() функція
має мінімум
функція
має мінімум
![]() .
.
Приклад
11. Знайти найбільше і найменше значення
функції ![]() на
відрізку [-2,3].
на
відрізку [-2,3].
![]() .
Знаходимо похідну
.
Знаходимо похідну
![]() ;
;
![]() ,
,
тобто ![]() -
стаціонарні точки.
-
стаціонарні точки.
Визначаємо
значення функції в цих точках ![]() .
.
Обчислюємо
значення даної функції на границях
проміжку: ![]() .
.
Із отриманих чотирьох значень вибираємо найбільше і найменше. Отже, найбільше значення функції на заданому відрізку дорівнює 2, а найменше дорівнює -18.
Приклад 12. Знайти точку перегину і інтервали випуклості функції
![]() .
.
Знаходимо
похідну ![]() та
другу похідну
та
другу похідну ![]() і
будуємо таблицю, враховуючи, що
і
будуємо таблицю, враховуючи, що ![]() при
при ![]() .
.
|
х |
|
0 |
|
|
|
+ |
0 |
- |
|
y |
|
~ |
|
Отже,
на проміжку ![]() графік
функції - угнутий, а на проміжку
графік
функції - угнутий, а на проміжку ![]() -
опуклий. Точка
-
опуклий. Точка ![]() ,
в якій друга похідна змінює знак з “+”
на “-“ - точка перегину графіка.
,
в якій друга похідна змінює знак з “+”
на “-“ - точка перегину графіка.
Приклад
13. Знайти асимптоти кривих а) ![]() ;
б)
;
б) ![]() .
.
а)
Досліджувана функція має вертикальну
асимптоту ![]() .
Очевидно,
.
Очевидно,
![]() ,
,
функція має розрив другого роду.
Знаходимо
похилу асимптоту ![]() :
:
![]() ;
;

Отже, ![]() являється
похилою асимптотою кривої
являється
похилою асимптотою кривої
![]() .
.
б)
Очевидно, вертикальних асимптот
крива ![]() не
має. Якщо
не
має. Якщо ![]() .
Отже вісь Ох є
горизонтальною асимптотою даної кривої.
Дослідимо наявність похилої асимптоти:
.
Отже вісь Ох є
горизонтальною асимптотою даної кривої.
Дослідимо наявність похилої асимптоти:
![]() .
.
Отже,
є тільки горизонтальна асимптота ![]() .
.
Приклад 14. Дослідити функцію
![]()
І побудувати її графік.
1.
Область визначення ![]() .
Функція парна, оскільки
.
Функція парна, оскільки ![]() і
графік її симетричний відносно осі
ординат.
і
графік її симетричний відносно осі
ординат.
2. Вертикальних асимптот немає, оскільки функція визначена при всіх дійсних значеннях х.
Поведінка функції на нескінченності:
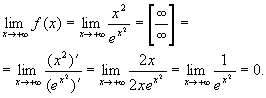
В
силу парності функції ![]() ,
тобто пряма
,
тобто пряма ![]() (вісь
абсцис) – горизонтальна асимптота.
(вісь
абсцис) – горизонтальна асимптота.
3. Екстремуми і інтервали монотонності:
![]() ;
;
![]() при
при ![]() ;
;
![]()
тобто
критичні точки ![]() .
.
Таким
чином ![]() є
точка максимуму,
є
точка максимуму, ![]() -
точка мінімуму,
-
точка мінімуму, ![]() -
точка максимуму.
-
точка максимуму.
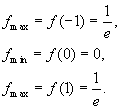
Функція
зростає на інтервалах ![]() і
і ![]() і
спадає на (-1;0) і
і
спадає на (-1;0) і ![]() .
.
4. Інтервали опуклості та вгнутості і точки перегину:
![]() .
.
![]() при
при ![]() .
.
Таким чином, функція опукла на інтервалах
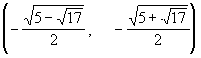 і
і 
і вгнута на інтервалах
 і
і 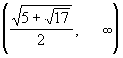
а ![]() -
точки перетину.
-
точки перетину.
5. ![]() . Рівняння
. Рівняння ![]() має
єдиний розв’язок х=0, тобто графік
функції проходить через початок
координат.
має
єдиний розв’язок х=0, тобто графік
функції проходить через початок
координат.
Приклад 15. Дослідити функцію
![]()
і побудувати її графік.
1.
Область визначення ![]() . Дана
функція не являється ні парною, ні
непарною.
. Дана
функція не являється ні парною, ні
непарною.
2. Досліджувана функція має вертикальну асимптоту х=3.. Очевидно,
![]()
отже в точці х=3 функція має розрив другого роду. Далі
![]() .
.
Знаходимо
похилу асимптоту ![]() .
.
![]()
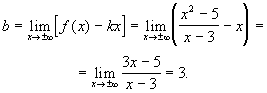
Отже, y=x+3 являється
похилою асимптотою кривої ![]() .
.
3.
Обчислимо похідну функції ![]() і
розв’яжемо рівняння
і
розв’яжемо рівняння
![]() :
:
х=5, х=1.
Досліджуючи знак похідної, складаємо таблицю
|
Х |
|
1 |
(1,3) |
(3,5) |
5 |
|
|
|
+ |
0 |
- |
- |
0 |
+ |
|
Y |
|
max
|
|
|
min
|
|
4. Знаходимо другу похідну
![]() .
.
Бачимо,
що рівняння ![]() коренів
не має, отже точок перегину не існує.
Будуємо таблицю:
коренів
не має, отже точок перегину не існує.
Будуємо таблицю:
|
Х |
|
|
|
|
- |
+ |
|
Y |
|
|
5.
Рівняння ![]() ,
тобто
,
тобто ![]() має
два корені
має
два корені ![]() ,
тобто графік перетинає вісь абсцис в
точках
,
тобто графік перетинає вісь абсцис в
точках ![]() .
.
На підставі добутих даних будуємо графік функції
(с) Київський інститут інвестиційного менеджменту, 2000 рік
Часопис "Наша справа" №13е, 2000 р.
