4.3. Знаходження найменшого й найбільшого значень

Зупинимося на питанні про відшукання найменшого й найбільшого значень функції , неперервної на відрізку [a;b]. За теоремою Вейєрштрасса (див. гл.7, §1) така функція обов’язково набуде цих значень в деяких точках [a;b]. Це можуть бути як внутрішні точки відрізка, так і його кінці.

Отже, для відшукання найменшого (найбільшого) значення неперервної на [a;b] функції потрібно знайти її локальні екстремуми на (a;b) і порівняти їх із значеннями . Найменше (найбільше) із цих значень і буде найменшим (найбільшим) значенням функції на відрізку [a;b].

Може статися, що функція на (a;b) зовсім не має точок екстремуму. В цьому випадку її найменше (найбільше) значення буде серед значень і .

 

При практичній роботі слід мати на увазі, що оскільки найменше (найбільше) значення досягається в критичних точках або на кінцях відрізку, то не потрібно перевіряти достатні умови наявності екстремуму функції в критичних точках. Досить лише знайти значення функції в усіх критичних точках і порівняти їх із значеннями , . Найменше (найбільше) з них і буде найменшим (найбільшим) значенням функції на [a;b].

 

Приклад 4. З пункту А, який лежить на лінії прямолінійної залізниці, в пункт В, що знаходиться від цієї лінії на відстані , потрібно перевозити вантажі. Вартості перевозу одиниці вантажу на одиницю відстані залізницею і дорогою дорівнюють відповідно m і n . До якої точки М лінії залізниці слід прокласти дорогу, щоб транспортування вантажу з А до В було найбільш економічним?

 

Нехай ,

 

тоді (рис.54а). Вартість перевезення k одиниць вантажу по дорозі ВМ складе , залізницею МА - відповідно. Загальна вартість транспонування вантажу

 

Рис.54

.

 

Знайдемо найменше значення цієї функції при .

 

Беручи похідну

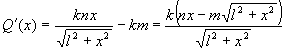
і прирівнюючи її до нуля, отримаємо рівняння , розв’язок якого визначає єдину критичну точку . Легко перевірити, що похідна в цій точці змінює знак з мінуса на плюс. Отже, якщо , тобто CM<CA, то при вартість транспортування вантажу з А в В найменша.

Якщо ж при , тобто (рис.54б), то дорогу слід, очевидно, прокласти вздовж прямої ВА.

 

4.4 Опуклість, угнутість та точки перегину кривої

Відносно функції , графік якої подано на рис.55 , припускається, що вона має неперервну другу похідну.

Визначення 1. Крива зветься опуклою (угнутою) в деякий точці М, якщо в околі цієї точки лежить під (над) дотичною, проведеною в точці М (на рис.55 в точці крива опукла, - угнута).

Крива зветься опуклою (угнутою) на деякому проміжку, якщо вона опукла (угнута) в усіх точках цього проміжку.

 

 

Рис. 55

При побудові графіка дуже важливо знати, на яких проміжках графік функції опуклий і на яких він угнутий.

Теорема 5. Якщо на проміжку (a;b) друга похідна функції від’ємна, то крива опукла на цьому проміжку; якщо ж додатна на (a;b), то крива угнута.

Представимо лише деякі міркування геометричного характеру. Якщо скрізь на проміжку (a;b), , то це означає, що сама функція, тобто - спадна. Отже, спадає на розглянутому проміжку кутовий коефіцієнт дотичної () до кривої і, звичайно, спадає й кут , утворюваний дотичною з віссю ОХ (рис. 56)

Очевидно, крива в усіх точках проміжку (a;b), розташована під дотичною, тобто вона опукла.

Якщо , то такі ж геометричні міркування доводять, що крива буде угнутою (рис. 77).

Визначення. Точка, яка відокремлює опуклу частину неперервної кривої від угнутої чи навпаки, зветься точкою перегину кривої.

На рис. точка є точкою перегину. У точках перегину дотична перетинає криву, бо з одного боку від цієї точки крива лежить під дотичною, а з другого боку - над нею.

 

Теорема. Якщо друга похідна функції в деякій точці стає , а при переході через цю точку змінює знак, то точка кривої з абсцисою є точкою перегину.

 

Доведення. Припустимо, що в точці М з абсцисою і змінює знак, наприклад, з плюса на мінус. Тоді ліворуч від М крива угнута , а праворуч – крива опукла . Отже, в точці М крива змінює угнутість на опуклість, а точка М є точкою перегину.

 

Приклад 5. Знайти точки перегину та визначити проміжки опуклості та угнутості кривої .

Маємо .

Друга похідна стає нулем при . Якщо , то; коли .

Таким чином, на проміжку графік опуклий, а на проміжку - угнутий. Точка кривої з абсцисою є точкою перегину.

Приклад 6. Дослідити на точки перегину криву .

Маємо . При . Досліджуємо зміну знака. При (крива угнута), при (крива теж угнута). Друга похідна не змінює знака, крива не має точок перегину.