§ 3 Правила Лопіталя

При дослідженні функцій часто виникає необхідність знаходити границі дробу , чисельник і знаменник якого при прямують до нуля або до нескінченності. Знаходження таких границь називають розкриттям невизначеностей. Найбільш простими і ефективними методами розкриття невизначеностей є правила Лопіталя.

Теорема 1. (перше правило Лопіталя). Нехай функції і диференційовані на інтервалі (a;b); і на (a;b). Тоді, якщо існує (скінчена або нескінченна) границя

,

 

то границя також існує і .

 

Доведення. Нехай і . Довизначимо функції і у точці а, припустивши . Тоді вони, очевидно, стануть неперервними на відрізку і задовольнятимуть на ньому всі вимоги теореми Коші попереднього параграфа. А тому знайдеться така точка , що

.

 

Якщо , то й . Переходячи до границі в останній рівності, маємо

,

 

що й потрібно довести.

 

Зауваження 1. Теорема 1 доведена для правих границь. Вона лишається вірною й для лівих, і до границі взагалі.

 

Зауваження 2. Твердження теореми 1 залишається в силі, якщо . Дійсно, візьмемо, наприклад, . Припустимо, і нехай , тоді

.

 

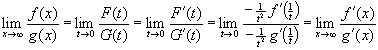При розкритті невизначеностей іншого типу діє теорема, яка наводиться без доведення.

 

Теорема 2. (друге правило Лопіталя). Нехай функції і диференційовані на інтервалі (a;b); і на (a;b). Тоді, якщо існує (нескінченна або скінченна) границя , то границя також існує і .

 

Зауваження, подані до теореми 1, залишаються в силі і для теореми 2.

Трапляється, що для похідних і виконуються умови однієї з теорем, тоді правила Лопіталя можна застосовувати повторно:

.

 

Взагалі, при виконанні відповідних умов цю процедуру можна застосовувати кілька разів.

Теорема 1 і 2 застосовуються до випадків, коли обидві функції і при прямують одночасно до нуля або до нескінченності.

Відповідно, знаходження називають розкриттям невизначеностей типу або .

 

За допомогою тотожних перетворень до основних випадків або можна звести й невизначеності інших типів: .

 

Невизначеність , тобто добуток , де , зводиться до вигляду або за формулами

 або .

 

Невизначеність зводиться до вигляду за допомогою перетворення

.

 

Невизначеності мають місце при розгляді функцій , якщо функція прямує відповідно до 0,1 і , а - відповідно до 0,1 і 0, коли . Як правило, використовується рівність

 

і справа зводиться до розкриття невизначеності вигляду у показнику

 

Приклад 1. Знайти наступні границі:

а) ;

 

б) ;

 

в) .

 

а) Чисельник і знаменник прямують до нуля, якщо , а тому маємо невизначеність типу . Використаємо правило Лопіталя, тобто розглянемо границю відношення похідних заданих функцій:

,

 

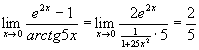оскільки і , якщо .

 

б) Невизначеність типу . Застосовуючи двічі формулу Лопіталя, одержимо:

.

 

На кожному етапі застосування правила Лопіталя слід користуватися тотожними перетвореннями, які спрощують відношення, а також комбінують це правило з будь-якими іншими прийомами обчислення границь.

в) .

 

Звільнимо знаменник дробу від множника , оскільки він має границю 1 при . Розкладемо чисельник, як різницю кубів

 

і звільнимо чисельник від множника , який має границю 3 при . Після таких спрощень отримаємо

.

 

Використовуючи першу важливу границю, отримаємо кінцеву відповідь , вже без правила Лопіталя.

 

Приклад 2. Знайти границі

а) ;

 

б) ;

 

в) ;

 

г) ;

 

д) .

а) Тут ми маємо невизначеність типу . Представимо добуток у вигляді частки, а потім, отримавши невизначеність типу  , застосуємо правило Лопіталя:

.

 

б) Це невизначеність типу . Для того, щоб знайти границю функції, приведемо дроби до загального знаменника, а потім, отримавши невизначеність типу , застосуємо правило Лопіталя:

.

 

в) Це невизначеність типу . Позначимо дану функцію через y , тобто , і прологарифмуємо її:

.

 

Обчислимо границю логарифма даної функції, застосовуючи правило Лопіталя (тут маємо невизначеність типу ):

.

 

Отже, .

 

г) Це невизначеність типу . Припустимо, , і прологарифмуємо:

;

 

Застосувавши правило Лопіталя, отримаємо:

.

 

Звільнимо знаменник від множника , оскільки він прямує до 1, якщо ;

.

 

Тобто .

 

д) Це невизначеність типу . Введемо позначення

.

 

Тоді є невизначеністю типу . Перетворимо вираз до вигляду

.

 

Згідно правила Лопіталя, отримаємо:

.

 

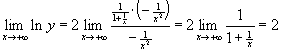Отже, . ^