§3 Поняття границі функції

3.1 Визначення границі функції

Нехай функція визначена на деякій підмножині множини дійсних чисел , і – гранична точка множини . Нагадаємо, що у будь-якому –околі граничної точкиміститься нескінченне число точок множини , проте сама точка може й не належати .

 

Визначення 1. (Гейне). Число називається границею функції при (або в точці ), якщо для довільної послідовності , збіжної до , відповідна послідовність значень функції збіжна до .

Якщо число– границя функції в точці , то пишуть або при .

Нехай функція має границю , тоді вона, очевидно, єдина. Це випливає з того, що збіжна послідовність може мати лише одну границю (див. гл.5, §1).

 

Визначення 2. (Коші). Число називається границею функції при (або в точці ), якщо для будь-якого можна знайти таке число , що при всіх , які задовольняють нерівність

виконується нерівність

Визначення границі функції в точці за Гейне і за Коші еквівалентні.

Відзначимо геометричний зміст визначення 2, скориставшись графіком функції (рис.40 ). Який би малий –окіл точки А не взяти, повинен існувати такий –окіл точки , що коли змінюється між і , графік функції знаходиться у смузі шириною між прямими . Підкреслимо, що в точці функція може набувати значення, яке не дорівнює А, або навіть бути невизначеною. Тому в визначенні 2 йдеться саме про нерівність 

 

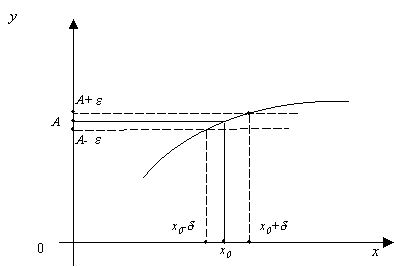
Рис.43

3.2 Односторонні границі

При дослідженні функції корисні поняття односторонніх границь.

 

Визначення 3 (Гейне). Число А називається правою (лівою) границею функції f(x) в точці х₀, якщо для довільної послідовності {x_n} X, x_n  x₀ (x_n  x₀) (n N), збіжної до х₀ , відповідна послідовність значень функції {f(x_n)} збіжна до А. При цьому вживають відповідно позначення

 f(x_n)=A  f(x_n)=A

або

f(x₀+0)=А (f(x₀-0)=А).

В окремому випадку, коли х₀=0, пишуть  f(x_n)=A  f(x_n)=A.

 

Визначення 4 (Коші). Число називається правою (лівою) границею функції в точці х₀ , якщо для будь-якого знайдеться таке число , що при всіх х, які задовольняють нерівностям

 ,

 

виконується нерівність

 

Визначення 3 і 4, звичайно ж, еквівалентні.

Зв’язок між односторонніми границями і границею функції встановлює теорема 3.

Теорема 3. Функція f(x) має границю в точці х₀ тоді й тільки тоді, коли існують їх права і ліва границі в цій точці, які збігаються між собою, при цьому

.

 

3.3 Границя функції на нескінченності і нескінченні границі

Нехай функція f(x) визначена при х х₀ (х х₀).

Визначення 5. Число А називається границею функції f(x) при х (х - ), якщо для будь-якого можна знайти таке , що при всіх х, які задовольняють нерівності , виконують нерівність

При цьому вживають відповідні позначення

 f(x)=A  f(x)=A

або

f(x) A, х + (f(x) A, х - ).

В разі, якщо існують границі функції f(x) як при х + , так і при х - , причому f(x)=f(x)=A, то вживають позначення

 f(x)=A або f(x) A, х 

Вище малося на увазі, що А – певне число. Іноді зручно розглядати нескінченні границі функції.

 

Визначення 6. Кажуть, що функція f(x) має своєю границею + (- ) при х х₀ (або в точці х₀), якщо для будь-якого Е>0 можна знайти таке число ?>0, що при всіх х, які задовольняють нерівність 0<|x-x₀|<, виконується нерівність f(x)>E (f(x)<-E).

При цьому вживають відповідно позначення

 f(x)=+ ( f(x)=- )

або

f(x) + х х₀      (f(x) -- , х х₀).

 

Аналогічно тому, як це зроблено в 3.2 цього параграфа, нескладно визначити також односторонні нескінченні границі

 f(x)=± ; f(x)=± .

 

Приклад 5. Використовуючи визначення, довести (3х-2)=1.

Візьмемо будь-яке число >0. Задача полягає в тому, щоб по цьому знайти таке    >0, при якому із нерівності |x-1|< випливала нерівність |f(x)-1|=|(3x-2)-1|< . Перетворюючи останню нерівність, отримаємо |(3x-1|<  або |x-1|<.

Отже, якщо взяти , то для всіх х, які задовольняють нерівності |x-1|< , виконується нерівність |f(x)-1|< . Це і означає, що =(3х-2)=1.

Якщо, наприклад, =1, то , якщо =, то , якщо =0,01, то 0,03 і т.д.; таким чином, залежить від . Тому в визначенні границі іноді пишуть = ().