§6 Скалярний добуток векторів

У фізичних, технічних економічних застосуваннях математики велике значення має розв‘язок задачі про визначення роботи, яку виконує задана стала сила при переміщенні матеріальної точки. Якщо точка переміщується прямолінійно, то, як відомо, робота дорівнює добутку величини сили на величину переміщення і на косинус кута між напрямком сили і напрямком переміщення. Позначимо силу , а переміщення , отримаємо для обчислення роботи вираз:

 

Оскільки подібна операція з двома векторами зустрічається досить часто, то для неї введена спеціальна назва, спеціальне позначення і вивчені всі нові властивості.

 

Визначення. Скалярним добутком двох векторів називається добуток їх довжин і косинуса кута між ними.

Скалярний добуток двох векторів і позначимо символом . У відповідності з визначенням

 (1)

 

Безпосередньо із визначення випливає, що скалярний добуток двох векторів є скаляр.

Кут між двома векторами не залежить від того, який вектор вибирається першим і який другим, тому

 (2),

 

тобто скалярний добуток має комутативну властивість.

Оскільки є проекція вектора на вісь, направлену так, як і вектор , є проекція вектора на вісь, направлену по вектору , то

 (3)

 

Тепер легко показати, що скалярний добуток векторів має розподільчу властивість, тобто

 (4)

 

Дійсно

 

Але .

 

Отже

.

 

Неважко перевірити, що скалярний добуток має асоціативну властивість по відношенню до скалярного множника.

 (5)

 

Із визначення скалярного добутку векторів випливає, що

 

Отже, скалярний добуток вектора на самого себе дорівнює квадрату довжини вектора. Зокрема

 (6)

Якщо два вектори взаємно перпендикулярні, то їх скалярний добуток дорівнює нулю. Навпаки, якщо скалярний добуток дорівнює нулю, але ні один із векторів не є нуль, то в нуль повинен обертатися косинус кута між векторами, а тому вектори повинні бути перпендикулярні.

 

Отже, для того щоб два вектори були перпендикулярні, необхідно і достатньо, щоб їх скалярний добуток дорівнював нулю.

Оскільки напрямок нульового вектора вважається довільним, то можна вважати нульовий вектор перпендикулярним будь-якому вектору. Тому в наведеній умові перпендикулярності двох векторів немає необхідності особливо вказувати, що ні один із векторів не повинен бути нульовим.

Із умови перпендикулярності отримаємо, зокрема, що

 (7)

Якщо вектори задані своїми координатами в ортонормованому базисі , то, використовуючи розподільчу і сполучну по відношенню до скалярного множника властивості скалярного добутку, одержимо:

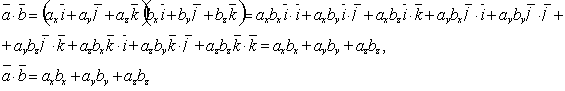 (8)

тобто скалярний добуток двох векторів дорівнює сумі добутків одноіменних координат цих векторів.

Із визначення скалярного добутку двох векторів безпосередньо знаходиться формула для обчислення косинуса кута між двома векторами

 (9)

 

§7 Векторний добуток векторів

Визначення. Векторним добутком двох векторів називається третій вектор, який має довжину, чисельно рівну площі паралелограма, що побудований на заданих векторах, перпендикулярний площині цих векторів і утворює з впорядкованою парою заданих векторів праву трійку.

Позначається векторний добуток заданих векторів і символом (іноді позначають .

 

Оскільки площа паралелограма, побудованого на векторах і , дорівнює добутку довжини цих векторів і синуса кута між ними, то

 (1)

 

Вкажемо на основні властивості векторного добутку векторів. Відмітимо передусім, що

 (2)

 

Дійсно, нехай

 

Оскільки

 і 

 

Вектори і перпендикулярні одній і тій же площині (площина, визначена векторами і ). Вектори , , утворюють праву трійку. Праву ж трійку утворюють і вектори , , `, тому вектори і мають однакові довжини, перпендикулярні одній і тій же площині і направлені в протилежні сторони. Це означає, що . Отже, при перестановці векторів, що перемножуються, напрямок векторного добутку змінюється на протилежний, а довжина не змінюється.

Можна довести, що векторний добуток двох векторів має сполучну властивість по відношенню до третього – скалярного – співмножника.

 (3)

 

і має розподільчу властивість:

 (4)

 

Із визначення векторного добутку векторів випливає, що векторний добуток колінеарних векторів є завжди нульовий вектор. Зокрема, завжди

.

 

Оскільки вектори , , взаємно перпендикулярні, мають одиничні довжини і утворюють праву трійку, то

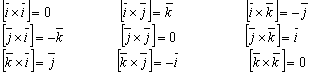 (5)

 

Використовуючи розподільчу і сполучну по відношенню до скалярного множника властивості векторного добутку, можна отримати формули для обчислення векторного добутку векторів, заданих шляхом розкладу по ортонормованому базису:

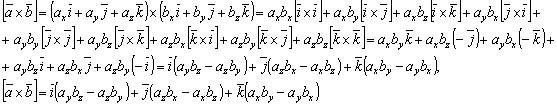 (6)

 

Важливою геометричною задачею, яка розв’язується з допомогою введеної операції, є обчислення площини трикутника по координатах його вершин.

Нехай задані координати вершин трикутника А, В, С. Знаючи їх, знаходимо і . Площа трикутника АВС дорівнює половині площі паралелограма, побудованого на векторах і . Отже,

 (7)

Приклад. А(1, -2,0); В(2, 1, -1); С(0, 3, 1). Знайти .

 

Розв’язок

 

Нарешті, формулу для обчислення векторного добутку векторів (6) зручніше записувати через визначник

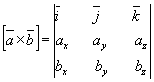 (8),

 

розкладаючи який по елементах першого рядка, отримаємо формулу (6).