
- •Конспект лекцій з курсу
- •§2 Визначники матриць другого порядку
- •§3. Визначники матриць третього порядку
- •§ 4 Визначники матриць вищих порядків
- •Приклади розв’язання задач
- •§5 Розв'язок систем n рівнянь із n невідомими
- •5.1. Правило Крамера
- •5.2. Розв'язок і дослідження систем рівнянь першого порядку методом повного виключення (Метод Гаусса).
- •1. Система однорідних рівнянь 1-ого порядку завжди сумісна.
- •2. Якщо визначник системи однорідних рівнянь 1-ого порядку дорівнює нулю, тоді система має нескінченну множину розв 'язків.
- •§ 6 Ранг матриці, теорема про сумісність систем рівнянь першого порядку
- •Іі. Приклади розв`язку задач
- •Обчислення рангу матриці методом облямування
- •§ 7 Основні операції з матрицями
- •Приклади розв`язку задач
- •§ 8 Обернена матриця, розв`язок матричних рівнянь
- •Іі. Приклади розв`язку задач
- •§9. Модель багатогалузевої економіки
- •Глава іі: Векторна алгебра
- •§1 Основні поняття
- •§2 Лінійні операції з векторами.
- •§ 3 Лінійна залежність та лінійна незалежність системи векторів
- •Приклади розв‘язку задач
- •§4 Проекція вектора на ось
- •§5 Прямокутна декартова система координат в просторі
- •§6 Скалярний добуток векторів
- •§7 Векторний добуток векторів
- •§8 Мішаний добуток векторів
- •Іі. Приклади розв’язку задач
- •Глава ііі: Аналітична геометрія
- •§1 Відповідність між геометричними образами та рівняннями
- •§ 2 Лінійні образи - площина і пряма
- •§ 3 Лінії другого порядку
- •Приклади розв`язку задач
- •§4 Перетворення координат на площині. Застосування перетворення координат до спрощення рівнянь кривих другого порядку.
- •§5 Циліндричні поверхні з твірними, паралельними координатним осям; поверхні другого порядку
- •5.1. Дослідження форми еліпсоїда
- •5.2. Дослідження форми однопорожнинного гіперболоїда
- •5.3. Дослідження формули двопорожнинного гіперболоїда
- •5.4. Дослідження формули еліптичного параболоїда
- •5.5. Дослідження форми гіперболічного параболоїда
- •6. Дослідження форми конуса 2-го порядку
- •Приклади розв`язку задач
- •§6 Полярна система координат на площині. Циліндрична і сферична системи координат в просторі
- •6.1. Полярна система координат на площині
- •6.2. Циліндрична система координат
- •6.3. Сферична система координат
- •Приклади розв’язку задач
- •Розділ іі. Вступ до математичного аналізу
- •Глава IV: Функції
- •§1 Поняття множини
- •§2. Абсолютна величина дійсного числа
- •§3. Поняття функції
- •§4 Застосування функцій в економіці
- •Розв’язок задач
- •Глава V: Границя і неперервність
- •§1 Поняття границі послідовності
- •1.1 Збіжні послідовності
- •1.2 Нескінченно малі і нескінченно великі.
- •§2 Основні властивості збіжних послідовностей
- •§3 Поняття границі функції
- •3.1 Визначення границі функції
- •3.2 Односторонні границі
- •3.3 Границя функції на нескінченності і нескінченні границі
- •§4 Властивості границь
- •§5 Перша і друга важливі границі
- •5.1 Перша важлива границя
- •5.2 Друга важлива границя
- •Задача про неперервне нарахування процентів
- •§6 Нескінченно малі та нескінченно великі функції
- •§7 Неперервність функції
- •Розв’язки задач
- •Розділ ііі. Диференціальне числення
- •Главаvi: Похідні та диференціали
- •§ 1 Поняття похідної
- •§2 Зміст похідної
- •2.1. Задача про дотичну до кривої
- •2.2. Задача про миттєву швидкість
- •2.3. Задачі про витрати виробництва та виручку
- •§3. Правила диференціювання
- •3.1 Диференціювання суми, добутку й частки
- •3.2. Диференціювання складної функції
- •§4. Диференційованість елементарних функцій
- •§5. Похідні вищих порядків
- •§ 6. Диференціал функції
- •§ 7. Диференціали вищих порядків
- •§8 Розв'язки задач
- •§ 9 Економічний зміст похідної.
- •Глава 7: Застосування похідних до дослідження функцій
- •§ 1 Загальні властивості функцій, неперервних на замкненому проміжку
- •§ 2 Теореми про середнє значення
- •§ 3 Правила Лопіталя
- •§4 Дослідження функцій
- •4.1. Умови монотонності функцій
- •4.3. Знаходження найменшого й найбільшого значень
- •4.4 Опуклість, угнутість та точки перегину кривої
- •3.5. Асимптоти. Дослідження графіка функції в цілому
- •§ 5 Застосування похідної в економічній теорії.
- •§ 5. Розв’язки задач
Глава іі: Векторна алгебра
§1 Основні поняття
Розглядаючи різні процеси та явища, ми зустрічаємося з об‘єктами та величинами різної природи. Деякі із фізичних величин – такі як маса, температура, об‘єм, потенціал характеризуються одним числом. Вони називаються скалярними величинами або просто скаляром. Поряд зі скалярами існують величини, для характеристики яких необхідно вказати також і напрямок. Такі, наприклад, сила, швидкість, переміщення, напруження та інші. Ці фізичні величини називаються векторними величинами або векторами.
Геометричною моделлю векторної величини являється прямолінійний відрізок із вибраним на ньому напрямком.
В нашому курсі ми і будемо мати справу в основному з цією моделлю, а тому прямолінійний відрізок, для якого вказано, яка із обмежуючих його точок вважається початком, яка кінцем, будемо називати геометричним вектором або просто вектором.
Якщо А –
початок вектора, В –
його кінець, тоді сам вектор будемо
позначати символом ![]() .
Символ
.
Символ ![]() буде,
очевидно, позначати вектор, початок
якого знаходиться в точці В,
а кінець - в точціА.
Під довжиною вектора будемо розуміти
відстань між початком і кінцем вектора.
Довжину, або, як часто говорять, модуль
вектора
буде,
очевидно, позначати вектор, початок
якого знаходиться в точці В,
а кінець - в точціА.
Під довжиною вектора будемо розуміти
відстань між початком і кінцем вектора.
Довжину, або, як часто говорять, модуль
вектора ![]() ,
позначають символом
,
позначають символом ![]() .
Очевидно, вектори
.
Очевидно, вектори ![]() і
і ![]() мають
однакову довжину (тобто
мають
однакову довжину (тобто ![]() =
=![]() )
і протилежні напрямки.
)
і протилежні напрямки.
Вище було вказано, що вектор повністю визначається своїм початком та кінцем. Він може бути заданий також початком, довжиною та напрямком. Але для цілого ряду питань точка прикладання (початок вектора) не обов‘язкова – має значення лише довжина вектора та його напрямок. Такі вектори називаються вільними. Оскільки точка прикладання (початок вектора) будь-яка, тоді вектор можна переносити, зберігаючи його довжину і напрямок, в будь-яку точку простору. А тому вектори, які мають рівні довжини та однакові напрямки, називаються рівними векторами. Тобто,вектори рівні, якщо при паралельному переносі векторів і співпаданні їх початків будуть співпадати і їх кінці.
Оскільки
для вільних векторів можна не вказувати
початок, тоді вони часто визначаються
одною буквою: вектор ![]() ,
вектор
,
вектор ![]() і
т.д. Довжина вектора
і
т.д. Довжина вектора ![]() позначається
символом
позначається
символом ![]() .
.
Введемо ще три терміни, які часто зустрічаються у векторній алгебрі.
Колінеарними називаються вектори, які лежать на паралельних прямих. Або, вектори колінеарні, якщо при паралельному їх переносі та співставленні їх початків вони лежать на одній прямій.
Компланарними називаються вектори, які лежать на паралельних площинах. Тобто, вектори компланарні, якщо при паралельному їх переносі і співставленні початків вони лежать в одній площині. Очевидно, що два вектори завжди компланарні.
Нульовим вектором
являється вектор, у якого початок
співпадає з кінцем. Довжина нульового
вектора дорівнює нулю, а напрямок
довільний, а тому нульовий вектор можна
вважати колінеарним будь-якому іншому
вектору. Позначати нульовий вектор
будемо символом ![]() .
.
§2 Лінійні операції з векторами.
Вводячи різні операції з векторами, збережемо прийняті в алгебрі чисел терміни “додавання” та “множення”. Але необхідно взяти до уваги, що оскільки поняття “вектор” та “число” суттєво різні, тоді і зміст вказаних операцій може не співпадати з відповідними операціями алгебри чисел. А тому необхідно дослідити основні правила цих по суті нових операцій та перевірити виконання встановлених в алгебрі чисел законів: комутативного, асоціативного та дистрибутивного.
Визначення. Сумою двох векторів називається третій вектор, початок якого є початком 1-го вектора, кінцем – кінець 2-го, при чому початок 2-го вектора співставлений з кінцем 1-го.
Із введеного визначення випливає, що при додаванні векторів має місце комутативна властивість, тобто
![]() (1)
(1)
Дійсно,
доповнимо трикутник, складений із
векторів ![]() ,
, ![]() ,
, ![]() до
паралелограма (рис.3). Оскільки
до
паралелограма (рис.3). Оскільки ![]() ,
, ![]() і
згідно визначення суми векторів
і
згідно визначення суми векторів ![]() і
і ![]() ,
тоді
,
тоді ![]() .
.
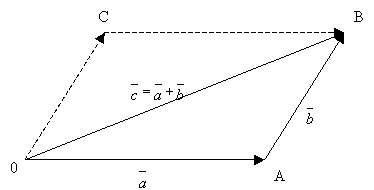
Рис.3
Із
наведених міркувань випливає, що суму
двох векторів ![]() і
і ![]() можна
визначити як діагональ паралелограма,
побудованого на векторах
можна
визначити як діагональ паралелограма,
побудованого на векторах ![]() і
і ![]() ,
які виходять із загального початку
заданих векторів.
,
які виходять із загального початку
заданих векторів.
Легко перевірити, що при додаванні векторів має місце асоціативна властивість, тобто
![]() (2)
(2)
а
тому суму трьох векторів можна записати
просто у вигляді ![]() .
Дійсно, побудуємо із векторів
.
Дійсно, побудуємо із векторів ![]() і
і ![]() вектор
вектор ![]() ;
побудуємо також суму векторів
;
побудуємо також суму векторів ![]() та
вектора
та
вектора ![]() (рис.4).
(рис.4).

Відмічений
пунктиром вектор ![]() згідно
визначення і є сумою векторів
згідно
визначення і є сумою векторів ![]() і
і ![]() ,
, ![]() .
Разом з тим
.
Разом з тим ![]() ,
таким чином,
,
таким чином, ![]() .
.
Проведені
міркування дають прийом додавання
будь-якого числа векторів. Нехай
задані k векторів ![]() ,
і необхідно знайти їх суму. До кінця
вектора
,
і необхідно знайти їх суму. До кінця
вектора ![]() прикладемо
початок вектора
прикладемо
початок вектора ![]() ,
до кінця побудованого вектора
,
до кінця побудованого вектора ![]() приставимо
початок вектора
приставимо
початок вектора ![]() і
т.д. Нарешті, до кінця вектора
і
т.д. Нарешті, до кінця вектора ![]() приставимо
початок вектора
приставимо
початок вектора ![]() (рис.5).
(рис.5).

Тоді
вектор ![]() ,
початком якого є початок вектора
,
початком якого є початок вектора ![]() ,
а кінцем – кінець вектора
,
а кінцем – кінець вектора ![]() ,
і буде сумою векторів
,
і буде сумою векторів ![]() :
: ![]() .
При цьому байдуже, в якому порядку
нумеруються задані вектори.
.
При цьому байдуже, в якому порядку
нумеруються задані вектори.
Таким чином, сума декількох векторів представляє собою вектор, який замикає ламану, побудовану на заданих векторах. Може статися, що кінець останнього вектора співпаде з початком першого, і, отже, у замикаючого вектора кінець співпаде з початком. В цьому випадку сума векторів є нульовим вектором.
Визначення. Добутком
вектора ![]() на
число
на
число ![]() (або
числа
(або
числа ![]() на
вектор
на
вектор ![]() )
називається вектор
)
називається вектор ![]() ,
довжина якого в
,
довжина якого в ![]() раз
більше довжини вектора
раз
більше довжини вектора ![]() і
напрямок співпадає з напрямком вектора
і
напрямок співпадає з напрямком вектора ![]() ,
якщо
,
якщо ![]() ,
та протилежний напрямку
,
та протилежний напрямку ![]() ,
якщо
,
якщо ![]() .
.
Оскільки
ділення на число ![]() представляє
собою множення на число
представляє
собою множення на число ![]() ,
то можна виконувати і ділення вектора
на відмінне від нуля число.
,
то можна виконувати і ділення вектора
на відмінне від нуля число.
Нехай ![]() ненульовий
вектор. Оскільки
ненульовий
вектор. Оскільки ![]() -
додатне число, тоді вектор
-
додатне число, тоді вектор 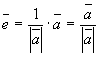 направлений
так, як і вектор
направлений
так, як і вектор ![]() .
Довжина вектора
.
Довжина вектора ![]() дорівнює,
очевидно, 1. Вектор
дорівнює,
очевидно, 1. Вектор ![]() ,
який має довжину рівну 1 і направлений
так, як і вектор
,
який має довжину рівну 1 і направлений
так, як і вектор ![]() ,
називається ортом вектора
,
називається ортом вектора ![]() .
.
Добуток
вектора ![]() на
число –1 (або, що теж саме, добуток числа
–1 на вектор
на
число –1 (або, що теж саме, добуток числа
–1 на вектор ![]() ),
тобто вираз
),
тобто вираз ![]() (або
(або ![]() ),
записують як -
),
записують як -![]() .
Оскільки вектори
.
Оскільки вектори ![]() та
та ![]() мають
у відповідності з визначенням однакові
довжини та протилежні напрямки, тоді
мають
у відповідності з визначенням однакові
довжини та протилежні напрямки, тоді
![]() (3)
(3)
Як
і в алгебрі чисел, в алгебрі векторів
немає потреби розглядати окремо дію
віднімання. Відняти від
вектора ![]() вектор
вектор ![]() означає
додати до вектора
означає
додати до вектора ![]() вектор
-
вектор
-![]() :
: ![]() .
А тому у векторних рівностях вектори
можна переносити із однієї частини
рівності в другу, змінюючи знак, який
стоїть перед вектором, на протилежний.
Тобто, якщо
.
А тому у векторних рівностях вектори
можна переносити із однієї частини
рівності в другу, змінюючи знак, який
стоїть перед вектором, на протилежний.
Тобто, якщо ![]() ,
тоді
,
тоді ![]() .
.
Неважко переконатись, що при множенні вектора на число має місце асоціативна та дистрибутивна властивості. Покажемо, по-перше , що
![]() (4)
(4)
(тобто має місце асоціативна властивість по відношенню до числових множників).
Дійсно,
оскільки довжина вектора ![]() дорівнює
дорівнює ![]() ,
довжина вектора
,
довжина вектора ![]() дорівнює
дорівнює ![]() та
довжина вектора
та
довжина вектора ![]() дорівнює
дорівнює ![]() ,
тоді довжина векторів
,
тоді довжина векторів ![]() та
та ![]() однакова.
Далі, якщо, наприклад, числа
однакова.
Далі, якщо, наприклад, числа ![]() та
та ![]() додатні,
тоді вектори
додатні,
тоді вектори![]() ,
, ![]() ,
, ![]() направлені
так, як і вектор
направлені
так, як і вектор ![]() ,
а тому усі вони мають однакові напрямки.
Якщо
,
а тому усі вони мають однакові напрямки.
Якщо ![]() та
та ![]() ,
тоді вектори
,
тоді вектори ![]() ,
, ![]() ,
, ![]() направлені
всі протилежно вектору
направлені
всі протилежно вектору ![]() ,
а тому також однаково направлені.
,
а тому також однаково направлені.
Аналогічні міркування проводяться і у всіх інших випадках.
Доведемо тепер, що
![]() (5)
(5)
нехай ![]() (рис.
6 при
(рис.
6 при ![]() та
рис.7 при
та
рис.7 при ![]() ).
).
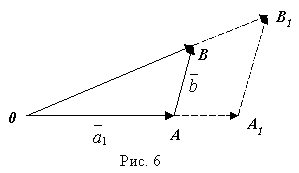

Оскільки ![]() ,
тоді кути ОАВ та ОА1В1 рівні.
Оскільки
,
тоді кути ОАВ та ОА1В1 рівні.
Оскільки ![]() ,
тоді трикутники ОАВ та ОА1В1 подібні.
Звідси, точки О,
В, В1 лежать
на одній прямій і
,
тоді трикутники ОАВ та ОА1В1 подібні.
Звідси, точки О,
В, В1 лежать
на одній прямій і ![]() ,
а тому
,
а тому ![]() .
Але
.
Але ![]() і
твердження доведене.
і
твердження доведене.
Очевидно, має місце також співвідношення
![]() (6)
(6)
Розглянуті операції – додавання векторів та множення вектора на число – називаються лінійними операціями, а вектор
![]() (7),
(7),
отриманий
в результаті проведення декількох
лінійних операцій, лінійною комбінацією
векторів ![]() .
Числа
.
Числа ![]() називаються
коефіцієнтами цієї лінійної комбінації.
називаються
коефіцієнтами цієї лінійної комбінації.
