Обратная матрица

Пусть - квадратная матрица порядка. Матрицаназываетсяобратной матицейк матрице, если выполняются равенства, где‑ единичная матрица порядка.

Теорема 1. Если для данной матрицы существует обратная матрица, то она единственная.

Пусть и‑ матрицы, обратные к матрице. Тогда, с другой стороны,.

Откуда . Обратную матрицу к матрицеобозначают.

Теорема 2. Матрица имеет обратную матрицу тогда и только тогда, когда.

Пусть имеет обратную матрицу. Тогдаи, применяя теорему об умножении определителей, получаемили. Следовательно,.

Пусть . Укажем явное выражение матрицычерез элементы матрицы, а именно: если, то:

,

(9.5)

здесь ‑ алгебраическое дополнение к элементу. Матрица (9.5) получается из матрицыследующим образом. Сначала вместо каждого элементапишется его алгебраическое дополнение, затем полученная матрица транспонируется и получается т.н. присоединенная матрица. Для получения обратной матрицы присоединенная матрица умножается на величину, обратную.

Непосредственное умножение на матрицу (9.5) слева и справа дает единичную матрицу, что подтверждает, что (9.5) – матрица, обратная к.

Пример 12.Найти обратную матрицу к матрице.

Так как , тосуществует. Вычислим алгебраические дополнения элементов матрицы:

,	,
,	,
,	,
,	,
.

Матрицу находим в два приема, согласно формуле (9.5). Сначала запишем матрицу, состоящую из алгебраических дополнений элементов.Затем матрицатранспонируется и умножается на число обратное, в данном случае – на (-1). Окончательно получаем:

.

Матрица называется неособеннойилиневырожденной, если ее определитель не равен нулю. Отметим свойства обратных матриц. Еслии‑ невырожденные матрицы одинакового порядка, то:

,

,

,

.

Контрольные вопросы к лекции №9

1. Понятие матрицы.

2. Виды матриц.

3. Понятие транспонирования матриц.

4. Операции сложения и вычитания матриц.

5. Операции умножения и возведения в степень матриц.

6. Понятие определителя.

7. Определитель - го порядка.

8. Правила нахождения определителей 2 и 3 порядка.

9. Свойства определителей.

10. Правила нахождения определителей - го порядка.

11. Понятие обратной матрицы.

12. Схема нахождения обратной матрицы.

13. Понятие ранга матрицы.

Лекция 10. Понятие линейного оператора

Основные понятия:

матрица перехода; линейное преобразование; собственное значение матрицы; собственный вектор матрицы; диагонализация матрицы; ортогональная матрица; характеристический многочлен.

Переход к новому базису

Пусть в пространстве R имеются два базиса: старый и новый. Каждый из векторов нового базиса можно выразить в виде линейной комбинации векторов старого базиса:

Полученная система означает, что переход от старого базиса к новому задается матрицей перехода:

,

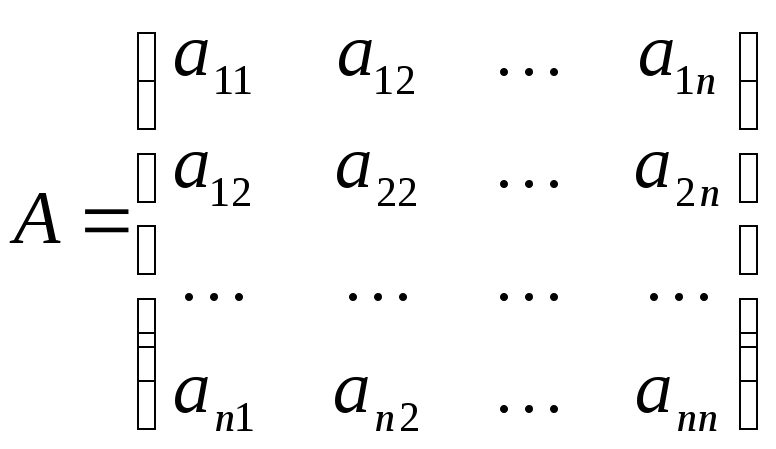причем, коэффициенты разложения новых базисных векторов по старому базису образуют столбцы этой матрицы.

Матрица — неособенная, так как в противном случае ее столбцы (а следовательно, и базисные векторы) оказались бы линейно зависимыми. Обратный переход от нового базисак старому базисуосуществляется с помощью обратной матрицы.

Найдем зависимость между координатами вектора в разных базисах. Пусть рассматриваемый вектор имеет координатыотносительно старого базиса и координатыотносительно нового базиса, т.е.:

Подставив значения из системы в левую часть этого равенства, получим после преобразований:

т.е. в матричной форме: или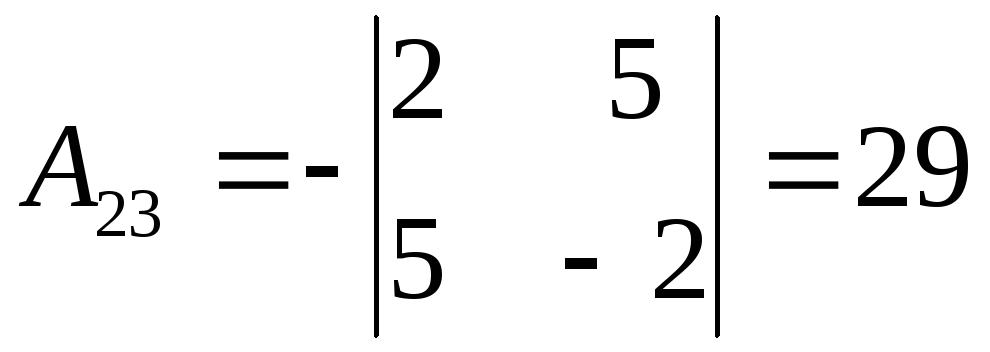