Исследование на плоскости уравнения второй степени

Рассмотрим уравнение:

(7.9)

где среди коэффициентов есть отличные от нуля, т.е. (7.9) –уравнение второй степениотносительнои.

Возьмем на плоскости две прямоугольные системы координат: , которую будем называть старой, и новую, полученную изповоротом ее вокруг начала координат на угол,.

Старые координаты выражаются через новые координатыпо формулам:

(7.10)

Подставив выражения для ив уравнение (8), получим:

(7.11)

Это уравнение в системе координат задает ту же линию, что и уравнение (7. 9) в системе.

Если в уравнении (7.9) , то за счет выбора углав (7.10) можно добиться того, что. Для этого уголнадо взять таким, чтобы. Поэтому будем считать, тогда уравнение (7.11) примет вид:

(7.12)

Преобразуя это уравнение и применяя параллельный перенос координатных осей, придем к уравнению:

(7.13)

В зависимости от знаков коэффициентов уравнения (7.13) рассмотрим следующие случаи:

1. , тогда уравнение (7.13) примет вид, где. Этоуравнение эллипса.

2. , то, обозначив_,имеем. Этому уравнению не удовлетворяет ни одна точка с координатами. Следовательно, это уравнение задаетпустое множество.

3. . Обозначаяприведем уравнение (12) к виду. Этоуравнение гиперболы.

4. Случаи ,,новых результатов не дают.

5. . Тогда уравнение (7.13) можно привести к виду. Это уравнение задает пару прямых, пересекающихся в начале координат.

Рассматривая далее методично все случаи, придем к выводу: уравнение вида (7.9) задает одну из следующих фигур: эллипс, гиперболу, параболу, пару пересекающихся прямых, пару параллельных прямых, прямую, точку или пустое множество.

Контрольные вопросы к лекции №7

1. Понятие кривых второго порядка: эллипса, гиперболы, параболы.

2. Уравнение эллипса, каноническое уравнение эллипса.

3. Понятия фокусов эллипса; фокальных радиусов; директрисы и эксцентриситета эллипса.

4. Каноническое уравнение гиперболы.

5. Фокусы и фокальные радиусы гиперболы, асимптота гиперболы.

6. Каноническое уравнение параболы.

7. Приведение уравнения второй степени к каноническому виду.

Тема 3. Линейная алгебра Лекция 8. Понятие евклидова пространства

Основные понятия:

евклидово пространство; –мерный вектор; неравенство Коши-Буняковского; коллинеарные векторы; неколлинеарные векторы; сонаправленные векторы; противоположно направленные векторы; линейная комбинация векторов; линейно зависимые векторы; линейно независимые векторы; размерность линейного пространства; базис векторного пространства.

N-мерные векторы

Декартово произведение множества действительных чисел само на себя состоит из всевозможных упорядоченных числовых пар. Это множество обозначаюти его можно отождествить с плоскостью. Множествосостоит из упорядоченных троек и представляет собой трехмерное пространство. Если осуществить декартово произведениена себяраз, можно получить множество всех точек-мерного пространства. Каждый элемент пространствапредставляет собой последовательностьчисел и записывается в виде. Числоназывается первой координатой-мерного вектора,– второй координатой и т.д., а число– размерностью вектора. В ряде случаев в пространстве –мерных векторов также бывает возможно определить операцию скалярного произведения векторовичерез операции над их координатами.

В общем случае и– это–мерные векторы, т.е., и. Их скалярное произведение равно сумме попарных произведений их соответствующих координат, т.е.. Длиной–мерного вектораназывается число. Скалярное произведениеназывается скалярным квадратом вектораи обозначается. Поскольку скалярный квадрат является суммой квадратов координат вектора, то его значение будет неотрицательным, причемтогда и только тогда, когда все координаты этого вектора равны нулю, т.е. вектор– нулевой.

Пространство –мерных векторов, в котором определена операция скалярного произведения, называетсяевклидовым пространством.

Теорема.Если и– это–мерные векторы евклидова пространства, то справедливо неравенство:

Доказательство: Рассмотрим вектор, где– любое действительное число. Поскольку, то на основании свойств скалярного произведения можно записать:

Если предположить, что , то справедливо следующее:

Доказанное неравенство называется неравенством Коши-Буняковского.Причем, равенство имеет место тогда и только тогда, когда векторыилинейно зависимы. В общем случае, угол между векторамииможно определить как решение уравнения:

.

Таким образом, в евклидовом пространстве –мерных векторов скалярное произведение любых двух векторовиравно:

.

Теорема.Ненулевые –мерные векторыиравны тогда и только тогда, когда угол между этими векторами равен нулю и длины их равны.

Доказательство:

Необходимость:

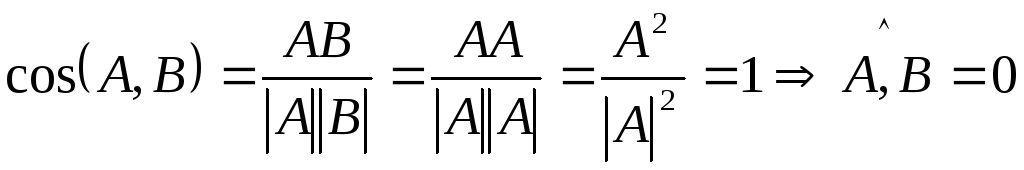
Достаточность:

Пусть и