- •Академия управления при Президенте Республики Беларусь
- •Содержание
- •Тема 1. Элементарная математика 13
- •Тема 2. Аналитическая геометрия 38
- •Тема 3. Линейная алгебра 81
- •Введение Лекция 1. Основы математической логики
- •Высказывания и логические связки
- •Контрольные вопросы к лекции №1
- •Тема 1. Элементарная математика Лекция 2. Элементы теории множеств
- •Основные понятия
- •Основные операции над множествами
- •Отображения
- •Отношения эквивалентности и упорядоченности
- •Контрольные вопросы к лекции №2
- •Лекция 3. Числовые множества
- •Основные понятия
- •Соединения. Бином Ньютона
- •Комплексные числа
- •Операции над комплексными числами
- •Формула Муавра. Извлечение корня из комплексного числа
- •Контрольные вопросы к лекции №3
- •Тема 2. Аналитическая геометрия Лекция 4. Векторы
- •Основные понятия
- •Линейные операции над векторами
- •Проекция вектора на ось
- •Линейная зависимость векторов
- •Базис. Координаты вектора в базисе
- •Декартовы прямоугольные координаты в пространстве. Координаты точек. Координаты векторов. Деление отрезка в данном отношении
- •Направляющие косинусы
- •Скалярное произведение
- •Векторное произведение
- •Смешанное произведение
- •Контрольные вопросы к лекции №4
- •Лекция 5. Прямая
- •Основные понятия
- •Взаимное расположение прямых
- •Контрольные вопросы к лекции №5
- •Лекция 6. Плоскость
- •Основные понятия
- •Нормальное уравнение плоскости
- •Взаимное расположение плоскостей
- •Контрольные вопросы к лекции №6
- •Лекция 7. Кривые второго порядка
- •Уравнение фигуры
- •Гипербола
- •Парабола
- •Исследование на плоскости уравнения второй степени
- •Контрольные вопросы к лекции №7
- •Тема 3. Линейная алгебра Лекция 8. Понятие евклидова пространства
- •Коллинеарные векторы
- •Размерность и базис векторного пространства
- •Контрольные вопросы к лекции №8
- •Лекция 9. Матрицы
- •Основные понятия
- •Операции над матрицами
- •Определитель матрицы
- •Ранг матрицы
- •Обратная матрица
- •Контрольные вопросы к лекции №9
- •Лекция 10. Понятие линейного оператора
- •Переход к новому базису
- •Линейное преобразование переменных
- •Собственные значения и собственные вектора матриц
- •Контрольные вопросы к лекции №10
- •Лекция 11. Многочлены
- •Основные понятия
- •Теорема о делении с остатком
- •Теорема Безу
- •Контрольные вопросы к лекции №11
- •Лекция 12. Квадратичные формы
- •Понятие квадратичной формы
- •Канонический базис квадратичной формы
- •Канонический базис из собственных векторов матрицы квадратичной формы
- •Канонический базис Якоби квадратичной формы
- •Положительно и отрицательно определенные квадратичные формы
- •Применение квадратичных форм к исследованию кривых второго прядка
- •Контрольные вопросы к лекции №12
- •Лекция 13. Системы линейных уравнений
- •Основные понятия
- •Критерий совместности системы линейных уравнений
- •Правило Крамера решения систем линейных уравнений
- •Метод Гаусса
- •Однородные системы уравнений
- •Разрешенные системы линейных уравнений
- •Контрольные вопросы к лекции №13
- •Лекция 14. Основы линейного программирования
- •Линейное программирование
- •Задача линейного программирования
- •Приведение общей задачи линейного программирования к канонической форме
- •Множества допустимых решений
- •Опорное решение задачи линейного программирования, его взаимосвязь с угловыми точками
- •Симплекс-метод с естественным базисом
- •Симплексный метод с искусственным базисом (м-метод)
- •Теория двойственности
- •Теоремы двойственности
- •Контрольные вопросы к лекции 14
- •Экзаменационные вопросы
- •Литература
- •Высшая математика
- •Часть I
- •220007, Г. Минск, ул. Московская, 17.
Направляющие косинусы
Пусть
дан вектор
![]() .
Единичный вектор того же направления,
что и
.
Единичный вектор того же направления,
что и![]() (орт вектора
(орт вектора![]() )
находится по формуле:
)
находится по формуле:
 .
.
Пусть
ось
![]() образует с осями координат углы
образует с осями координат углы![]() .Направляющими косинусами оси
.Направляющими косинусами оси
![]() называются косинусы этих углов:
называются косинусы этих углов:![]() .
Если направление
.
Если направление![]() задано единичным вектором
задано единичным вектором![]() ,
то направляющие косинусы служат его
координатами, т.е.:
,
то направляющие косинусы служат его
координатами, т.е.:
![]() .
.
Направляющие косинусы связаны между собой соотношением:
![]() .
.
Если
направление
![]() задано произвольным вектором
задано произвольным вектором![]() ,
то находят орт этого вектора и, сравнивая
его с выражением для единичного вектора
,
то находят орт этого вектора и, сравнивая
его с выражением для единичного вектора![]() ,
получают:
,
получают:

Скалярное произведение
Скалярными
произведением![]() двух векторов
двух векторов![]() и
и![]() называется число, равное произведению
их длин на косинус угла между ними:
называется число, равное произведению
их длин на косинус угла между ними:![]() .
.
Скалярное произведение обладает следующими свойствами:
 ;
; ;
;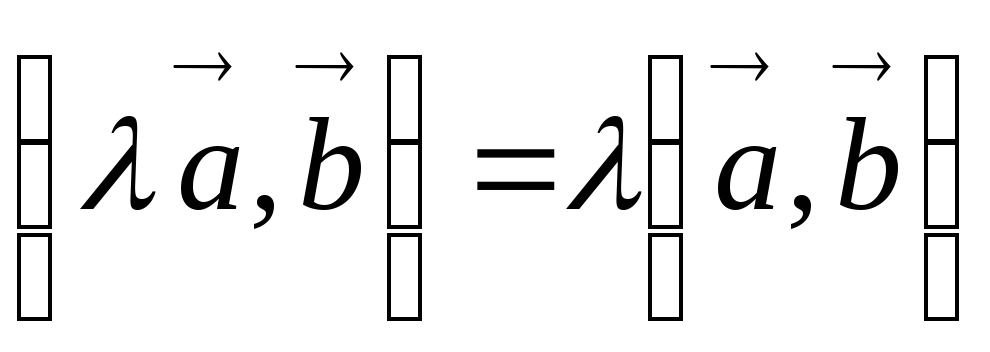 ;
;Если
 и
и ‑ ненулевые векторы, то
‑ ненулевые векторы, то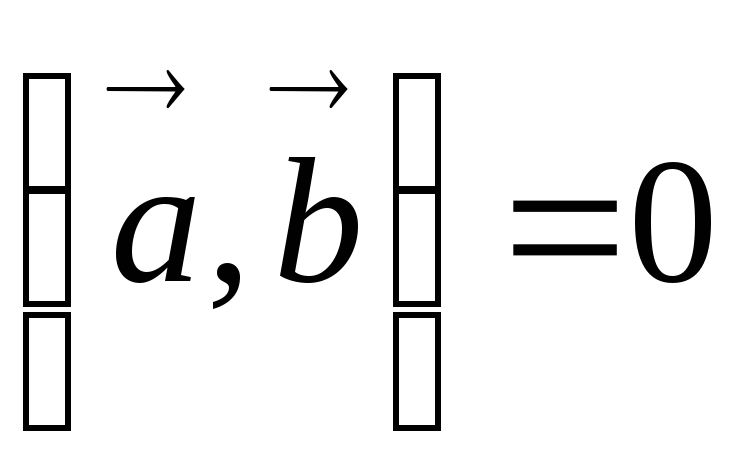 тогда
и только тогда, когда эти векторы
перпендикулярны. Если
тогда
и только тогда, когда эти векторы
перпендикулярны. Если ,
то угол между
,
то угол между и
и - острый, если
- острый, если ,
то угол - тупой;
,
то угол - тупой;Скалярный квадрат вектора
 равен квадрату его длины, т.е.
равен квадрату его длины, т.е. .
.
Следовательно,
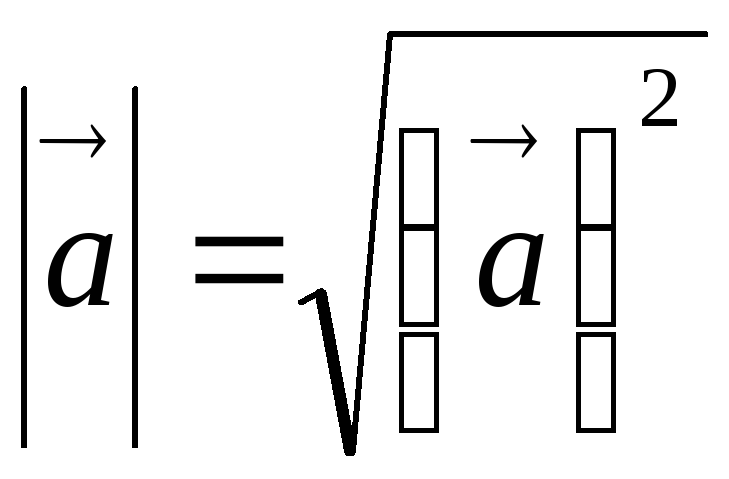 .
.
Геометрический
смысл скалярного произведения:
скалярное произведение вектора на
единичный вектор![]() равно проекции вектора
равно проекции вектора![]() на направление, определяемое
на направление, определяемое![]() ,
т.е.
,
т.е. .
.
Из
определения скалярного произведения
вытекает следующая таблица умножения
ортов
![]() :
:
![]()
![]() .
.
Если
векторы заданы своими координатами
![]() и
и![]() ,
т.е.
,
т.е.![]() ,
,![]() ,
то, перемножая эти векторы скалярно и
используя таблицу умножения ортов,
получим выражение скалярного произведения
,
то, перемножая эти векторы скалярно и
используя таблицу умножения ортов,
получим выражение скалярного произведения через координаты векторов:
через координаты векторов:
 .
.
Векторное произведение
Векторным
произведением вектора![]() на вектор
на вектор![]() называется вектор
называется вектор ,
длина и направление которого определяется
условиями:
,
длина и направление которого определяется
условиями:
 ,
где
,
где ‑ угол между
‑ угол между и
и ;
; перпендикулярен каждому из векторов
перпендикулярен каждому из векторов и
и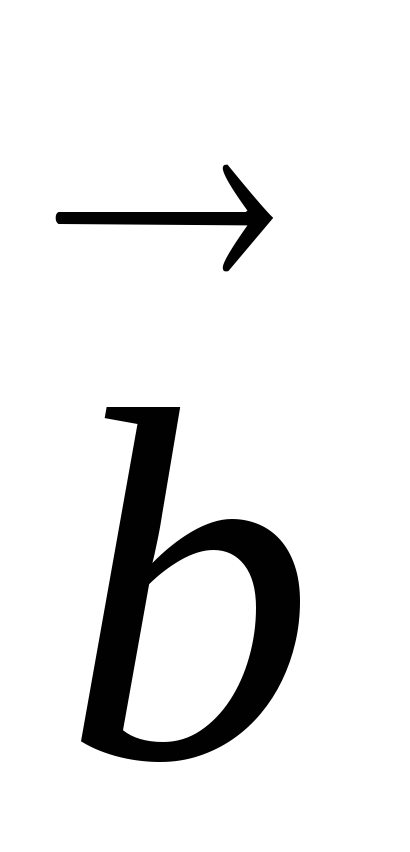 ;
; направлен так, что кратчайший поворот
от
направлен так, что кратчайший поворот
от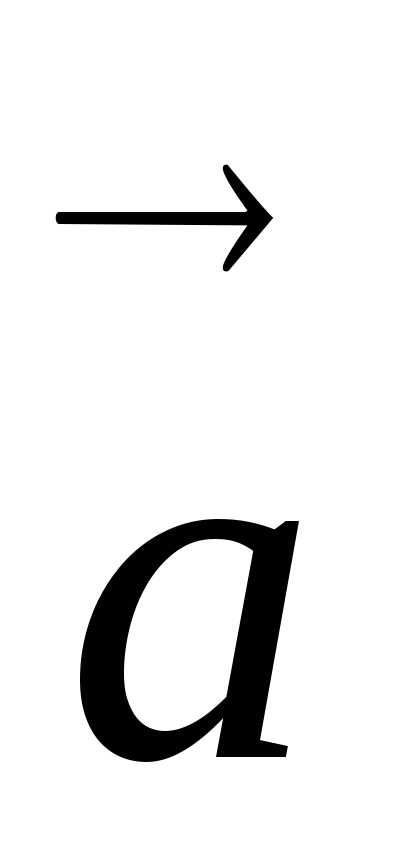 к
к виден из его конца совершающимся
против часовой стрелки.
виден из его конца совершающимся
против часовой стрелки.
Векторное произведение обладает следующими свойствами:
 ;
;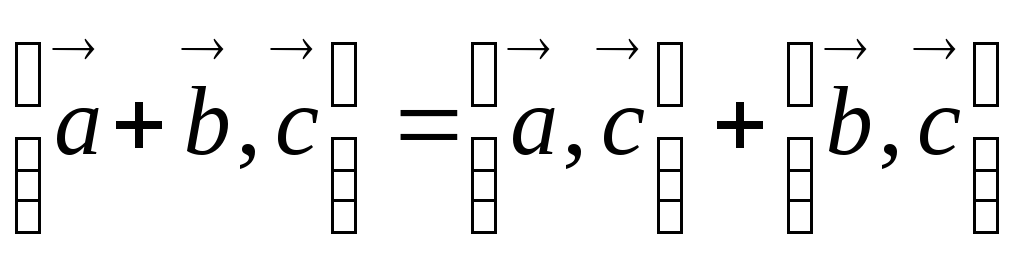 ;
; ;
;Векторное произведение равно нулю (нуль вектору) тогда и только тогда, когда
 и
и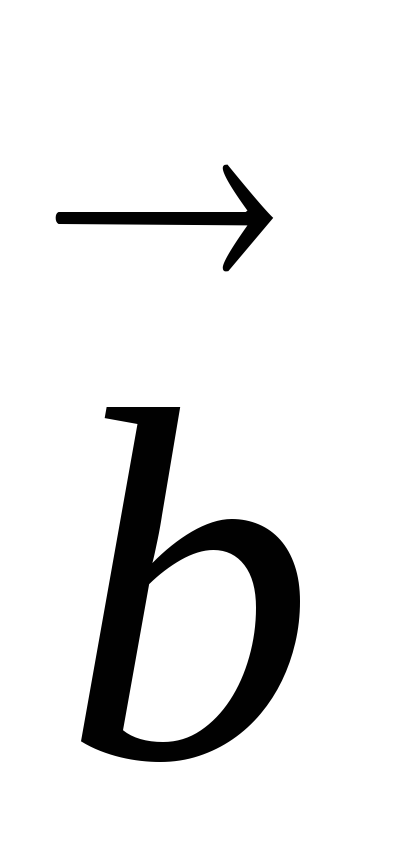 коллинеарны. В частности,
коллинеарны. В частности, для любого вектора
для любого вектора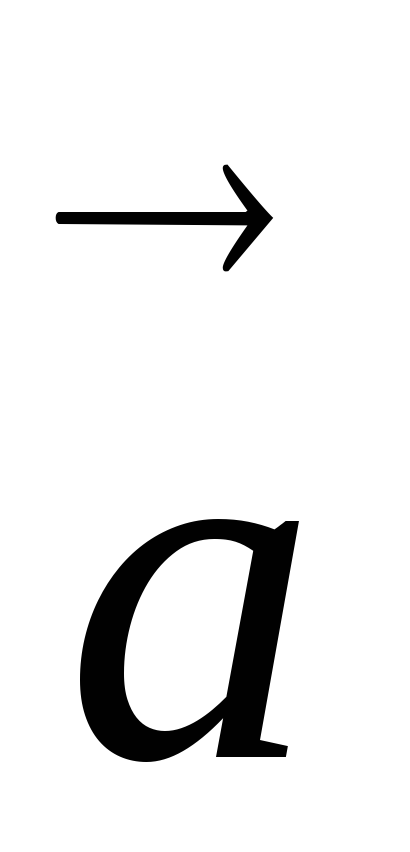 ;
;Если
 и
и неколлинеарны, то модуль векторного
произведения равен площади параллелограмма
неколлинеарны, то модуль векторного
произведения равен площади параллелограмма построенного на этих векторах, как на
сторонах.
построенного на этих векторах, как на
сторонах.
Из первых трех свойств следует, что векторное умножение суммы векторов на сумму векторов подчиняется обычным правилам перемножения многочленов. Надо только следить за тем, чтобы порядок следования множителей не менялся.
Основные орты перемножаются следующим образом:

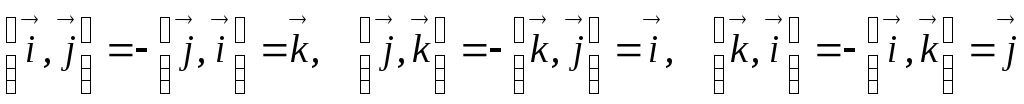 .
.
Если
![]() и
и![]() ,
тоcучетом свойств
векторного произведения векторов, можно
вывести правило вычисления координат
векторного произведения по координатам
векторов-сомножителей:
,
тоcучетом свойств
векторного произведения векторов, можно
вывести правило вычисления координат
векторного произведения по координатам
векторов-сомножителей:
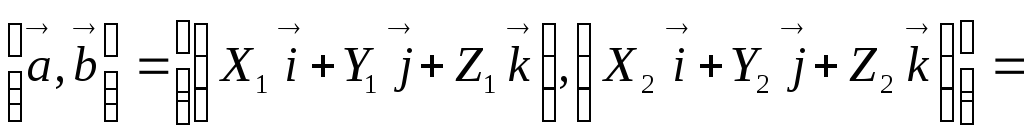
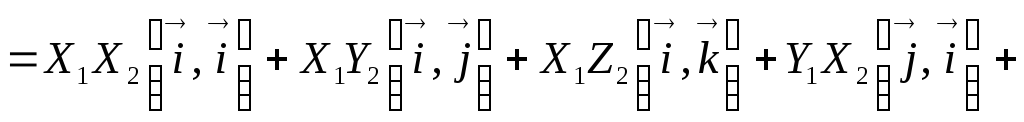
 .
.
Если принять во внимание полученные выше правила перемножения ортов, то:
|
|
(4.11) |
Более компактную форму записи выражения для вычисления координат векторного произведения двух векторов можно построить, если ввести понятие определителя матрицы.
Рассмотрим
частный случай, когда вектора
![]() и
и![]() принадлежат плоскости
принадлежат плоскости![]() ,
т.е. их можно представить как
,
т.е. их можно представить как![]() и
и![]() .
.
Если
координаты векторов записать в виде
таблицы следующим образом:
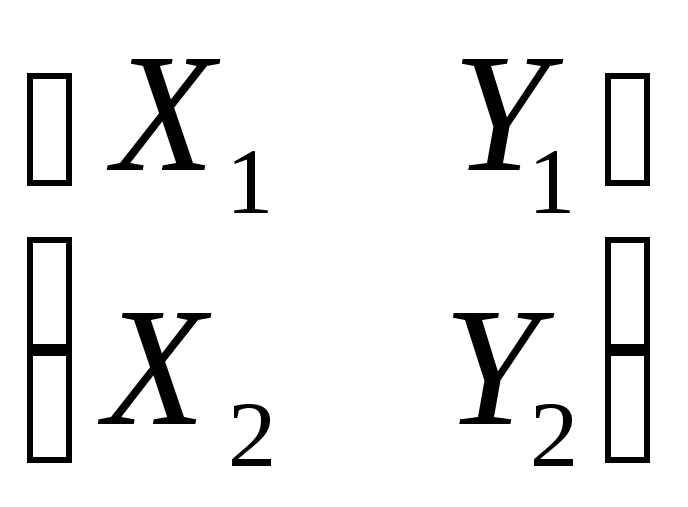 ,
то можно сказать, что из них сформирована
квадратная матрица второго порядка,
т.е. размером
,
то можно сказать, что из них сформирована
квадратная матрица второго порядка,
т.е. размером![]() ,
состоящая из двух строк и двух столбцов.
Каждой квадратной матрице ставится в
соответствие число, которое вычисляется
из элементов матрицы по определенным
правилам и называется определителем.
Определитель матрицы второго порядка
равен разности произведений элементов
главной диагонали и побочной диагонали:
,
состоящая из двух строк и двух столбцов.
Каждой квадратной матрице ставится в
соответствие число, которое вычисляется
из элементов матрицы по определенным
правилам и называется определителем.
Определитель матрицы второго порядка
равен разности произведений элементов
главной диагонали и побочной диагонали:
 .
.
В таком случае:

Абсолютная
величина определителя, таким образом,
равна площади параллелограмма,
построенного на векторах
![]() и
и![]() ,
как на сторонах.
,
как на сторонах.
Если сравнить это выражение с формулой векторного произведения (4.7), то:
|
|
(4.12) |
Это выражение представляет собой формулу для вычисления определителя матрицы третьего порядка по первой строке.
Таким образом:

Определитель матрицы третьего порядкавычисляется следующим образом:


и представляет собой алгебраическую сумму шести слагаемых.
Формулу для вычисления определителя матрицы третьего порядка легко запомнить, если воспользоваться правиломСаррюса, которое формулируется следующим образом:
Каждое слагаемое является произведением трех элементов, расположенных в разных столбцах и разных строках матрицы;
Знак “плюс” имеют произведения элементов, образующих треугольники со стороной, параллельной главной диагонали;
Знак “минус” имеют произведения элементов, принадлежащих побочной диагонали, и два произведения элементов, образующих треугольники со стороной, параллельной побочной диагонали.