Базис. Координаты вектора в базисе

Определим понятие базиса на прямой, плоскости и в пространстве.

Базисом на прямойназывается любой ненулевой векторна этой прямой. Любой другой вектор, коллинеарный данной прямой, может быть выражен через векторв виде.

Базисом на плоскостиназываются любых два линейно независимых вектораиэтой плоскости, взятые в определенном порядке. Любой третий вектор, компланарный плоскости, на которой выбран базис, может быть представлен в виде.

Базисом в трехмерном пространстве называются любые три некомпланарных вектора , взятые в определенном порядке. Такой базис обозначается. Пусть‑ произвольный вектор трехмерного пространства, в котором выбран базис. Тогда существуют числатакие, что:

(4.5)

Коэффициенты называются координатами векторав базисе, а формула (4.5) есть разложение векторапо данному базису.

Координаты вектора в заданном базисе определяются однозначно. Введение координат для векторов позволяет сводить различные соотношения между векторами к числовым соотношениям между их координатами. Координаты линейной комбинации векторов равны таким же линейным комбинациям соответствующих координат этих векторов.

Декартовы прямоугольные координаты в пространстве. Координаты точек. Координаты векторов. Деление отрезка в данном отношении

Д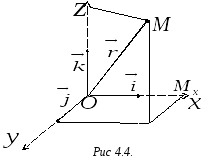екартова прямоугольная система координат в пространстве определяется заданием единицы масштаба для измерения длин и трех пересекающихся в точке взаимно перпендикулярных осей, первая из которых называется осью абсцисс, вторая – осью ординат, третья – осью аппликат; точка‑ начало координат (Рис. 4.4).

Положение координатных осей можно задать с помощью единичных векторов , направленных соответственно по осям. Векторыназываются основными или базисными ортами и определяют базисв трехмерном пространстве.

Пусть в пространстве дана точка . Проектируя ее на ось, получим точку. Первой координатойилиабсциссой точки называется длина вектора, взятая со знаком плюс, еслинаправлен в ту же сторону, что и вектор, и со знаком минус ‑ если в противоположную. Аналогично проектируя точкуна осии, определим ееординату иаппликату .Тройка чиселвзаимно однозначно соответствует точке.

Система координат называется правой, если вращение от осик осив ближайшую сторону видно с положительного направления осисовершающимися против часовой стрелки, илевой, если вращение от осик осив ближайшую сторону видно совершающимися по часовой стрелке.

Вектор , направленный из начала координат в точкуназываетсярадиус-вектором точки , т.е.:

(4.6)

Если даны координаты точек и, то координаты вектораполучаются вычитанием из координат его концакоординат начала:или.

Следовательно, по формуле (4.5):

или

(4.7)

При сложении (вычитании) векторов их координаты складываются (вычитаются), при умножении вектора на число все его координаты умножаются на это число.

Длина вектора равна квадратному корню из суммы квадратов его координат.

.

(4.8)

Длина вектора ,заданного координатами своих концов, т.е. расстояние между точками и вычисляется по формуле:

.

(4.9)

Если иколлинеарны, то они отличаются друг от друга скалярным множителем. Следовательно, у коллинеарных векторов координаты пропорциональны:

.

(4.10)

Пусть точка делит отрезок между точкамиив отношении, тогда радиус-вектор точкивыражается через радиусы-векторыиего концов по формуле:.

Отсюда получаются координатные формулы:

.

В частности, если точка делит отрезокпополам, тои, т.е..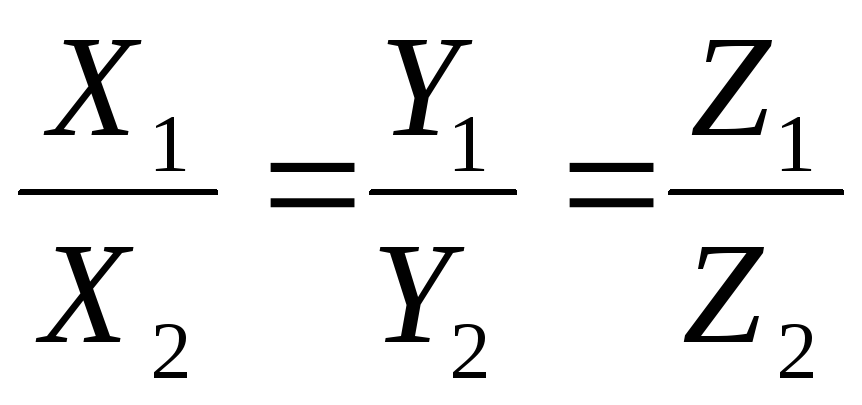