
- •Академия управления при Президенте Республики Беларусь
- •Содержание
- •Тема 4. Функции 9
- •Тема 5. Дифференциальное исчисление функций одной переменной 34
- •Тема 6. Исследование функций 45
- •Тема 7. Пространство 66
- •Тема 8. Неопределенные интегралы 100
- •Тема 9. Определенные интегралы 114
- •Тема 10. Понятие кратного интеграла 132
- •Тема 11. Ряды 140
- •Тема 12. Дифференциальные уравнения 171
- •Тема 4. Функции Лекция 15. Функции
- •Основные понятия
- •Понятие числовой последовательности
- •Сходящиеся последовательности
- •Бесконечный предел
- •Замечательные пределы
- •Принцип сходимости
- •Предел функции. Теорема Гейне
- •Односторонние пределы
- •Пределы на бесконечности
- •Бесконечные пределы
- •Непрерывность функции
- •Непрерывность композиции
- •Точки разрыва
- •Контрольные вопросы к теме №4
- •Тема 5. Дифференциальное исчисление функций одной переменной Лекция 16. Дифференциальное исчисление функций одной переменной
- •Определение и смысл производной
- •Построение касательной к графику функции
- •Экономический смысл производной
- •Эластичность функции
- •Дифференцируемость функции
- •Правила дифференцирования
- •Производная сложной функции
- •Производная обратной функции
- •Дифференциал
- •Приближенные вычисления
- •Свойства дифференцируемых функций
- •Правила Лопиталя
- •Монотонность функции
- •Локальный экстремум
- •Исследование стационарных точек
- •Глобальный экстремум
- •Выпуклость и перегибы графика функции
- •Исследование функции и построение графика
- •Интерполяция и аппроксимация функций
- •Интерполяционный полином Лагранжа
- •Формула Тейлора
- •Основные разложения
- •Понятие об эмпирических формулах
- •Контрольные вопросы к теме №6
- •Тема 7. Пространство Лекция 18. Пространство
- •Точки, расстояние. Множества в
- •Последовательности в. Сходимость
- •Функции в. Предел. Теорема Гейне
- •Непрерывность функции в
- •Непрерывность на множестве
- •Теоремы о непрерывности
- •Дифференцируемость функций в. Частные производные
- •Дифференциал функции нескольких переменных
- •Необходимые условия дифференцируемости. Достаточные условия
- •Дифференцирование функции, заданной неявно и композиции функций
- •Полные дифференциалы и частные производные высших порядков. Признак полного дифференциала
- •Формула Тейлора
- •Локальный экстремум функции нескольких переменных. Необходимое и достаточное условия. Исследование стационарных точек
- •Условный экстремум функций нескольких переменных. Глобальный экстремум
- •Метод наименьших квадратов
- •Контрольные вопросы к теме №7
- •Свойства неопределенного интеграла
- •Замена переменных
- •Интегрирование по частям
- •Интегрирование рациональных функций. Метод рационализации
- •Вычисление
- •Вычисление
- •Вычисление
- •Вычисление
- •Контрольные вопросы к теме №8
- •Тема 9. Определенные интегралы Лекция 20. Определенные интегралы
- •Интегральные суммы
- •Необходимое и достаточное условие интегрируемости
- •Равномерно непрерывные функции
- •Интегрируемость непрерывных, разрывных и монотонных функций
- •Основные свойства определенного интеграла
- •Оценки интегралов. Формулы среднего значения
- •Основные правила интегрирования
- •Приложения определенного интеграла Площадь плоской фигуры
- •. Объемы тел вращения
- •Несобственные интегралы
- •Интегрирование неограниченных функций
- •Интегрирование по бесконечному промежутку
- •Приближенное вычисление определенных интегралов
- •Формула прямоугольников
- •Формула трапеций
- •Контрольные вопросы к теме №9
- •Тема 10. Понятие кратного интеграла Лекция 21. Понятие кратного интеграла
- •Интегрирование функций многих переменных
- •Свойствакратного интеграла
- •Контрольные вопросы к теме №10
- •Тема 11. Ряды Лекция 22. Ряды
- •Основные понятия
- •Положительные ряды
- •Знакочередующиеся ряды
- •Абсолютная сходимость
- •Функциональные ряды
- •Степенной ряд
- •Ряды Фурье
- •Ряды Фурье четных и нечетных функций
- •Понятие о рядах Фурье непериодических функций
- •Контрольные вопросы к теме №11
- •Тема 12. Дифференциальные уравнения Лекция 23. Дифференциальные уравнения
- •Основные понятия
- •Дифференциальные уравнения первого порядка
- •Дифференциальные уравнения семейства кривых
- •Геометрическое истолкование дифференциального уравнения
- •Задача Коши
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения
- •Линейные дифференциальные уравнения
- •Метод Эйлера приближенного решения дифференциальных уравнений
- •Дифференциальные уравнения второго порядка
- •Задача Коши
- •Интегрируемые типы дифференциальных уравнений второго порядка
- •Случаи понижения порядка
- •Общие свойства решений линейных однородных дифференциальных уравнений второго порядка
- •Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные неоднородные уравнения второго порядка с постоянными коэффициентами
- •Линейные дифференциальные уравнения-го порядка
- •Контрольные вопросы к теме №12
- •Вопросы к экзамену
- •Литература
- •Высшая математика
- •220007, Г. Минск, ул. Московская, 17.
Интегрирование рациональных функций. Метод рационализации
Из
курса линейной алгебры известно, что
рациональной дробью называется выражение
вида
 ,
где
,
где![]() и
и![]() – многочлены степени
– многочлены степени![]() и
и![]() ,
соответственно. Рациональная дробь
называется правильной при
,
соответственно. Рациональная дробь
называется правильной при![]() .
В противном случае, когда
.
В противном случае, когда![]() ,
рациональная дробь называется
неправильной. Деление числителя на
знаменатель позволяет от неправильной
дроби перейти к правильной.
,
рациональная дробь называется
неправильной. Деление числителя на
знаменатель позволяет от неправильной
дроби перейти к правильной.
При
интегрировании правильной рациональной
дроби производится разложение этой
дроби на простейшие, для чего предварительно
разлагается на элементарные множители
многочлен
![]() .
Коэффициенты разложения определяются
методом неопределенных множителей.
Почленное интегрирование результатов
разложения сводится к вычислению
интегралов вида:
.
Коэффициенты разложения определяются
методом неопределенных множителей.
Почленное интегрирование результатов
разложения сводится к вычислению
интегралов вида: и
и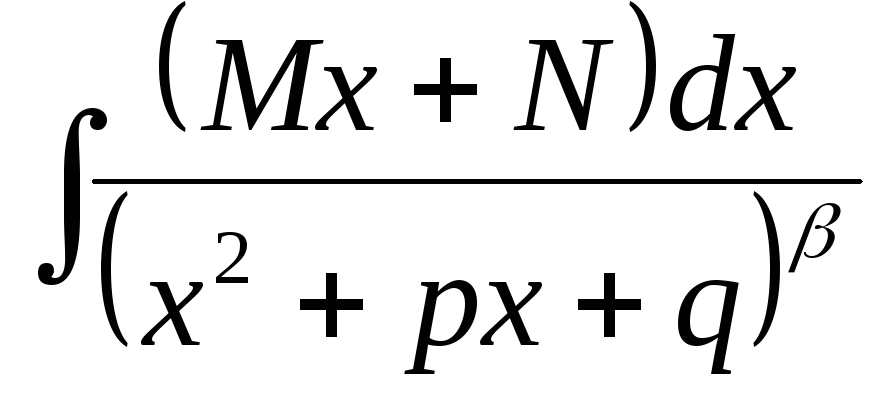 .
.
Интегралы
вида
 вычисляются следующим образом:
вычисляются следующим образом:
 ;
; ;
;
Для
вычисления интегралов вида
 применяются метод замены переменных и
метод интегрирования по частям:
применяются метод замены переменных и
метод интегрирования по частям:
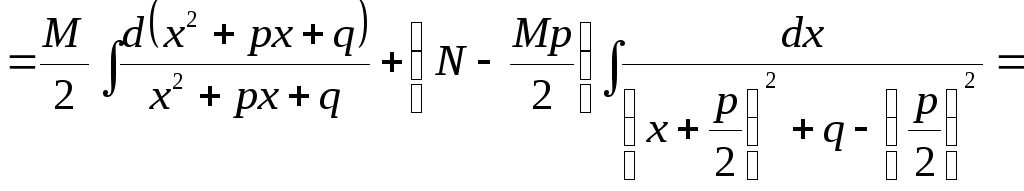
 ;
;
Обозначим
 через
через![]() ,
тогда
,
тогда .
Введем новую переменную
.
Введем новую переменную ,
тогда
,
тогда![]() ,
,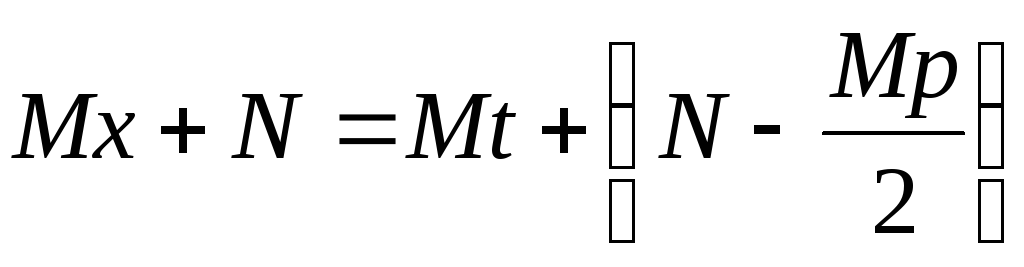 .
.

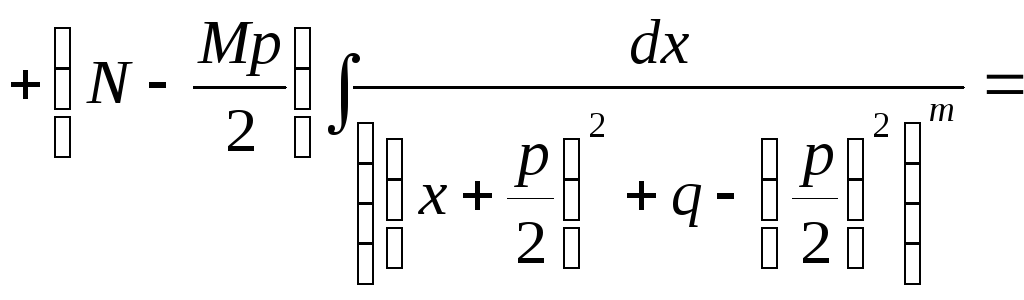
 ;
;
 .
.

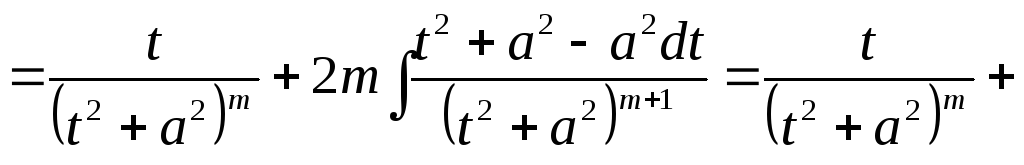
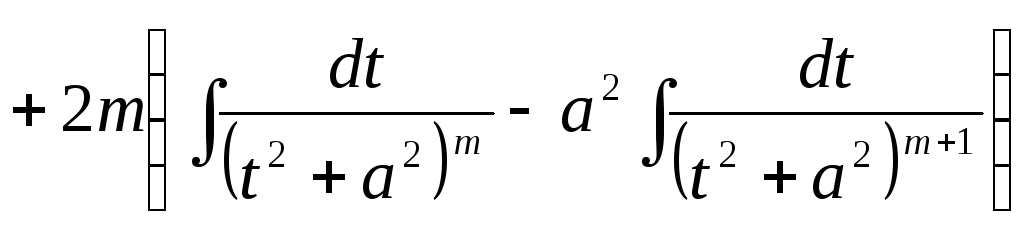 .
.
Если
ввести обозначение
 ,
то полученное выражение можно переписать
в следующем виде:
,
то полученное выражение можно переписать
в следующем виде:

Таким
образом, происходит понижение порядка
вычисляемого интеграла, и вычисление
интеграла
![]() сводится к вычислению интеграла
сводится к вычислению интеграла![]() .
.
Зная
с точностью до константы интеграл
 можно вычислить
можно вычислить![]() :
:
 .
.
Используя
полученный результат, можно вычислить
![]() :
:

Таким
образом, можно вычислить интеграл
![]() для любого натурального
для любого натурального![]() .
.
Вычисление
Во многих случаях интегрирование иррациональной функции удается выполнить, применив замену переменной интегрирования, преобразующую подынтегральную функцию в рациональную.
Если
![]() рациональная
функция своих аргументов, а
рациональная
функция своих аргументов, а![]() целые положительные числа, то интеграл:
целые положительные числа, то интеграл:
![]()
приводится
к интегралу от рациональной функции
при помощи подстановки
![]() ,
где
,
где![]() наибольшее
общее кратное показателей корней
наибольшее
общее кратное показателей корней![]() .
.
Сходная подстановка рационализирует подынтегральную функцию и в более общем случае интегрирования выражений типа:
 .
.
В
этом случае также применяется подстановка
 ,
где, как и в рассмотренном выше случае,
,
где, как и в рассмотренном выше случае,![]() наибольшее
общее кратное показателей корней
наибольшее
общее кратное показателей корней![]() .
.
Вычисление
Интеграл
![]() сводится к интегралу от рациональной
функции с помощью одной из следующих
подстановок:
сводится к интегралу от рациональной
функции с помощью одной из следующих
подстановок:
Если
 ,
то
,
то ;
;Если
 ,
то
,
то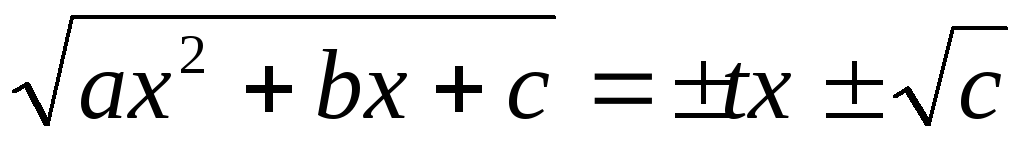 ;
;Если
 ,
,
то
![]() .
.
Здесь
![]() - новая переменная.
- новая переменная.
Интеграл
![]() находится подстановкой
находится подстановкой![]() .
.
Интеграл
![]() находится подстановкой
находится подстановкой![]() .
.
Интеграл
![]() находится подстановкой
находится подстановкой .
.
Пример:Вычислить .
.
Применим
подстановку Эйлера
![]() .
Возводя это равенство почленно в квадрат,
получим
.
Возводя это равенство почленно в квадрат,
получим![]() .
Дифференцируя обе части полученного
выражения, получим
.
Дифференцируя обе части полученного
выражения, получим![]() .
Отсюда
.
Отсюда![]() ,
или
,
или .
Таким образом,
.
Таким образом, .
Поскольку
.
Поскольку![]() ,
то
,
то![]() .
Следовательно,
.
Следовательно, .
.
Вычисление
Интеграл
![]() ,
где
,
где![]() - рациональная функция, всегда сводится
к интегралу от рациональной функции
при помощи универсальной подстановки
- рациональная функция, всегда сводится
к интегралу от рациональной функции
при помощи универсальной подстановки .
При этом:
.
При этом:
 .
.
При
вычислении таких интегралов можно
использовать также и специальные
подстановки, а именно: в случае, когда
![]() ,
можно использовать подстановку
,
можно использовать подстановку![]() .
.
В
случае неопределенного интеграла вида
![]() это соответствует нечетному значению
это соответствует нечетному значению![]() .
.
Если
![]() ,
можно использовать подстановку
,
можно использовать подстановку![]() .
.
Если
![]() ,
то можно использовать подстановку
,
то можно использовать подстановку![]() .
.
Вычисление
Интеграл
от дифференциального бинома, т.е. интеграл
![]() ,
где
,
где![]() рациональные числа,
рациональные числа,![]() и
и![]() постоянные, отличные от нуля, сводится
к интегралу от рациональной функции в
трех случаях:
постоянные, отличные от нуля, сводится
к интегралу от рациональной функции в
трех случаях:
когда
 целое число, – разложением на слагаемые
по формуле бинома Ньютона;
целое число, – разложением на слагаемые
по формуле бинома Ньютона;когда
 целое число, – подстановкой
целое число, – подстановкой ,
где
,
где знаменатель дроби
знаменатель дроби ;
;когда
 целое число, – подстановкой
целое число, – подстановкой .
.
Как мы видим, не существует сколько-нибудь общих приемов нахождения неопределенных интегралов от любой элементарной функции. Более того, доказано, что многие, порой очень простые на первый взгляд, интегралы не выражаются через элементарные функции, или, как говорят, не берутся. Например, к таким интегралам относятся:
 .
.
В различных справочниках приводятся таблицы, в которых содержится большое количество неопределенных интегралов, как выражающихся, так и не выражающихся через элементарные функции.


