Приклад 7.

Обчислити

Розв´язання.

Тут P(n)=3n²-4n+5, Q(n)=n³-8n, які при мають границею нескінченність,m=2, k=3, тому ділимо кожен член многочленів на n³ і з´ясовуємо до чого прагне кожен з отриманих членів.

Зауваження. Проміжні дії позначають в квадратних дужках.

Приклад 8.

Обчислити:

1) 2)3)

Розв´язання.

1) ;

2) ;

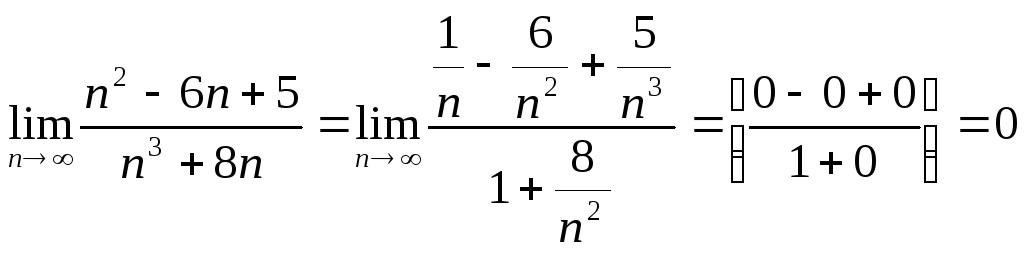3) .

Зауважимо, що тут не відбувається ділення на нуль, оскільки знаменник лише прагне до нуля, але йому не дорівнює, а при діленні на дуже маленьке число отримується дуже велике, тому отримали нескінченність.

Проаналізуємо отримані відповіді приклада 8. В прикладі 8.1. степені чисельника і знаменника однакові і в результаті отримали відношення коефіцієнтів при старших степенях ( в чисельнику – число 5, в знаменнику – (-1)). В прикладі 8.2. степінь чисельника менше за степінь знаменника, це означає, що знаменник прямує до нескінченності швидше ніж чисельник, а отже їх відношення буде дорівнювати нулю. В прикладі 8.3., навпаки, степінь чисельника більше за степінь знаменника, це означає, що чисельник прямує до нескінченності швидше ніж знаменник, а отже їх відношення дорівнює нескінченності. Маємо ще таке правило.

Правило. Для того, щоб обчислити границю числової послідовності при , яка задається як відношення двох многочленіводнієї змінної п степенів т і к відповідно, і кожен з яких має границю, що дорівнює нескінченності, необхідно порівняти ці степені, якщо:

1. т=к, то границя дорівнює відношенню коефіцієнтів при старших степенях заданих многочленів;

2. m<k, то границя дорівнює нулю;

3. m>k, то границя дорівнює нескінченності.

Правило. Для того, щоб обчислити границю числової послідовності при , яка задається як многочлен, який містить ірраціональні вирази, необхідно помножити його та поділити на вираз, спряжений до заданого.

Приклад 9.

Обчислити

Розв´язання.

Тема 2. Границя функції неперервного аргументу.

1. Означення границі функції за Гейне і за Коші.

2. Властивості функцій, які мають границю в точці.

3. Арифметичні властивості границь функції.

4. Границя функції на нескінченності.

5. Перша важлива границя.

6. Друга важлива границя.

7. Порівняння нескінченно малих функцій. Еквівалентні нескінченно малі функції.

1. Означення границі функції за Гейне і за Коші.

Розглянемо функціюy=f(x), де аргумент змінюється неперервно (набуває всіх значень з певного проміжку (a;b), крім, можливо, однієї внутрішньої точки даного проміжку)

Наприклад. Розглянемо функцію f(х) =х²+1 , коли х наближається

до числа 2.

Як видно з рисунка 2, коли х наближається до числа 2 зліва або справа, то значення функції наближається до числа 5, тобто ці значення мало відрізняються від числа 5. Отже, значення функції f(х)=х²+1 при х→2 має границею число 5.

Записують це так:

З геометричної точки зору попередній приклад

можна пояснити так. Якщо на осі Оу побудувати відрізок завдожки 2ε з центром в точці 5 (його називають ε-околом точки), то всі значення функції, які містяться в ньому будуть

задовольняти нерівність 5-ε<f(x)<5+ε, або -ε<f(x)-5<ε,

або за властивостями модуля: |f(x)-5|<ε. Проте поведінка функції залежить від значень, яких набуває аргумент х. З´ясуємо геометрично, для яких х виконується отримана нерівність. Для цього опустимо з кінців відрізка [5-ε; 5+ε] перпендикуляри на вісь Ох. Позначимо отриманий відрізок на осі Ох через [2-δ; 2+δ], отже в нього потраплять всі значення аргумента, при яких значення функції потраплять в ε-окіл точки 5. Алгебраїчно це означає, що при |x-2|<δ | f(x)-5|<ε.

Можна зробити такі висновки. Якщо число А є границею функції y=f(x) при х→х₀, то значення функції як завгодно близько наближаються до числа А, коли значення аргументу х як завгодно близько наближаються до числа х_0.

Наприклад. Розглянемо функцію , колих

наближається до числа 3. На відміну від попереднього прикладу, функція в точці 3 є невизначеною, тому скористаємось її графіком (рис.3). Як видно з нього, при х→3 функція має границею число 6.

Отже, .

Значення δ>0 для будь-якого наперед заданого числа ε>0 можна знайти алгебраїчним способом, розв´язавши відповідну нерівність |f(x)-А|<ε відносно |x-x₀|. Так для попереднього прикладу задамо ε>0 і знайдемо відповідне значення δ>0, таке щоб для всіх х≠3 і таких, що |x-3|<δ виконувалось |f(x)-6|<ε. Матимемо: . Розв´яжемо цю нерівність відносно |x-3|. Враховуючи, що х≠3, маємо:

. Отже в даному випадку за δ можна взяти δ=ε.

Існують такі два означення функції в точці: за Гейне (через послідовності) та за Коші (через ε-δ-окіл).

Означення 2.1. (означення границі функції в точці за Гейне). Нехай функція визначена в околі Х точких₀ крім можливо самої точки х₀. Число А називається границею функції в точці х₀, якщо для будь-якої послідовності числові послідовностімають своєю границею числоА. Позначення:.

Означення 2.2. (означення границі функції в точці за Коші). Нехай функція визначена в околі Х точких_0, крім, можливо, самої точки х₀. Число А називається границею функції в точці х₀, якщо для будь-якого ε>0 існує δ(ε) >0, що для всіх х із околу Х, таких, що , виконується нерівність .

Означення за Гейне і за Коші – еквівалентні.

У наведених вище означеннях границі вважалося, що х прямує до х₀ довільним способом: залишаючись меншим від х₀ (зліва від х₀), більшим х₀ (справа від х₀) чи коливаючись навколо х₀ , тобто, набуваючи значень то менших, то більших відх₀ (то зліва то справа від х₀), як амплітуда затухаючих коливань маятника. У зв’язку з цим вводяться поняття односторонніх границь.

Означення 2.3. Нехай функція визначена в деякому околі точких₀. Число А називається границею функції зліва (або лівосторонньою) в точці х₀, якщо для будь-якого ε>0 існує δ(ε) >0 таке, що при виконується нерівність .

Позначають

Означення 2.4. Нехай функція визначена в деякому околі точких₀. Число В називається границею функції справа (або правосторонньою) в точці х₀, якщо для будь-якого ε>0 існує δ(ε)>0 таке, що при виконується нерівність .Позначають .