1. Задачі, які приводять до поняття похідної.

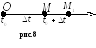а) Задача про швидкість руху. Нехай матеріальна точка рухається нерівномірно вздовж деякої прямої (рис.8) і за час t проходить відстань S, що дорівнює відрізку ОМ. Відстань рухомої точки є деякою функцією часу: .Треба знайти величину миттєвої швидкості руху точки М. Нехай з моменту t пройшов деякий час ∆t. За час ∆ t рухома точка перейде в положення М₁ і пройде шлях, який позначимо через ∆S. Отже, за час t+∆t матеріальна точка пройде шлях S+∆S=S(t+∆t), тому .

Середньою швидкістю v_c руху точки за проміжок часу ∆t називають відношення приросту шляху до приросту часу: v_c=.

Зрозуміло, що чим менший проміжок ∆t часу після t пройшов, тим точніше середня швидкість відображає швидкість руху точки у даний момент часу (миттєву швидкість). Тому миттєвою швидкістю руху точки називають границю середньої швидкості за умови, що ∆t 0:v=(1.1)

Приклад 1.

Закон руху точки виражається формулою S=t²+4t. Знайти середню швидкість руху на проміжку часу від t₀=1 с до t₁=3 с та миттєву швидкість в момент часу t₀=1 с.

Розв'язання.

Знайдемо приріст шляху ∆S за проміжок часу ∆t: =(t+∆t)²+4(t+∆t)- -( t²+4t)=t²+2t∆t+∆t²+4t+4∆t-t²-4t=2t∆t+4∆t+∆t²=(2t+4)∆t+∆t². Середня швидкість за час ∆t v_c===2t+4+∆t. Проміжок часу ∆t=3-1=2 с, тому v_c=2·1+4+2=8 м/с. Знайдемо миттєву швидкість у будь-який момент часу t: v==2t+4. Зокрема, для t₀=1 с маємо v=2·1+4=5 м/с.

б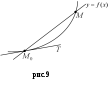)Задача про дотичну до плоскої кривої. Розглянемо криву L і на ній точки М та М₀. Пряма, яка перетинає лінією у цих двох точках називається січною. На рисунку 9 -січна. Нехай точкаМ, рухаючись по кривій, наближається до точки М₀. Тоді січна повертатиметься навколо точкиМ₀, а довжина відрізка прямуватиме до нуля. Якщо при цьому і

величина кута ММ₀Т прямує до нуля, то пряму М₀Т називають граничним положенням січної ММ₀. Пряму М₀Т, яка є граничним положенням січної ММ₀, називають дотичною до кривої L в точці М₀.

Р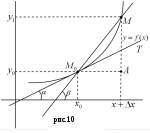озглянемо випадок, коли крива в прямокутній системі координат задана рівнянням,х є Х, - неперервна на множиніХ, має в точці М(х;у) не вертикальну дотичну. Розглянемо задачу про знаходження кутового коефіцієнта цієї дотичної. Нехай х₀ є Х. Надамо аргументу х₀ приросту х. Тоді точка М(х₀+х; f(х₀+х)). Проведемо січну М₀М, яка утворює з додатним напрямом осі Ох кут β (рис.10). З графіка видно, що

tg β=.

Якщо х0, то точка М прямує до точки М₀ вздовж кривої , а січнаММ₀, повертаючись навколо точки М, переходить в дотичну М₀Т. Кут β при цьому прямує до деякого граничного значення σ. Отже, кутовий коефіцієнт дотичної дорівнює tgσ=(1.2)

Приклад 2.

Знайти кутовий коефіцієнт дотичної до графіка функції f(x)=x²-3x+4 у точці з абсцисою х₀=1.

Розв’язання.

Знайдемо приріст функції в точці х₀=1. f(x₀)=f(1)=f(1+x)-f(1)=(1+x)²-3(1+x)+4–(1²-3+4)=1+2x+x²-3-3x+4-2=x²-x=x(x-1). Тоді кутовий коефіцієнт дотичної дорівнює tgσ= .

Пропонуємо самостійно розглянути задачі про силу струму, про густину неоднорідного стержня та інші.

Незважаючи на різний зміст розглянутих задач, всі вони приводять до знаходження границь одного і того самого виду – границі відношення приросту функції до приросту аргументу. Цю границю в математиці називають похідною функції.