Приклад 9.

Знайти похідні функції:

а) ; б).

Розв’язання.

а) Задана функція є суперпозицією 3-х функцій: v(x)=5x, u(v)=sinv, f(u)=u². Маємо: v′(x)=5, u′(v)=cosv, f′(u)=2u. А тому .

б) Аналогічно, ,.

6. Логарифмічна похідна.

Розглянемо функцію. Таку функцію називаютьстепенево-показниковою. Її похідну знаходять за допомогою логарифмічної похідної, тобто, таку функцію спочатку логарифмують, а потім знаходять похідну:

ПРИКЛАД 10.

Знайти похідну функції .

Розв’язання.

Прологарифмуємо задану функцію і знайдемо похідну:

7. Похідна функції, заданої параметрично. Диференціювання неявно заданої функції.

Нехай функція задана параметрично:х=φ(t), y=ψ(t), аtb. Тоді її похідну знаходять за формулою:

ПРИКЛАД 11.

Знайти , якщоx=4cos t, y=-6sin t.

Розв’язання.

Оскільки x'_t=-4sin t, y'_t=-6cos t, то за формулою маємо: =.

Нехай неявна функція задана рівняннямF(x,y)=0. Щоб продиференціювати неявно задану функцію, потрібно взяти похідну по х від обох частин записаної рівності, вважаючи у функцією х, і отримане рівняння розв’язати відносно у'. Похідна неявно заданої функції виражається через залежну змінну х і саму функцію у.

ПРИКЛАД 12.

Знайти похідну у', якщо 2х²+3у³-2х+5у-7=0

Розв’язання.

Продиференціюємо записану рівність, застосовуючи до другого доданку правило диференціювання складеної функції: 4х+9у² у' -2+5 у'=0 у'(9у²+5)=-4х+2 у'=

Тема 2. Диференціал.

1. Означення диференційовної функції та диференціала.

2. Властивості диференціала. Інваріантність форми диференціала.

3. Застосування диференціала.

4. Похідні та диференціали вищих порядків. Механічний зміст похідної другого порядку.

1. Означення диференційовної функції та диференціала.

Нехай задано функцію y = f(x), x є [a;b]. Виберемо точку x₀ є (a;b) і надамо їй приросту ∆x так, що x₀ + ∆x є (a;b). Обчислимо приріст функції в точці x₀:

∆f(x₀) = f(x₀ +∆x) – f (x₀).

Означення 2.1. Функція y = f(x) називається диференційовною в точці х₀, якщо її приріст у цій точці можна записати у вигляді ∆f(x₀) = А(x₀)∆х+(x₀,∆x) ∆x, де А(x₀) – число, що не залежить від ∆x і (x₀, ∆x) = 0.

Означення 2.2. Функція y = f(x) називається диференційовною на множині Х, якщо вона диференційовна у кожній точці цієї множини.

Приклад 1.

Довести, що функція диференційована в точці.

Розв’язання.

Надамо точці приростуі обчислимо відповідний приріст функції: ∆у(1)=у(1+)-у(1)=(1+)²-1²=1+2+²-1=2+². Отже, А(1)=2, α(∆х,1)=∆х і . За означенням 2.1. функціяу=х² диференційовна в точці .

Означення 2.3. Диференціалом функції y=f(x) в точці х₀ називається лінійна відносно ∆х частина приросту диференційовної в точці х₀ функції.

Позначення: d f(х₀). За означенням: d f(х₀)= А(x₀)∆х.

З’ясуємо зв'язок числа А(x₀) з функцією y = f(x). Розглянемо приріст диференційовної в точці х₀ функції: . Поділимо обидві частини рівності наі перейдемо до границі за умови, що0. Маємо:. Тоді- повний приріст диференційовної в точціх₀ функції.

Отже, для обчислення диференціала маємо формулу: df(x₀) = f ′(x₀)dx, де ∆х = dx –диференціал незалежної змінної. Використовуючи отриману формулу, можемо записати диференціали основних елементарних функцій.

Таблиця диференціалів основних елементарних функцій.

	df(x)		df(x)
с, с- стала			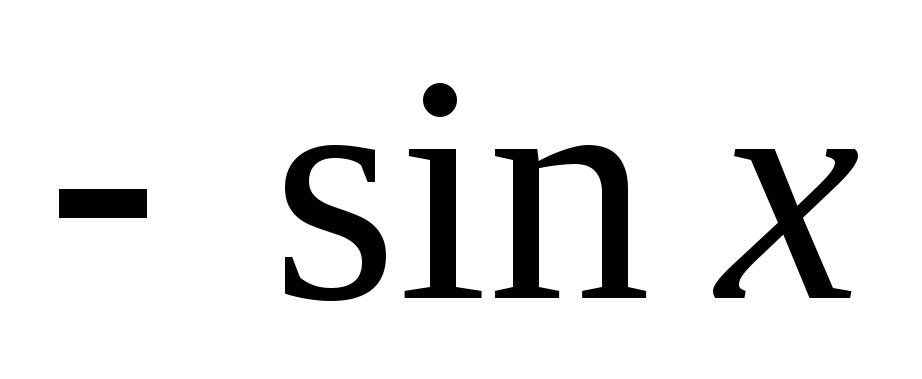dx
, k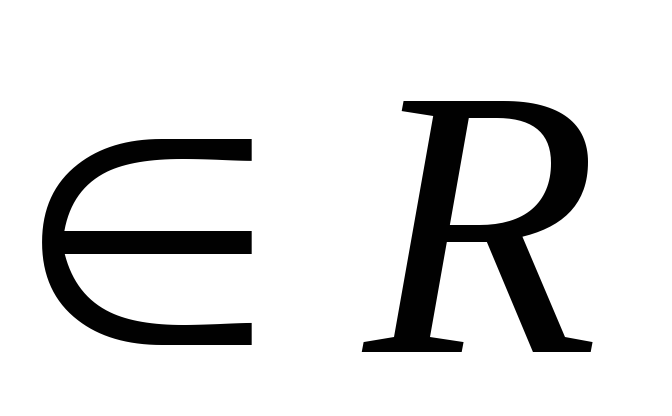	к хк-1dx		dx
	dx		dx
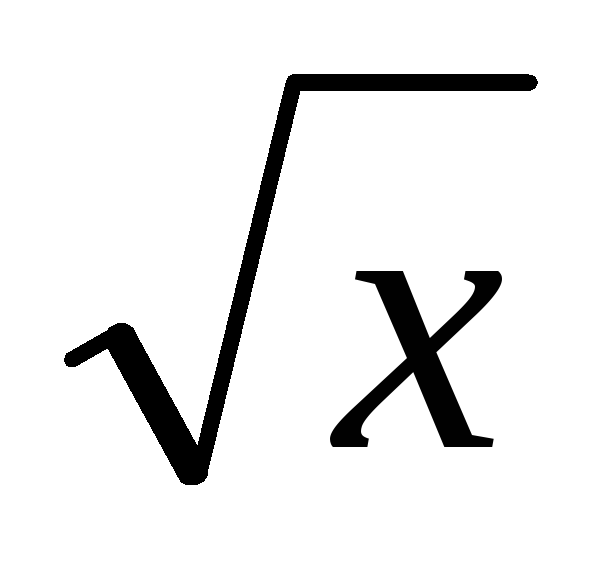
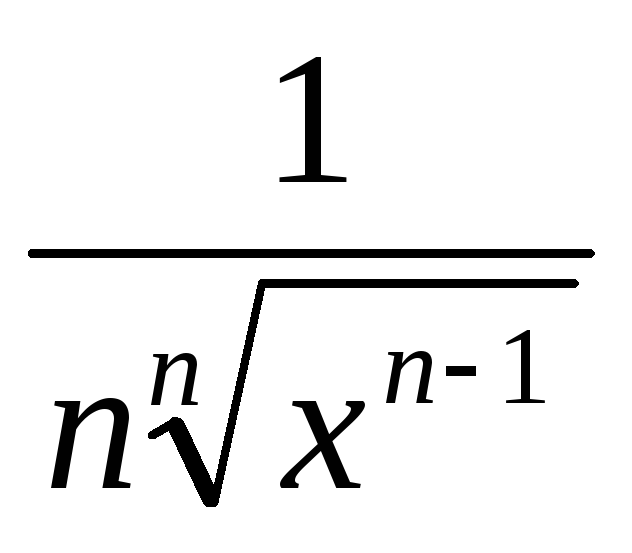	dx		dx
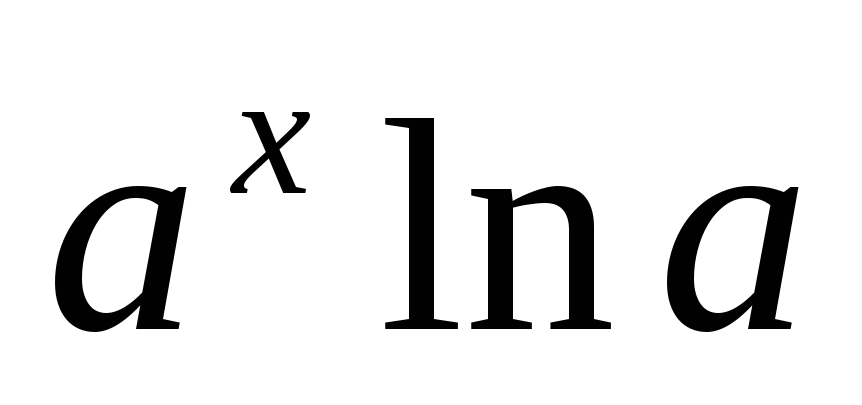
	dx		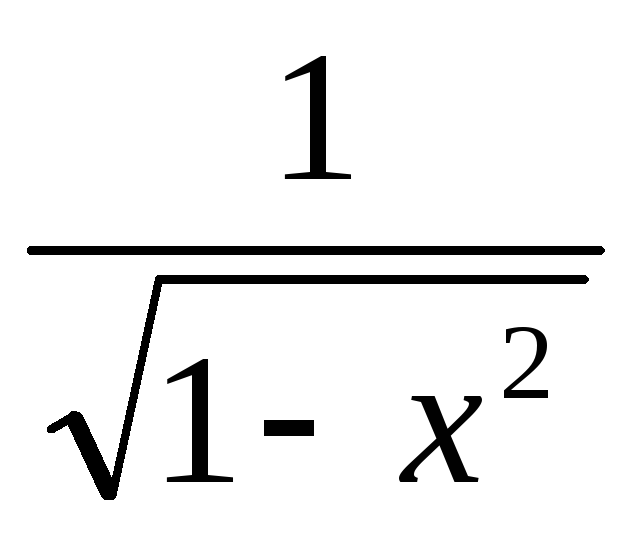dx
			- dx
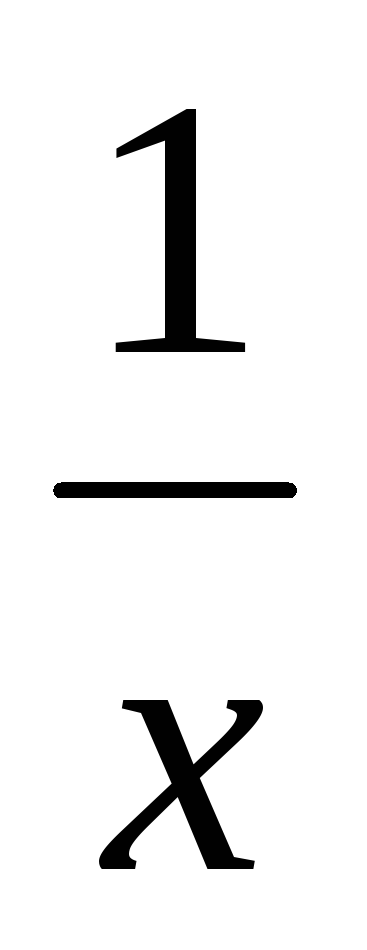
ех	ех		dx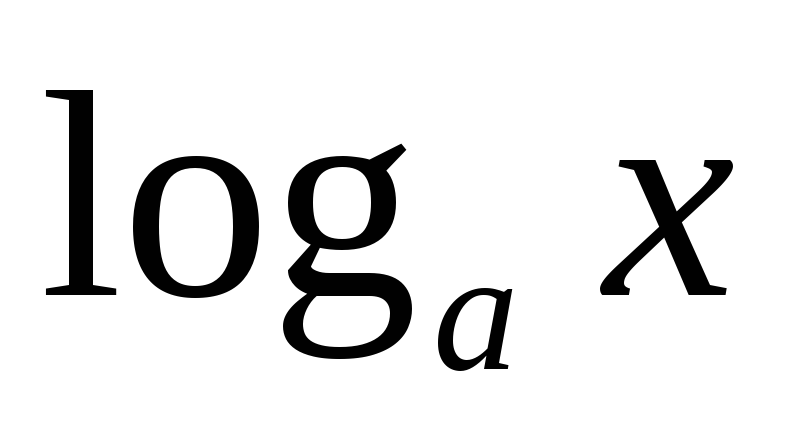
			dx
	dx

Рівність df(x₀) = f ′(x₀)dx можна переписати у вигляді . Маємо ще одне позначення похідної функції в точці.