
- •Границя числової послідовності та функції однієї змінної.
- •Тема 1. Числова послідовність та її границя.
- •1. Числова послідовність та способи її задання.
- •Основні способи задання числової послідовності:
- •2. Обмежені та монотонні числові послідовності.
- •3. Границя числової послідовності.
- •Приклад 1
- •Приклад 2
- •4. Нескінченно малі числові послідовності
- •Властивості нескінченно малих послідовностей
- •Приклад 3.
- •Приклад 4.
- •5. Нескінченно великі числові послідовності
- •6. Арифметичні властивості збіжних числових послідовностей.
- •Приклад 5.
- •Приклад 6.
- •Приклад 7.
- •Приклад 8.
- •Приклад 9.
- •Тема 2. Границя функції неперервного аргументу.
- •1. Означення границі функції за Гейне і за Коші.
- •2. Властивості функцій, які мають границю в точці
- •3. Арифметичні властивості границь функції
- •Теореми про граничні переходи.
- •Приклад 1.
- •Приклад 2.
- •4. Границя функції на нескінченності
- •Приклад 3.
- •5. Перша важлива границя
- •Приклад 4.
- •6. Друга важлива границя
- •Приклад 5.
- •7. Порівняння нескінченно малих функцій. Еквівалентні нескінченно малі функції.
- •Приклад 6.
- •Властивості еквівалентних нескінченно малих функцій.
- •Приклад 7.
- •Тема 3. Неперервність функції.
- •1. Односторонні границі функції.
- •Приклад 1.
- •2. Означення неперервності функції в точці і на проміжку.
- •3. Арифметичні дії над неперервними функціями.
- •4. Одностороння неперервність. Точки розриву та їх класифікація.
- •Класифікація точок розриву
- •Приклад 2.
- •Приклад 3.
- •Приклад 4.
- •5. Властивості функцій, неперервних на відрізку.
- •Диференціальне числення функції однієї змінної.
- •Тема 1: Похідна.
- •1. Задачі, які приводять до поняття похідної.
- •Приклад 1.
- •Приклад 2.
- •2. Означення похідної. Спосіб знаходження похідної. Геометричний та механічний зміст похідної. Рівняння дотичної та нормалі до плоскої кривої.
- •Правило знаходження похідної за означенням.
- •Приклад 4.
- •3. Диференційовні функції. Зв’язок неперервності з диференційовністю
- •Приклад 5.
- •4. Таблиця похідних основних елементарних функцій
- •5. Правила диференціювання.
- •Приклад 6.
- •Приклад 7.
- •Приклад 8.
- •Приклад 9.
- •Приклад 1.
- •2. Властивості диференціала. Інваріантність форми диференціала.
- •Приклад 2.
- •3. Застосування диференціала.
- •Приклад 3.
- •4. Похідні та диференціали вищих порядків. Механічний зміст похідної другого порядку.
- •Приклад 4.
- •Приклад 5.
- •Приклад 6.
- •Тема 3. Теореми про середнє. Правила Лопіталя.
- •1. Теорема Ферма.
- •2. Теорема Ролля.
- •Приклад 1.
- •3. Теорема Лагранжа.
- •Приклад 2.
- •Приклад 3.
- •Приклад 1.
- •2. Локальний екстремум функції.
- •З’ясуємо умови існування локального екстремуму.
- •Приклад 2.
- •Приклад 3.
- •Приклад 4.
- •3. Найбільше і найменше значення функції.
- •Приклад 5.
- •Приклад 6.
- •4. Опуклість і вгнутість кривих. Точки перегину.
- •Приклад 7.
- •5. Асимптоти кривої.
- •Приклад 8.
- •6. Схема дослідження функції та побудова її графіка.
- •Приклад 9.
- •Інтегральне числення функції однієї змінної
- •Тема 1. Невизначений інтеграл
- •Поняття первісної та невизначеного інтегралу
- •Приклад 1.
- •Властивості невизначеного інтеграла (ні).
- •4. Основні методи інтегрування
- •4.1. Метод безпосереднього інтегрування (мбі)
- •Приклад 2.
- •4.2. Метод заміни змінної (мзз)
- •Приклад 3.
- •4.3. Метод інтегрування частинами (міч)
- •Приклад 4.
- •Цей метод використовують під час обчислення інтегралів виду
- •Приклад 5.
- •Загальне правило інтегрування раціональних дробів.
- •Приклад 6.
- •Він зводиться до інтеграла від раціональної функції підстановкою . Приклад 7.
- •Обчислити
- •Обчислити
- •Обчислити
- •Обчислити
- •4.6. Біноміальний диференціал
- •Приклад 8.
- •4.7. Інтегрування тригонометричних функцій
- •Приклад 10.
- •Поняття визначеного інтеграла.
- •2. Властивості визначеного інтеграла.
- •4. Теорема Ньютона-Лейбніца (н-л)
- •Приклад 1.
- •5. Методи знаходження ві.
- •5.1. Метод безпосереднього інтегрування
- •Приклад 2.
- •5. 2. Метод заміни змінної
- •Приклад 3.
- •Приклад 4.
- •5.3. Метод інтегрування частинами
- •Приклад 5.
- •Приклад 6.
- •Формули зведення. Формула інтегрування частинами
- •Приклад 7.
- •Приклад 2.
- •Приклад 3.
- •Площа криволінійного сектора
- •Приклад 4.
- •3. Обчислення довжини дуги
- •Приклад 5.
- •Приклад 6.
- •Обчислення тиску рідини на вертикальну пластину
- •9. Невласні інтеграли із нескінченним проміжком інтегрування
- •Приклад 10.
- •Приклад 11.
- •Обчислення невласних інтегралів від розривних (необмежених) функцій
- •Приклад 12.
4.6. Біноміальний диференціал
Означення
1.3.. Вираз
виду
![]() ,
де
,
де![]() і
і![]() — сталі показники,
— сталі показники,![]() — раціональні числа, називаєтьсябіноміальним
диференціалом.
— раціональні числа, називаєтьсябіноміальним
диференціалом.
Цей диференціал введенням нової змінної можна перетворити на диференціал такого самого виду, але з цілими показниками.
●Справді,
беручи
![]() дістаємо
дістаємо
![]()
Узявши
![]() так, щоб
так, щоб![]() і
і![]() були цілими, знайдемо біноміальний
диференціал з цілими показниками.
були цілими, знайдемо біноміальний
диференціал з цілими показниками.
Далі
з тотожності
![]() випливає, що біноміальний диференціал
може бути перетворений на диференціалтипу
випливає, що біноміальний диференціал
може бути перетворений на диференціалтипу
![]() ,
,
але
до нього замість
![]() входить –n,
а отже, в
одному з двох диференціалів показник
буде додатним. Таким чином, не порушуючи
загальності, можемо вважати, що
входить –n,
а отже, в
одному з двох диференціалів показник
буде додатним. Таким чином, не порушуючи
загальності, можемо вважати, що
![]() і
і![]() — цілі числа і
— цілі числа і![]() —
додатне.
—
додатне.
Отже існує три випадки інтегрованості у скінченному вигляді біноміальних диференціалів
І.
![]() — ціле число. Тоді біноміальний
диференціал — є звичайною раціональною
функцію.
— ціле число. Тоді біноміальний
диференціал — є звичайною раціональною
функцію.
ІІ.
![]() —не
ціле число,
але виконується умова
—не
ціле число,
але виконується умова
![]()
Тоді біноміальний диференціал обчислюється виконуючи заміну
![]()
В результаті підстановки якої отримаємо також раціональну функцію.
ПРИКЛАД 7.

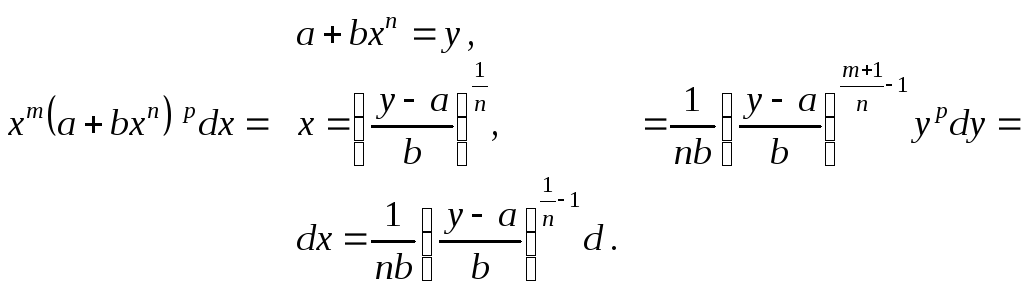

ІІІ.
![]() —не
ціле число, але
—не
ціле число, але
![]()
Тоді,
застосувавши заміну
![]() до виразу
до виразу
![]() дістанемо:
дістанемо:

![]()

Ці випадки інтегровності були відомі ще І. Ньютонові. Але лише П. Л. Чебишов встановив, що інших випадків інтегровності у скінченому вигляді для біноміальних диференціалів не існує. Тобто, якщо ви маєте біноміальний диференціал даного виду і перевірили, що всі три випадки не виконуються, то можете стверджувати, що такий інтеграл обчислити не можливо (існують наближені методи, але вони не дають точних результатів)
Приклад 8.
Обчислити
![]()
Розв’язання.

У разі, якщо
![]() ,
аp, q— цілі числа, для обчислення інтегралів
від біноміального диференціала можна
застосувати формули зведення.
,
аp, q— цілі числа, для обчислення інтегралів
від біноміального диференціала можна
застосувати формули зведення.
Інтеграл
![]() можна звести до інтегралів
можна звести до інтегралів![]() або
або![]() :
:

4.7. Інтегрування тригонометричних функцій
Розглянемо
![]() ,,
деR
— раціональна функція відносно sinx,
cosx, тобто
над sinx, cosx
виконуються лише арифметичні дії та
піднесення до цілого степеня, наприклад:
,,
деR
— раціональна функція відносно sinx,
cosx, тобто
над sinx, cosx
виконуються лише арифметичні дії та
піднесення до цілого степеня, наприклад:
![]() .
.
Існують
такі підстановки, що за їх допомогою
інтеграл
![]() завжди може бути зведений до інтеграла
від раціональної функції
завжди може бути зведений до інтеграла
від раціональної функції![]() ,,
загальна схема інтегрування якої
розроблена.
,,
загальна схема інтегрування якої
розроблена.
І .
Універсальна тригонометрична підстановка
.
Універсальна тригонометрична підстановка![]() .
.

![]() .
.
.
ПРИКЛАД 9.
Обчислити
![]()
Розв’язання.

![]() .
.
Зауваження. На практиці універсальну тригонометричну підстановку використовують, якщо sinx, cosx входять у невисокому степені (інакше розрахунки будуть дуже складні).
ІІ. Підінтегральна функція — непарна відносно sin x, тоді роблять підстановку cosx = t.
Приклад 10.
Обчислити
![]()
![]()
Розв’язання.
![]()

![]() .
.
ІІІ. Підінтегральна функція — непарна відносно cos x раціоналізується за допомогою підстановки sin x = t.
ПРИКЛАД 11.
Обчислити
![]()
Розв’язання.
![]()

![]() .
.
IV.
Підінтегральна функція
![]() — парна поsin x,
cos x сукупно,
тобто
— парна поsin x,
cos x сукупно,
тобто
![]() ..
..
В
цьому випадку використовують підстановку
![]() або
або![]() ..
..
ПРИКЛАД 12.
Обчислити
![]()
Розв’язання.
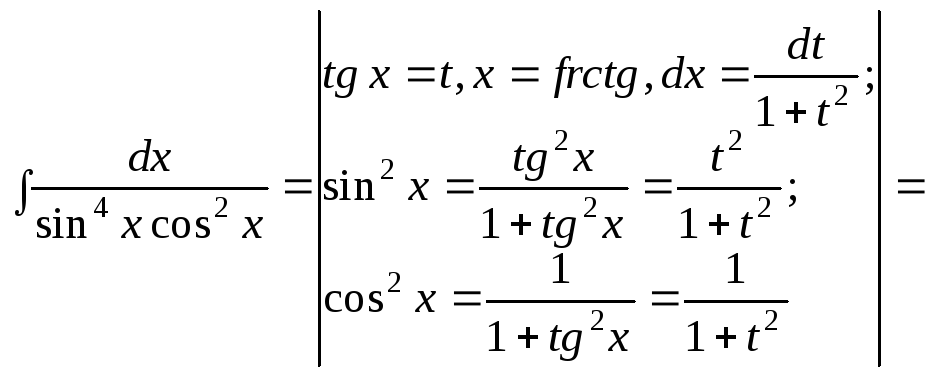
![]()
![]() .
.
V.
Підінтегральна функція
![]() раціоналізується підстановкою
раціоналізується підстановкою![]() .
.
ПРИКЛАД 13.
Обчислити
![]()
![]()
Розв’язання.

![]()
Зауваження.
В інтегралах
![]() рекомендується скористатись формулами
пониження степеня:
рекомендується скористатись формулами
пониження степеня:
![]() .
.
ПРИКЛАД 14.
Обчислити
![]()
Розв’язання.
![]() .
.
Зауваження. При інтегруванні інтегралів типу:
![]() ,
,
![]() ,
,![]()
![]() ,, треба скористатися формулами:
,, треба скористатися формулами:![]() ,
,
![]() ,
,
![]()
ПРИКЛАД 15.
Обчислити
![]()
Розв’язання.
![]() .
.
Тема 2. Визначений інтеграл та його обчислення.
Підсумовування нескінченно малих
Поняття визначеного інтеграла
Властивості визначеного інтеграла
4. Теорема Ньютона-Лейбніца (Н-Л)
5. Методи знаходження ВІ.
5.1. Метод безпосереднього інтегрування
Метод заміни змінної
Метод інтегрування частинами
5.4. Обчислення визначених інтегралів за допомогою властивостей підінтегральних функцій
1. Підсумовування нескінченно малих
Нехай задано неперервну функцію на відрізку [a; b] і F(x) —будь-яка її первісна. Розіб’ємо відрізок [a; b] на n частин і утворимо різницю значень первісної на його кінцях: F(b) – F(a) (1)
Різниця (1) дорівнює сумі таких самих різниць, складених для відрізків, на які розбито даний:
![]() (2)
(2)
За теоремою Лагранжа про скінченний приріст маємо:
F(хі) – F(хі – 1) = (хі – хі – 1)F(i – 1),
де i [хі; хі–1] (рис. 16).
П означившихі
– хі–1 =
хі–1
і врахувавши, що
означившихі
– хі–1 =
хі–1
і врахувавши, що
F(i–1) = f(i–1),
рівність (2) подамо так:
F(b) – F(a) = f(0)х0 + f(1)х1 + … + f(n–1)хn – 1. (3)
Залежність
(3) справджується лише для значень
0, 1, … n,
які задовольняють теорему Лагранжа.
Але коли необмежено збільшувати кількість
n
частин відрізка [a;
b]
так, щоб довжина відрізка хі–1
прямувала до нуля, то рівність (3)
виконуватиметься і різниця F(b)
– F(a)
буде сумою нескінченної кількості
спадних доданків:
![]()
![]()
![]()
![]() (4)
(4)
Рівність (3) справджується не лише за певного, а й за будь-якого вибору точок 0, 1, … n–1, тому (4) є формулою суми нескінченно малих, яку вивели Лейбніц і Ньютон.
