4. Основні методи інтегрування

4.1. Метод безпосереднього інтегрування (мбі)

Одним з найпростіших методів інтегрування є метод безпосереднього інтегрування, який полягає у використанні властивостей НІ та табличних інтегралів.

Приклад 2.

Обчислити невизначені інтеграли

а) ; б);

в) ; г).

Розв’язання

а)

б)

в)

г)

4.2. Метод заміни змінної (мзз)

Суть методу можна сформулювати в наступній теоремі

Теорема 1.1. Нехай функції івизначені на певних проміжках, причомудиференційована. Тоді, якщомає первісну, то справедливо

(*)

Доведення. Оскільки функція визначена, то буде визначеною і первіснаНагадаємо, що похідна від складеної функції обчислюється за формулою

Таким чином, продиференціювавши (*), отримаємо

Остання рівність є правильною в силу означення первісної. Що й потрібно було довести.

Зауваження. На практиці не завжди підінтегральний вираз має класичний (для МЗЗ) вигляд

.

В такому випадку потрібно вводити в розгляд штучну функцію.

Приклад 3.

Обчислити невизначені інтеграли

а) ; б);

в) ; г).

Розв’язання

а)

б)

в)

;

г) .

4.3. Метод інтегрування частинами (міч)

Формула інтегрування частинами дає змогу звести обчислення інтеграла до обчислення більш простого інтегралавикористовуючи формулу

.

Приклад 4.

Обчислити невизначені інтеграли

а) ; б); в).

Розв’язання.

а) .

Для інтеграла покладемо,. Тоді,, маємо

.

Зауваження. Якщо змінна х буде в степені 2, 3, … , то стільки ж разів потрібно застосувати формулу інтегрування частинами.

б) .

Для інтегралафункція, тоді. Звідси, а.

Використовуючи формулу інтегрування частинами , одержимо

.

в) .

Інтеграли такого виду називають циклічними. Для них за и обирають тригонометричну функцію, а за v – експоненту, і інтегрують двічі. Маємо

Отримаємо:

звідки

.

4. Метод інтегрування раціональних дробів (МІРД)

Цей метод використовують під час обчислення інтегралів виду

,

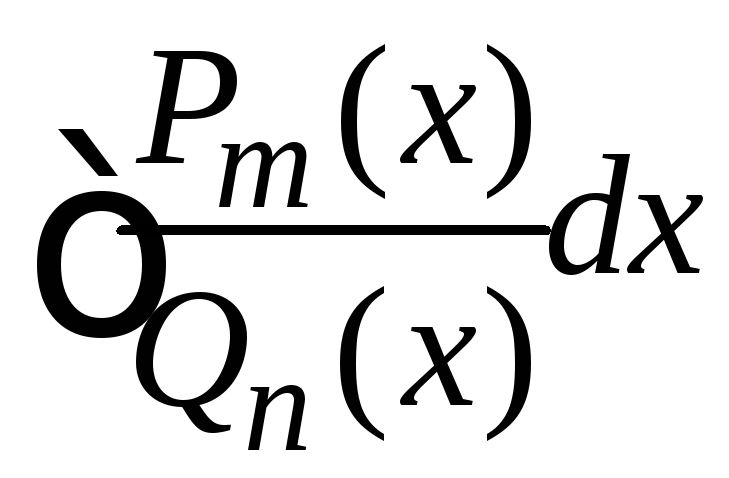де

В залежності від вигляду підінтегральної функції розрізняють наступні способи обчислення інтегралів.

І. Метод внесення під диференціал або МЗЗ

,

ІІ. Використовуючи підстановку ;обчислюють інтеграли виду

.

,

де .

Перший інтеграл обчислюється безпосередньо, а другий за рекурентною формулою

.

ІІІ. Використовується метод невизначених коефіцієнтів для інтегралів виду

І. Якщо

ІІ. Якщо

ІІІ. Якщо

IV. Якщо

(*)

Для знаходження сталих А_і, В_j, C_k..., найчастіше користуються так званим методом невизначених коефіцієнтів. Так, наприклад, зводимо праву частину рівності (*) до спільного знаменника, який дорівнює многочлену Q(х). В результаті з рівності (*) дістанемо два рівні дроби з однаковими знаменниками. Отже, і чисельники цих дро­бів тотожно рівні. В лівій частині рівності чисельником є заданий мно­гочлен R(х), а в правій частині — многочлен від змінної х, коефіцієн­ти якого містять невідомі А_і, В_j, C_k.... Прирівнюючи коефіцієнти при однакових степенях х, дістанемо систему к лінійних алгебраїчних рівнянь, з якої можна визначити шукані невідомі А_і, В_j, C_k...