Приклад 2.

Для функціїу=х²-3х+1 записати формулу Лагранжа на відрізку [1;2] і знайти відповідне значення с.

Розв’язання.

Задана функція є многочленом. А тому вона визначена, неперервна і диференційовна на вказаному відрізку. Таким чином, виконуються умови теореми Лагранжа. Обчислимо значення функції на кінцях відрізка: у(1)=1-3+1=-1, у(2)=4-6+1=-1. Обчислимо значення похідної функції в точці с: у'(с)=2с-3. Тоді 2с-3=2с-3=0 с=1,5.

Наслідок 1. Якщо функція y=f(x) задовольняє умови теореми Лагранжа і похідна цієї функції дорівнює нулю на всьому інтервалі (a;b), то функція є сталою на (a;b).

Наслідок 2. Якщо функції y=f(x) і y=g(x) задовольняють умови теореми Лагранжа і похідні цих функцій рівні між собою на (a;b), то функції відрізняються між собою на константу.

Приклад 3.

Довести, що ,х є [-1; 1]

Розв’язання.

Розглянемо допоміжну функцію,х є [-1; 1]. Функція задовольняє умови теореми Лагранжа на відрізку [-1; 1] і її похідна на інтервалі (-1; 1). За наслідком 1 функція є сталою на інтервалі (-1; 1), тобто arcsin x + +arccosx = c, х є (-1;1). Нехай х=0, тоді arcsin 0 + arccos 0 = cс=.Отже, arcsin x + +arccos x =, х є (-1;1). Безпосередньою перевіркою впевнюємося, що тотожність виконується і для х=1 та х=-1.

4. Теорема Коші.

Теорема 3.4. (Коші). Нехай виконуються умови:

1. функції у=f(x), у=g(x) визначені і неперервні на відрізку [a;b];

2. функції у=f(x), у=g(x) диференційовні на інтервалі (a;b);

3. , х є (a;b),

Тоді існує с є (a;b) така, що ( формула Коші).

Доведення. Розглянемо допоміжну функцію:,х є [a;b]. Ця функція задовольняє умови теореми Ролля, тому існує така точка с є (a;b), що F′(с)=0.

ПРИКЛАД 4.

Знайти значення с із формули Коші для функцій f(x) = x²-2x+3, g(x) = x³-7x²+20x-3, x є [0;1].

Розв’язання.

Задані функції є многочленами, а тому умови теореми Коші виконуються. Обчислимо значення функцій на кінцях відрізка: f(0) = 3, g(0) = -3, f(1) = 2, g(1) = 11. Знайдемо похідні функцій і обчислимо їх значення в точці с: ,.,. Складемо і розв’яжемо рівняння:

, . Вказаному відрізку належитьс₂.

5. Невизначеність виду . Перше правило Лопіталя

Теорема 3.5. (перше правило Лопіталя). Нехай виконуються умови:

1. функції у=f(x) і у=g(x) визначені і неперервні на (a;b] і ;

2. функції у=f(x) і у=g(x) диференційовні на (a;b), ,х є (a;b);

3. існує (скінчена або нескінчена) границя .

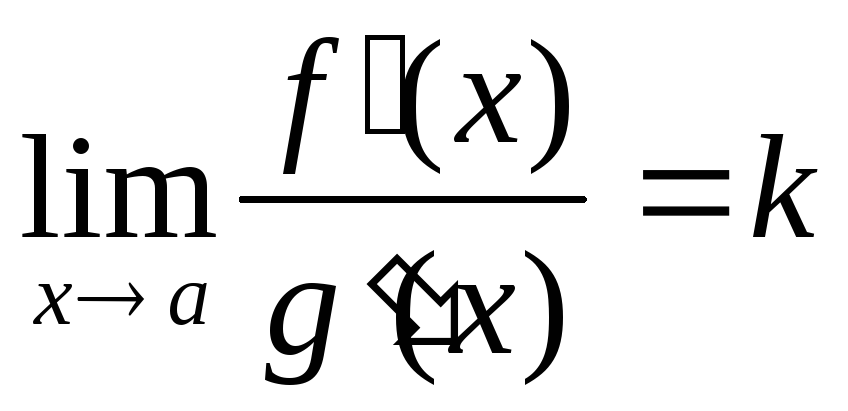Тоді .

Теорема справедлива і тоді, коли а=∞. Крім того, теорему можна застосовувати доти, поки не прийдемо до відношення похідних , яке має певну границю за умови, щоха.

ПРИКЛАД 5.

Обчислити границі:

1) ; 2); 3).

Розв’язання.

1) ;

2);

3) .

6. Невизначеність виду . Друге правило Лопіталя.

Теорема 3.6. (друге правило Лопіталя). Нехай виконуються умови:

1) функції у=f(x) і у=g(x) визначені і неперервні на (a;b] та

2) функції у=f(x) і у=g(x) диференційовні на (а; b) і

3) існує скінчена або нескінчена границя .

Тоді .

ПРИКЛАД 6.

Обчислити границі:

1) ; 2).

Розв’язання.

1);

2)

Обидва правила можна застосовувати декілька разів. Теореми Лопіталя справедливі тоді, коли х є[а;b) х є(а;b), а(або b)=.

7. Невизначеність інших видів.

Зауважимо, що правила Лопіталя застосовуються лише для розкриття невизначеностей виду () і,які називають основними.Розглянемо іншіневизначеності.

1) Невизначеність .Нехай і. Тоді таку невизначеність можна звести до основних:або.

ПРИКЛАД 7.

Обчислити границю .

Розв’язання.

.

2) Невизначеність (). Нехай,і ,.Тоді різницю

f(x)-g(x) можна записати так: .

3) Невизначеність (0⁰), (1^), (⁰).

Розглянемо вираз (f(x))^g(x) i f(x)=g(x)=0. Припускаючи, що f(x)>0, вираз (f(x))^g(x) записують у вигляді (f(x))^g(x)=e^g(x)lnf(x). У показнику при xa маємо невизначеність виду (0·), яка зводиться до невизначеності (). Аналогічно розкриваються невизначеності (1^), (⁰).

ПРИКЛАД 8.

Обчислити границю .

Розв’язання.

Тут невизначеність (0⁰). Маємо: ..

Тема 4. Застосування диференціального числення для дослідження функцій.

1. Монотонність функції.

2. Локальний екстремум функції.

3. Найбільше і найменше значення функції.

4. Опуклість і вгнутість кривих. Точки перегину.

5. Асимптоти кривої.

6. Схема дослідження функції та побудова її графіка.

1. Монотонність функції.

Нехай функція у=визначена на деякому проміжку (а;b).

Теорема 4.1 (необхідна умова монотонності функції). Якщо функція у=диференційовна на інтервалі (а; b) і зростає (спадає) на цьому інтервалі, то її похідна на інтервалі (а;b) невід’ємна (недодатна), тобто

Теорема 4.2 (достатня умова монотонності функції). Якщо функція у=диференційовна на інтервалі (а; b) і ії похідна ) для, то ця функція зростає (спадає) на інтервалі (а; b).

Означення 4.1. Інтервали, на яких функція зростає (спадає), називаються інтервалами монотонності функції.

Отже, щоб знайти інтервали монотонності функції y=f(x),треба:

1) знайти область визначення функції;

2) знайти похідну даної функції;

3) знайти нулі похідної та точки, в яких похідна не існує;

4) розділити точками з пункту 3) область визначення на інтервали, на кожному з них визначити знак похідної. На інтервалах, де похідна додатна, функція зростає, а де від’ємна – спадає.