
- •Границя числової послідовності та функції однієї змінної.
- •Тема 1. Числова послідовність та її границя.
- •1. Числова послідовність та способи її задання.
- •Основні способи задання числової послідовності:
- •2. Обмежені та монотонні числові послідовності.
- •3. Границя числової послідовності.
- •Приклад 1
- •Приклад 2
- •4. Нескінченно малі числові послідовності
- •Властивості нескінченно малих послідовностей
- •Приклад 3.
- •Приклад 4.
- •5. Нескінченно великі числові послідовності
- •6. Арифметичні властивості збіжних числових послідовностей.
- •Приклад 5.
- •Приклад 6.
- •Приклад 7.
- •Приклад 8.
- •Приклад 9.
- •Тема 2. Границя функції неперервного аргументу.
- •1. Означення границі функції за Гейне і за Коші.
- •2. Властивості функцій, які мають границю в точці
- •3. Арифметичні властивості границь функції
- •Теореми про граничні переходи.
- •Приклад 1.
- •Приклад 2.
- •4. Границя функції на нескінченності
- •Приклад 3.
- •5. Перша важлива границя
- •Приклад 4.
- •6. Друга важлива границя
- •Приклад 5.
- •7. Порівняння нескінченно малих функцій. Еквівалентні нескінченно малі функції.
- •Приклад 6.
- •Властивості еквівалентних нескінченно малих функцій.
- •Приклад 7.
- •Тема 3. Неперервність функції.
- •1. Односторонні границі функції.
- •Приклад 1.
- •2. Означення неперервності функції в точці і на проміжку.
- •3. Арифметичні дії над неперервними функціями.
- •4. Одностороння неперервність. Точки розриву та їх класифікація.
- •Класифікація точок розриву
- •Приклад 2.
- •Приклад 3.
- •Приклад 4.
- •5. Властивості функцій, неперервних на відрізку.
- •Диференціальне числення функції однієї змінної.
- •Тема 1: Похідна.
- •1. Задачі, які приводять до поняття похідної.
- •Приклад 1.
- •Приклад 2.
- •2. Означення похідної. Спосіб знаходження похідної. Геометричний та механічний зміст похідної. Рівняння дотичної та нормалі до плоскої кривої.
- •Правило знаходження похідної за означенням.
- •Приклад 4.
- •3. Диференційовні функції. Зв’язок неперервності з диференційовністю
- •Приклад 5.
- •4. Таблиця похідних основних елементарних функцій
- •5. Правила диференціювання.
- •Приклад 6.
- •Приклад 7.
- •Приклад 8.
- •Приклад 9.
- •Приклад 1.
- •2. Властивості диференціала. Інваріантність форми диференціала.
- •Приклад 2.
- •3. Застосування диференціала.
- •Приклад 3.
- •4. Похідні та диференціали вищих порядків. Механічний зміст похідної другого порядку.
- •Приклад 4.
- •Приклад 5.
- •Приклад 6.
- •Тема 3. Теореми про середнє. Правила Лопіталя.
- •1. Теорема Ферма.
- •2. Теорема Ролля.
- •Приклад 1.
- •3. Теорема Лагранжа.
- •Приклад 2.
- •Приклад 3.
- •Приклад 1.
- •2. Локальний екстремум функції.
- •З’ясуємо умови існування локального екстремуму.
- •Приклад 2.
- •Приклад 3.
- •Приклад 4.
- •3. Найбільше і найменше значення функції.
- •Приклад 5.
- •Приклад 6.
- •4. Опуклість і вгнутість кривих. Точки перегину.
- •Приклад 7.
- •5. Асимптоти кривої.
- •Приклад 8.
- •6. Схема дослідження функції та побудова її графіка.
- •Приклад 9.
- •Інтегральне числення функції однієї змінної
- •Тема 1. Невизначений інтеграл
- •Поняття первісної та невизначеного інтегралу
- •Приклад 1.
- •Властивості невизначеного інтеграла (ні).
- •4. Основні методи інтегрування
- •4.1. Метод безпосереднього інтегрування (мбі)
- •Приклад 2.
- •4.2. Метод заміни змінної (мзз)
- •Приклад 3.
- •4.3. Метод інтегрування частинами (міч)
- •Приклад 4.
- •Цей метод використовують під час обчислення інтегралів виду
- •Приклад 5.
- •Загальне правило інтегрування раціональних дробів.
- •Приклад 6.
- •Він зводиться до інтеграла від раціональної функції підстановкою . Приклад 7.
- •Обчислити
- •Обчислити
- •Обчислити
- •Обчислити
- •4.6. Біноміальний диференціал
- •Приклад 8.
- •4.7. Інтегрування тригонометричних функцій
- •Приклад 10.
- •Поняття визначеного інтеграла.
- •2. Властивості визначеного інтеграла.
- •4. Теорема Ньютона-Лейбніца (н-л)
- •Приклад 1.
- •5. Методи знаходження ві.
- •5.1. Метод безпосереднього інтегрування
- •Приклад 2.
- •5. 2. Метод заміни змінної
- •Приклад 3.
- •Приклад 4.
- •5.3. Метод інтегрування частинами
- •Приклад 5.
- •Приклад 6.
- •Формули зведення. Формула інтегрування частинами
- •Приклад 7.
- •Приклад 2.
- •Приклад 3.
- •Площа криволінійного сектора
- •Приклад 4.
- •3. Обчислення довжини дуги
- •Приклад 5.
- •Приклад 6.
- •Обчислення тиску рідини на вертикальну пластину
- •9. Невласні інтеграли із нескінченним проміжком інтегрування
- •Приклад 10.
- •Приклад 11.
- •Обчислення невласних інтегралів від розривних (необмежених) функцій
- •Приклад 12.
2. Означення похідної. Спосіб знаходження похідної. Геометричний та механічний зміст похідної. Рівняння дотичної та нормалі до плоскої кривої.
Нехай
задано функцію
![]() .
Точка
.
Точка![]() .
Надамо точціх0
приросту
.
Надамо точціх0
приросту
![]() х
так, щоб точка
х
так, щоб точка
![]() .
Знайдемо приріст функції в точціх0:
.
Знайдемо приріст функції в точціх0:
![]() .
.
Означення
1.1. Якщо
існує скінчена границя при
![]() х
що прямує до 0, відношення приросту
функції до приросту аргументу, то її
називаютьпохідною
функції
f(x)
в точці х0.
х
що прямує до 0, відношення приросту
функції до приросту аргументу, то її
називаютьпохідною
функції
f(x)
в точці х0.
Похідна
функції
![]() в точціх0
позначається одним із таких символів:
в точціх0
позначається одним із таких символів:
![]() ;
;
![]() |
|![]() ;
;![]() |
|![]() ;
;![]()
Таким
чином, за означенням
![]() (1.3)
(1.3)
Якщо
розглядати похідну функцію в конкретній
точці х0,
то отримаємо число; якщо розглянути
похідну функцію в кожній точці відрізка
[a;b],
то отримаємо функцію, яку позначатимемо
![]() .
.
Правило знаходження похідної за означенням.
Розглядаємо точку х0 і надаємо їй довільного приросту
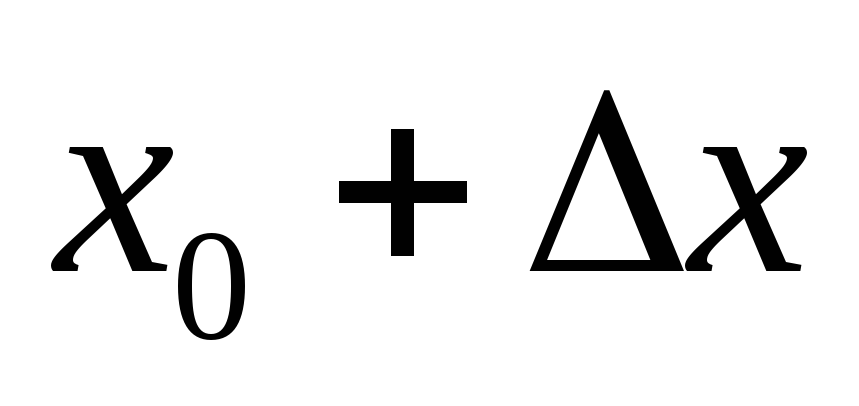 .
.Шукаємо приріст функції в т. х0:
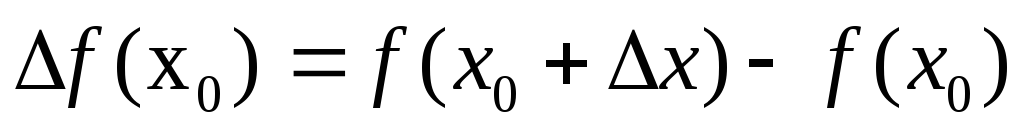 .
.Шукаємо відношення приросту функції до приросту аргументу:

Обчислюємо границю і якщо вона існує, то вона є похідною функції в даній точці:

ПРИКЛАД 3.
Знайти за означенням похідну функції:
а)
![]() в точціх0
= 1, б)
в точціх0
= 1, б)
![]() в точціх0
= 0.
в точціх0
= 0.
Розв’язання.
а)
![]() в точціх0
= 1
в точціх0
= 1
1.
![]()
2.
![]()
3.
![]()
4.
![]()
б)
![]() в точціх0
= 0.
в точціх0
= 0.
1.
![]()
2.
![]()
3.
![]()
4.
Таким чином, не існує
![]() ,
а тому функція
,
а тому функція![]() в т.х
= 0 похідної немає.
в т.х
= 0 похідної немає.
Із
формул (1.1) і (1.3) слідує, що величина
миттєвої швидкості – це похідна від
пройденого шляху ![]() за
часом t:
v=
за
часом t:
v=![]() . В цьому
полягає фізичний
або механічний зміст похідної.
У загальному випадку, яку б залежність
не відображала функція
. В цьому
полягає фізичний
або механічний зміст похідної.
У загальному випадку, яку б залежність
не відображала функція
![]() ,
,![]() можна
розглядати якмиттєву
швидкість зміни функції.
можна
розглядати якмиттєву
швидкість зміни функції.
Із
формул (1.2) і (1.3) слідує, що кутовий
коефіцієнт дотичної до кривої
![]() в точціМ0(х0;y0)
– це похідна
в точціМ0(х0;y0)
– це похідна
![]() в цій точці:k=tgσ=
в цій точці:k=tgσ=![]() .
У цьому полягаєгеометричний
зміст похідної.
.
У цьому полягаєгеометричний
зміст похідної.
Знайдемо
рівняння дотичної. Оскільки відомий
кутовий коефіцієнт дотичної і точка
М0(х0;y0),
через яку
проходить дотична, то маємо: y-y0=![]() (x-x0).
Знайдене рівняння називають рівнянням
дотичної до
кривої
(x-x0).
Знайдене рівняння називають рівнянням
дотичної до
кривої
![]() в точці
М0(х0;y0).
Якщо ж функція в точці М0
має нескінченну похідну, то це означає,
що дотична в цій точці паралельна осі
Оу, а
її рівняння таке: х=х0.
в точці
М0(х0;y0).
Якщо ж функція в точці М0
має нескінченну похідну, то це означає,
що дотична в цій точці паралельна осі
Оу, а
її рівняння таке: х=х0.
Нормаллю
до кривої називається
пряма, яка проходить через точку дотику
перпендикулярно до дотичної. Кутові
коефіцієнти дотичної і нормалі пов’язані
умовою: kдот·kнорм=-1.
Тоді kнорм=![]() ,тобто
kнорм=
,тобто
kнорм=![]() .Рівняння
нормалі до
кривої
.Рівняння
нормалі до
кривої
![]() в точціМ0(х0;y0)
має вигляд: у-у0=
в точціМ0(х0;y0)
має вигляд: у-у0=![]() (х-х0).
(х-х0).
Приклад 4.
Скласти рівняння дотичної і нормалі до кривої у=2х2+1 у точці М0(1;3).
Розв’язання.
Знайдемо
похідну функції і обчислимо її значення
для х=1.
у'=4х,
звідки у'(1)=4.
Рівняння дотичної: у-3
= 4(х-1)
![]() у=
4х-1.
Рівняння нормалі: у-3=
у=
4х-1.
Рівняння нормалі: у-3=![]()
![]() у
=
у
=![]() .
.
3. Диференційовні функції. Зв’язок неперервності з диференційовністю
Означення
1.2.
Якщо функція
![]() має похідну в т.х0,
то кажуть, що функція диференційовна в
цій точці.
має похідну в т.х0,
то кажуть, що функція диференційовна в
цій точці.
Якщо функція диференційовна в кожній точці [a;b], то кажуть, що вона диференційовна на відрізку [a;b].
Приклад 5.
Довести,що функція f(x)=x2+6 диференційовна на R.
Розв’язання.
Виберемо
довільну точку х0![]() R і доведемо існування похідної заданої
функції в цій точці. Знайдемо приріст
функції:
R і доведемо існування похідної заданої
функції в цій точці. Знайдемо приріст
функції:
![]() f(x0)=(x0+
f(x0)=(x0+![]() x)2+6-x02-6=x02+2x0
x)2+6-x02-6=x02+2x0![]() x+
x+![]() x2-x02-6=2x0
x2-x02-6=2x0![]() x+
x+![]() x2=
x2=![]() x(2x0++∆x).
Обчислимо границю
x(2x0++∆x).
Обчислимо границю
![]() Таким
чином, в точціх0
існує похідна,
а, отже, функція диференційована в цій
точці. Оскільки точка х0
– довільна
точка, то функція диференційовна на R.
Таким
чином, в точціх0
існує похідна,
а, отже, функція диференційована в цій
точці. Оскільки точка х0
– довільна
точка, то функція диференційовна на R.
Теорема 1.1. (про зв’язок неперервності з диференційовністю). Якщо функція y = f(x) диференційовна в т. х0, то вона неперервна в цій точці.
Доведення.
Нехай функція
y = f(x)
диференційовна в точці
![]() Тоді існує
Тоді існує![]() .
Приріст можемо записати так:
.
Приріст можемо записати так:![]() .
Тоді
.
Тоді![]() .
За означенням неперервної функції в
точці маємо, що функція
.
За означенням неперервної функції в
точці маємо, що функція![]() в
т.х0
– неперервна.
в
т.х0
– неперервна.
Зауваження.
Із неперервності функції в точці, взагалі
кажучи, не випливає її диференційовність.
Наприклад, функція
![]() в т.х0
– неперервна, але вона і цій точці не є
диференційовною.
в т.х0
– неперервна, але вона і цій точці не є
диференційовною.
