1.3.3. Теорема гіпотез (формулиБейєса)

Ця теорема є наслідком теореми множення ймовірностей.

Теорема.  Нехай подіїH_k(k1,...,n)утворюють повну систему подій (P(H_k)>0). Тоді для будь-якої події A (P(A)>0) виконується співвідношення

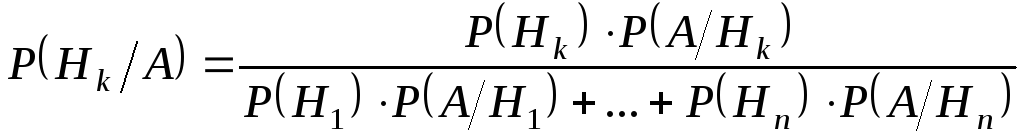. (7)

Доведення.Оскільки, то на підставі формули (5) одержимо

.

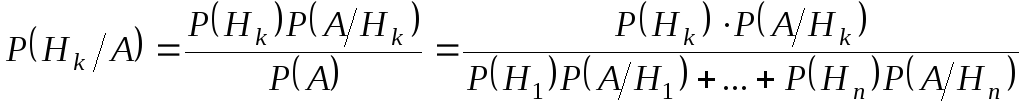Події H_kприйнято називатигіпотезами,P(H_k) - апріорними (відомими до проведення випробування), а P(H_k/A) - апостеріорними (обчисленими після випробування) ймовірностями цих гіпотез.

Приклад 1. В умовах прикладу 1 пункту 1.3.2 на приймальному кінці каналу одержано сигнал "0". Яка ймовірність того, що було послано сигнал "1"?

Розв’язок. Апріорна ймовірність гіпотези H₁ (до випробування) дорівнює 1 – p₀, а її апостеріорна ймовірність P(H_k/A) (після випробування) знаходиться за формулою (7)

.

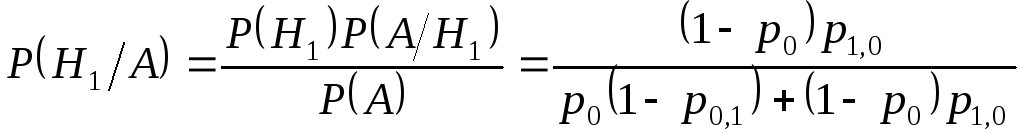Приклад 2. Надійність приладів (ймовірність безвідмовної роботи протягом заданого проміжку часу) в залежності від якості одного з елементів дорівнює відповідно 0.95, 0.9, 0.85. Відомо, що 30% приладів випускають у першому варіанті, 25% – у другому і 45% – у третьому. Довільно вибраний прилад безвідмовно працював протягом заданого проміжку часу. Яка ймовірність, що він був виконаний в кожному з варіантів?

Розв’язок. Позначимо через A подію, яка полягає у безвідмовній роботі приладу. Нехай гіпотеза H_k(k1,...,n) означає, що прилад виконано уk-му варіанті. Тоді апріорні ймовірності гіпотез та умовні ймовірностіA дорівнюють:

P(H₁)0.3, P(H₂)0.25, P(H₃)0.45,

P(A/H₁)0.95, P(A/H₂)0.9, P(A/H₃)0.85.

За формулою Бейєса знаходимо апостеріорні ймовірності гіпотез

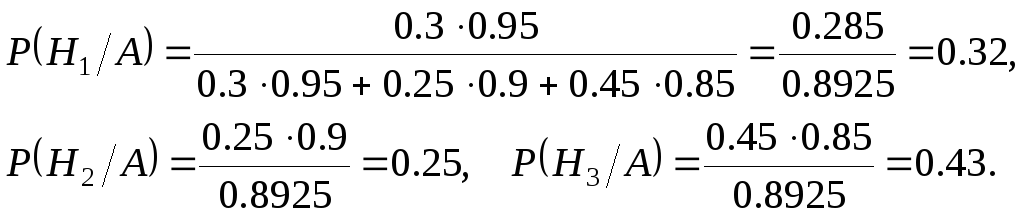
Приклад 3. Двоє стрільців роблять по одному пострілу. Ймовірність попадання по мішені для першого стрільця – 0.7, а для другого – 0.8. У мішені знайдено одну пробоїну. Яка ймовірність того, що у мішень попав перший стрілець?

Розв’язок. Подія A означає наявність однієї пробоїни в мішені. Введемо гіпотези H₁– обидва стрільці не попадають,H₂– перший стрілець попадає, другий ні,H₃– другий стрілець попадає, перший ні,H₄– обидва стрільці попадають. Знайдемо апріорні ймовірності гіпотез:

P(H₁)0.3·0.20.06, P(H₂)0.7·0.20.14,

P(H₃)0.3·0.80.24, P(H₄)0.7·0.80.56.

Умовні ймовірності події A дорівнюють:

P(A/H₁)0, P(A/H₂)P(A/H₂)1, P(A/H₄)0.

Таким чином, апостеріорна ймовірність гіпотези H₂ така:

.

1.4. Випробування із скінченною кількістю наслідків

1.4.1. Класичне означення ймовірності

Розглянемо випробування, простір якого складається з Nточок (випробування із скінченою кількістю наслідків). Якщо ймовірності елементарних подій відомі, то ймовірність будь-якої подіїA у випробуванні можна знайти підсумовуючи ймовірності тих елементарних подій, які сприяють A. Найчастіше симетріяумов випробування забезпечує рівну можливість різних елементарних подій (наприклад, при підкиданні грального кубика рівно можливі всі шість елементарних подій). У таких випробуваннях ймовірність однієї елементарної події визначається їх загальною кількістю. Дійсно, із виразу₁+₂+...+_Nвиходить рівність 1P(₁+P(₂+...+ +P(_N  N·P(_i на підставі якої одержимо

.

Теорема.Якщо у випробуванні з рівно можливими елементарними подіями подіїA сприяють M елементарних подій, то

. (1)

Доведення.Оскільки подіїAсприяютьMелементарних подій, то

.