1.2.2. Аксіоми ймовірності та її властивості.

Означення 1. Ймовірністю називається числова функція P(A), визначена на множині всіх подій, пов’язаних з даним експериментом, яка задовольняє таким аксіомам:

1. P(A)  0;

2. P(  1

3. P(A₁ A₂) = P(A₁) + P(A₂), якщо A₁  A₂ .

Аксіома 3 допускає узагальнення на випадок суми скінченої (або зліченої) кількості попарно несумісних подій:

3. P(A₁A₂A₃...A_n) = P(A₁)+P(A₂)+P(A₃)+...+P(A_n). (1)

Із аксіом 1,2,3 випливають такі властивості ймовірностей:

1) P()1–P(A); 2) 0P(A)1

3) Теорема додавання ймовірностей.Для будь-яких подійA та B справедливе співвідношення

P(AB)P(A)+P(B) – P(AB). (2)

Д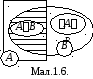оведення.Подамо подіїAB та B у вигляді суми попарно несумісних подій (мал.1.6) BAB , ABA. Тоді на підставі аксіоми 3 одержимо P(AB)=P(A)+ +P() і P(B)P(AB)+P(). Підставляючи вираз P() із другого співвідношення в перше, приходимо до рівності (2).

1.2.3. Принцип практичної вірогідності

Застосування результатів теорії ймовірності грунтується на такому принципі: якщо ймовірність настання події Aдостатньо близька до 1, то при одноразовому проведенні випробування слід знехтувати можливістю настання подіїA. У цих умовахAтаAназивають відповідно практично вірогідною та практично неможливою подіями.

Визначення тієї межі, починаючи з якої подію слід вважати практично неможливою, знаходиться за рамками теорії ймовірностей. Ясно, що чим більші збитки може принести нехтування можливості настання події, тим меншою повинна бути межа. Наприклад, межа 0.001 достатня для того, щоб вважати практично неможливим перегорання нової електричної лампочки, але абсолютно недопустима для того, щоб вважати практично неможливою аварію на АЕС. (Збитки, до яких може привести один із тисячі випадків незрівнянно вищі, ніж вигода, одержана у 999 випадках).

1.3. Теорема множення та її наслідки

1.3.1. Умовна ймовірність

Нехай А та B є подіями, пов’язаними з деяким випробуванням і P(B)0.

Означення 1. Умовною ймовірністю P(АB) події А за умови здійснення події B називається відношення

. (1)

Властивості умовної ймовірності аналогічні властивостям ймовірностей 1-3 пункту 1.2.2.

Із співвідношення (1) випливає теорема множення ймовірностей

. (2)

Якщо P(A)0, то теорема множення може бути записана у вигляді

. (2)

Ця теорема дозволяє знайти ймовірність перерізу (добутку) подій, якщо із змісту задачі зрозумілі (легко обчислюються) значення умовних ймовірностей.

Приклад 1. Ймовірність аварії при запуску ракети дорівнює 0,15. Ймовірність аварії на старті є 0,12. Яка ймовірність аварії при умові успішного старту.

Розв’язок. Нехай подія A полягає у тому, що запуск ракети успішний, а подія B - це успішний старт ракети. Із умов задачі випливає, що A·B=A. Отже,

Таким чином, P(/B)1–P(A/B)0.034.

Означення 2. Подія А називається незалежною від події B, якщо P(АB)P(А)   (P(B)0).

Нехай подія А незалежна від події B і P(A)0. Тоді з формул (2) та (2) випливає, що подія B незалежна від події А. Таким чином, поняття незалежності подій є взаємним.

Події А та B незалежні тоді і тільки тоді, коли виконується рівність

. (3)

Якщо події А та B незалежні, то будуть незалежними такі пари подій: А та B; А таB;А таB.

У тому випадку, коли кількість подій перевищує два, вводиться поняття незалежних у сукупності подій. Останнє означає, що ймовірність якої-небуть події не залежить від здійснення інших. Наприклад, для трьох подій А₁, А₂, А₃, незалежних у сукупності, повинні виконуватись співвідношення P(A₁/A₂)P(A₁), P(A₁/A₃)P(A₁), P(A₁/A₂·A₃)P(A₁), P(A₂/A₃)P(A₂), P(A₂/A₁·A₃)P(A₂), P(A₃/A₁·A₂)P(A₃). Для подій А₁, А₂,..., А_n, незалежних у сукупності, справедливе співвідношення

. (3)

Приклад 2. Проводиться два постріли по мішені. Ймовірності попадання при першому та другому пострілі дорівнюють відповідно 0.3 і 0.6. Яка ймовірність, що у мішені буде: а) точно одна пробоїна; б) хоча б одна пробоїна?

Розв’язок. Позначимо через A_i (i=1,2) подію, яка полягає у тому, що при i–му пострілі буде попадання у мішень. Події A₁ та A₂ незалежні, але сумісні.

а) Нехай A – подія , яка полягає у тому, що у мішені буде точно одна пробоїна. Тоді . Оскільки подіїінесумісні, то на підставі аксіоми 3 і теореми множення ймовірностей одержимо

б) Нехай B – подія , яка полягає у тому, що в мішені буде хоча б одна пробоїна. Тоді B=A₁+A₂  і на підставі теорема додавання і множення ймовірностей матимемо

Інший спосіб розв’язку:

Приклад 3. Для умов прикладу 1 пункту 1.1.2 знайти ймовірність безвідмовної роботи (надійність) схеми, елементи якої виходять із ладу незалежно один від іншого з ймовірностями рівними відповідно 1– p_i (i1,2,3). Яка схема надійніша при умові p_i p (i1,2,3)?

Розв’язок. Зрозуміло, що події A_i, які розглядаються в прикладі, незалежні у сукупності.

а) На підставі теорем додавання та множення ймовірностей одержимо:

P(A) P(A₁·A₂)+P(A₃) – P(A₁·A₂·A₃)P(A₁)·P(A₂)+P(A₃) – P(A₁)·P(A₂)·P(A₃)

 p₁·p₂+p₃ – p₁· p₂· p₃.

б) Аналогічно знаходимо

P(A) P(A₁)·P(A₂+A₃) P(A₁)·[P(A₂)+P(A₃) – P(A₂)·P(A₃)] 

 p₁·(p₂+p₃ – p₂· p₃).

Більш надійною є перша схема, оскільки при p (0;1)

p²+p – p³ > 2p² – p³.

Відмітимо, що при знаходженні ймовірності суми сумісних подій доцільно переходити до протилежної події.

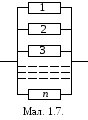
Приклад 4. Система (мал.1.7) складається зnпаралельно з’єднаних елементів, які виходять з ладу протягом деякого проміжку часу незалежно один від одного з ймовірностями 1 – p_i (i1,…,n). Знайти ймовірність безвідмовної роботи (надійність) системи.

Розв’язок. Нехай подія A_i (i1,…,n) означає, що i-тий елемент не вийшов з ладу (справно працює). Позначимо через Aподію, яка полягає у безвідмовній роботі системи. Оскільки система безвідмовно працює лише тоді, коли працює хоча б один її елемент, тоA  A₁A₂...A_n. Перейдемо до події, протилежноїA (система виходить з ладу, якщо перестали функціонувати всі її елементи): . Оскільки подіїA_i незалежні у сукупності, то

P(A)  1 – P()  1 –   1 – (1 – p₁)...(1 – p_n).

Внаслідок того, що 1 – p_i < 1, одержаний результат узгоджується з допущенням про зростання надійності системи при зростанні n.

Використаємо результат прикладу 4 для того, щоб знайти найменше число однотипних елементів, необхідних для забезпечення заданої надійності P системи:

P 1 – (1 – p)ⁿ  n  lg(1 – P) / lg(1 – p) +1, (4)

де a – найбільше ціле число, менше від a.