3.Числові характеристики випадкових величин

3.1. Математичне сподівання та його властивості

3.1.1. Стійкість середнього арифметичного

Повнуінформацію про випадкову величину дає її розподіл ймовірності. Проте часто експериментатор не володіє такою інформацією, та вона і не є необхідною. Досить охарактеризувати випадкову величину кількома числами. Найчастіше використовують дві характеристики випадкової величини – математичне сподівання (інакше, середнє значення) та дисперсію.

Нехай випадкова величина Xприймає відповідно значенняx₁, x₂,…, x_mз ймовірностямиp₁, p₂,..., p_m. Проведемо серію зn випробувань, в кожному з яких будемо спостерігати значення випадкової величини. Припустимо, що в цій серії випадкова величинаX прийнялаn_kраз значенняx_k(k=1, 2,..., m). Складемо середнє арифметичне результатів спостереження випробувань

.

Середнє арифметичне є випадковою величиною, оскільки воно залежить від конкретної серії випробувань і від n. Однак, із властивості стійкості частоти (n_k / n  p_k при достатньо великомуn) випливає властивість стійкості середнього арифметичного (при зростанніnсереднє арифметичне коливається поблизу деякого числа):  x₁·p₁+x₂· p₂+ ...+x_m·p_m.

3.1.2. Математичне сподівання випадкової величини

Означення 1.Математичним сподіваннямвипадкової величиниXназивається числоMX, яке в залежності від типу випадкової величини визначається формулою

(1)

Математичне сподівання дає уяву про розташування значень випадкової величини.

Розмірність математичного сподівання MXспівпадає з розмірністю випадкової величиниX.

Приклад 1. Нехай подіяAз’являється у випробуванні з імовірністюp. Знайти математичне сподівання числа появ подіїAв даному випробуванні.

Розв’язок. Позначимо число появ подіїAу випробуванні черезX. ВеличинаX –випадкова, приймає свої значення 0 і 1 з імовірностями 1– pтаp. Тоді на підставі формули (1) (верхній рядок) одержимо

MX=0·(1– p)+1·p.

Приклад 2. Знайти математичне сподівання випадкової величиниX, розподіленої по закону Пуассона з параметром(розділ 2.1, формула (5)).

Розв’язок. Оскільки (k=0,1,...) , то згідно з формулою (1) маємо

.

Приклад 3. Знайти математичне сподівання випадкової величиниX, розподіленої за показниковим законом з параметром(розділ 2.1, формула (8)).

Розв’язок. На підставі формули (1) (нижній рядок) одержимо

.

Звідси виходить, що середній проміжок часу Tміж двома послідовними відмовами апаратури дорівнює 1/, якщо тривалість проміжку часу між двома послідовними відмовами апаратури розподілена за показниковим законом з параметром. З цієї причини показниковий розподіл у теорії надійності записується у вигляді

,

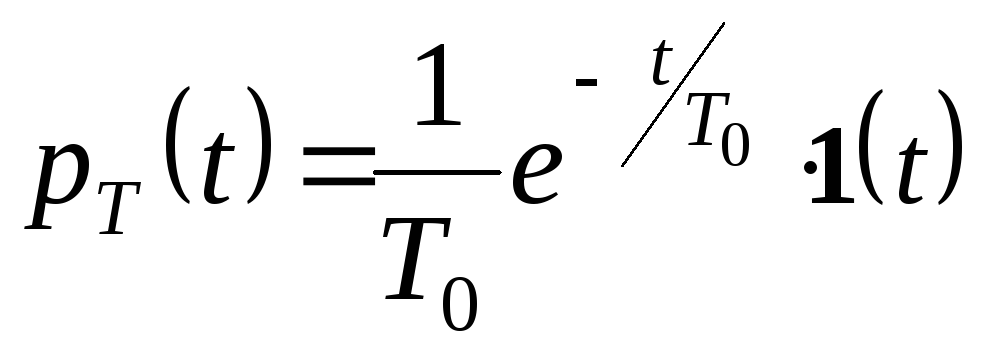де T₀‑ середній час роботи до відмови.

П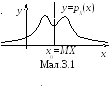ри обчисленні математичного сподівання доцільно використовувати такий результат.

Теорема 1. Якщо розподіл випадкової величиниX симетричний відносно прямоїx=x₀, тоMX=x₀ (мал.3.1).

Наслідки: 1) Математичне сподівання випадкової величини, розподіленої по закону Гауса N(a; ²), дорівнює a.

2) Математичне сподівання рівномірного у проміжку [c; d] розподілу дорівнює (c+d)/2.

3) Математичне сподівання випадкової величини, розподіленої за законом Стьюдента _n, дорівнює 0.

Приклад 4. Знайти математичне сподівання випадкової величини, розподіленої за законом Релея з параметром² (розділ 2.2, формула (11)).

Розв’язок. За формулою (1) маємо

.