3.2.2. Дисперсія суми випадкових величин

Теорема. 1) Якщо випадкові величини X та Y корельовані (отже, залежні), то

D(X+Y)=DX+DY+2K(X,Y); (4)

2) Якщо випадкові величини XтаY незалежні (отже, некорельовані), то

D(X+Y)=DX+DY. (5)

^{Доведення.}

1) D(X+Y )= =

=DX+DY+2K(X,Y);

2) незалежність  K(X,Y)=0.

Рівність (5) має місце для будь-якого скінченого числа незалежних (отже, попарно некорельованих) випадкових величин:

D(X₁+X₂+...+X_n)=DX₁+DX₂+...+DX_n. (5´)

Зокрема, якщо всі випадкові величини X_iмають однаковий розподіл і незалежні, то D(X₁+X₂+...+X_n)=nDX₁і внаслідок цього

.

Останній результат означає, що при великій кількості незалежних вимірювань (випробувань) середнє арифметичне результатів спостереження буде близьким до вимірюваної величини.

Приклад 1. Нехай випадкові величиниX₁,...,X_nнезалежні і однаково розподілені (зокрема,MX_i=a,DX_i=²(i=1,..., n)). Знайти математичне сподівання і дисперсію випадкової величини .

Розв’язок. Використовуючи властивості математичного сподівання (формули (3) і (6) розділу 3.1) і дисперсії (формули (3) і (5)) одержимо

(тут незалежність випадкових величин не грає ніякої ролі),

.

Таким чином, відхилення випадкової величини від математичного сподіванняaіз зростаннямnспадає, при цьому її значення =(x₁+x₂+…+x_n) ⁄n(середнє арифметичне результатів спостережень) приблизно дорівнюєa.

Приклад 2. Знайти дисперсію випадкової величиниX- кількості появ подіїA у серії зn незалежних випробувань.

Розв’язок. Застосуємо метод, використаний при розв’язанні прикладу 1 пункту 3.1.4, використаємо (5‘) і результат прикладу 1 пункту 3.2.1. ОскількиX=X₁+X₂+...+X_n, де незалежні випадкові величиниX_i приймають значення0,1 з імовірностями відповідно 1–p, p, то DX=DX₁+DX₂+...+DX_n= =nDX₁= np(1–p).Звідси випливає, що дисперсія частотиX/nпояв подіїAтака

.

Приклад 3. В умовах прикладу 2 пункту 3.1.4 знайти дисперсію випадкової величини.

Розв’язок. На підставі (5‘) і результату прикладу 3 пункту 3.2.1Dη=n ∕ λ².

Приклад 4. В умовах прикладу 1 знайти математичне сподівання випадкової величини .

Розв’язок. Перетворимо суму до зручного для обчислень вигляду:

Тому

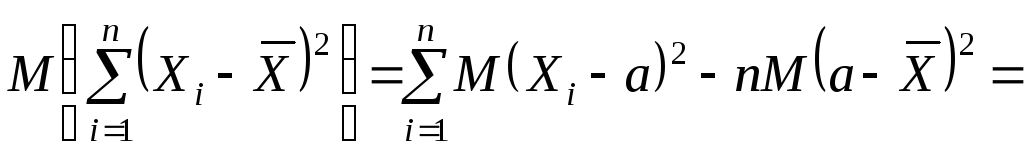
і, таким чином,

.

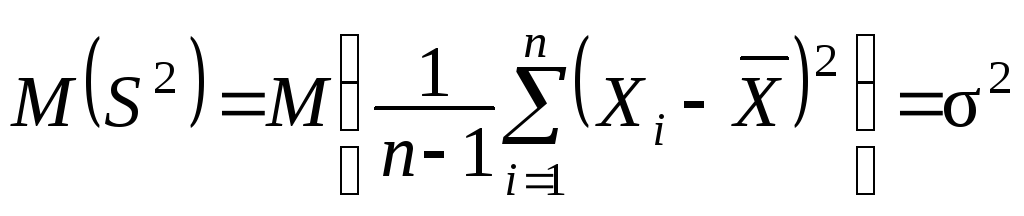Можна показати, що D(S ²) із зростаннямn прямує до нуля. З урахуванням одержаного вище результату, це означає, що числа , які є значеннями випадкової величиниS ²у конкретних серіях вимірювань, групуються навколо числа².

Приклад 5. Нарівні з середнім квадратичним відхиленням мірою розсіювання випадкової величини є такожсереднє відхилення- математичне сподівання модуля флуктуації:

.

Знайти середнє відхилення випадкової величини XN(a;²).

Розв’язок.

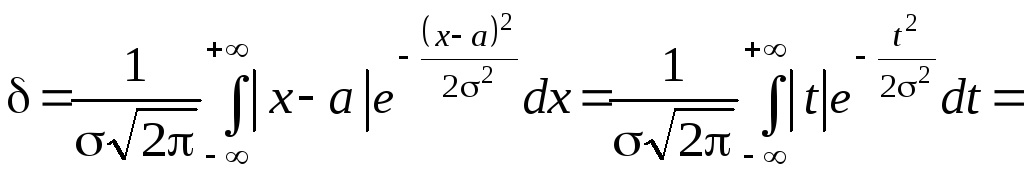
3.2.3. Нерівність п.Чебишева

Нерівність П.Чебишева встановлює верхню межу для ймовірності відхилення випадкової величини від її математичного сподівання. А саме (мал.3.3),

. (6)

Ця оцінка ймовірності не залежить від закону розподілу випадкової величини X. Із (6) видно, що чим менше DX, тим менш ймовірні великі відхилення t_X значень випадкової величини від математичного сподівання.

Поклавши в (6) t=3, одержимо

 .

Нерівність Чебишева, як правило, завищує ймовірності великих відхилень. Наприклад, для закону Гауса

P{X[a–3; a+3]}=1–P{X[a–3; a+3]}=1– Ф(3)=0.0027.

Однак, можна навести приклади розподілів, для яких вона дає точну величину ймовірності відхилення (наприклад, P{X=-1}=P{X=1}=1/18, P{X=0}=8/9, t=3).

Приклад 1. Оцінити з допомогою нерівності Чебишева ймовірність відхилення частоти появи подіїA в серії зn випробувань Я.Бернуллі від ймовірностіpпояви події в одному випробуванні.

Розв’язок. Математичне сподівання і дисперсія чистотиX/nпояви події були знайдені відповідно у прикладах 1 пункту 3.1.4 та 2 пункту 3.2.2:M(X/n)=p,D(X/n)=p(1– p)/n. Отже, на підставі нерівності (6) одержуємо

.

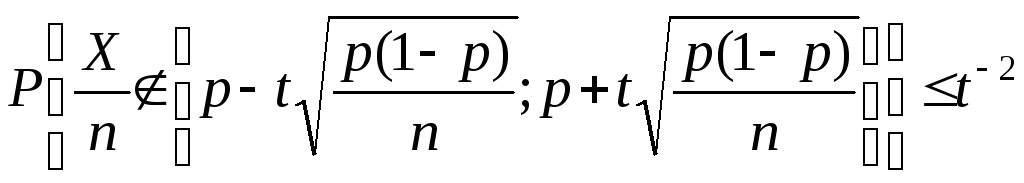Оскільки p(1–p)1/4, то з попередньої нерівності виходить грубіша оцінка

. (7)

При достатньо великому t>0права частина останньої нерівності як завгодно мала. Таким чином, довільно малою є ймовірність відхилення частоти подіїA від ймовірностіpна величину більшу за . Вибираючиnдостатньо великим, це відхилення можна зробити як завгодно малим. Інакше кажучи, при достатньо великомуnзначне відхилення частоти від ймовірності є практично неможливим. Це виправдовує підхід до визначення ймовірностіpяк деякого числа, навколо якого групуються частоти (див. пункт 1.2.1).

Нерівність (7) можна використати для розв’язку задачі перевірки гіпотези(докладно ця задача обговорюється у розділі 5.4).

Перевірка гіпотези. Нехай ймовірністьpпояви події Aв одному випробуванні невідома, а кількість появ подіїAу даній серії зn випробувань Я.Бернуллі дорівнюєk. Висунемо гіпотезу (припущення), що невідома ймовірність дорівнюєp₀. Наскільки добре ця гіпотеза узгоджена з результатами експерименту? В основу розв’язку цієї задачі покладено такий принцип:якщо у даному випробуванні відбувається подія, яка при зробленому припущенні є практично неможливою, то це припущення суперечить результатам експерименту.

Вибираємо мале число  >0(рівень значущості) і вважаємо практично неможливими події, ймовірність яких менша. Із (7) виходить, що для практично неможливої події і допустиме відхилення значення частоти від ймовірності дорівнює . Якщо одержане в експерименті відхилення| k/n–p₀| перевищує допустиме, то висунута гіпотеза суперечить результатам експерименту.