1.3.2. Формула повної ймовірності

Часто для вивчення випробування, з яким пов’язана подіяA, корисно ввести до розгляду події H_k, для яких із тих чи інших міркувань відомі ймовірності P(H_k), P(A/H_k).

Теорема. Нехай подіїH_k (k1,...,n) складають повну систему. Тоді для будь-якої події Aсправедлива рівність

P(A)  P(H₁)·P(A/H₁) + ... + P(H_n)·P(A/H_n). (5)

Доведення. Оскільки H₁H₂...H_n, то подію A можна представити у вигляді суми попарно несумісних подій A  A·H₁A·H₂...A·H_n (мал.1.8).

Послідовно застосовуючи теореми додавання та множення ймовірностей (формули (1) розділу 1.2 та формули (2) розділу 1.3), одержимо:

.

Якщо P(H_i)0, то відповідна складова у сумі повинна бути опущена.

Інколи формулою повної ймовірності називають співвідношення

P(A)  P(A·H_i).

Приклад 1. По каналу зв’язку можуть передаватись з ймовірностями, рівними p₀ та p₁ 1 – p₀, два сигнали – "0" та "1". Внаслідок дії перешкод можливі викривлення сигналів: "0" переходить в "1" з імовірністю p_0,1, а "1" в "0" з імовірністю p_1,0 (мал.1.9). Яка ймовірність одержати на приймальному кінці каналу сигнал "0"?

Розв’язок. Розглянемо припущення: H₀ – послано сигнал "0", H₁ – послано "1". Нехай подія A – це одержання сигналу "0". Тоді P(A/H₀)1 – p_0,1, P(A/H₁)p_1,0, P(H₀)p₀, P(H₁)1 – p₀. З формули повної ймовірності (9) маємо: P(A)  p₀ (1 – p_0,1) + (1 – p₀) p_1,0.

Приклад 2. Система складається з п’яти незалежних елементів, з’єднаних так, як показано на мал.1.10.а). Знайти надійність (ймовірність безвідмовної роботи) системи, якщо надійність k-го елемента дорівнює p_k.

Р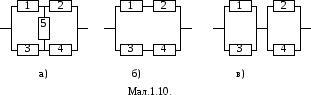озв’язок. Нехай подія A означає, що система працює безвідмовно. Розглянемо такі припущення: H₁ – п’ятий елемент працює безвідмовно, H₂ – п’ятий елемент виходить з ладу. Надійність системи при умові безвідмовної роботи п’ятого елемента – P(A/H₁) – співпадає з надійністю системи, зображеної на мал.1.10.в). Отже, на основі результату прикладу 2.б) пункту 1.3.1, одержимо:

P(A/H₁)  (p₁+p₃ – p₁·p₃)·(p₂+p₄ – p₂·p₄).

Якщо п’ятий елемент виходить з ладу, то надійність системи – P(A/H₂) – співпадає з надійністю системи, зображеної на мал.1.10.б). Скористаємося результатом прикладу 2.а) пункту 1.3.1:

P(A/H₂)  p₁·p₂+p₃·p₄ – p₁·p₂·p₃·p₄.

Оскільки за умовою задачі P(H₁)  p₅ , а P(H₂) 1– p₅, то за допомогою формули повної ймовірності знаходимо:

P(A)  p₅·(p₁+p₃ – p₁·p₃)·(p₂+p₄ – p₂·p₄)+(1 – p₅)·(p₁·p₂+p₃·p₄ – p₁·p₂·p₃·p₄).

У тому випадку, коли всі елементи працюють з однаковою надійністю (p_ip): P(A)  p²·(2+2p – 5p²+2p³).

Зауваження.Припустимо, що деяка система може знаходитись в одному з станів E₁, E₂,...,E_n (наприклад, система, що складається з двох однотипних пристроїв, які відразу після виходу з ладу починають ремонтувати, може знаходитись в одному з чотирьох станів: E₁ – обидва пристрої працюють, E₂ – перший ремонтується, другий працює, E₃ – другий ремонтується, перший працює, E₄ – обидва ремонтується). Позначимо через E_k(s) подію, яка означає, що на момент часу s система знаходиться у стані E_k. Припустимо, що умовні ймовірності P(E_j(t+s)/E_k(s)) переходу системи із стану E_k в мом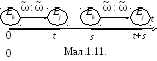ент часуs в стан E_j в момент часу t+s залежать тільки від тривалості проміжку часу [s; t+s] і не залежать від його положення на осі часу (мал.1.11). Назвемо ці умовні ймовірності перехідними ймовірностями системиі введемо позначення

P(E_j(t+s)/E_k(s)) = p_kj(t), s0, t>0.

Скористаємося формулою повної ймовірності для виведення рівняння, якому задовольняють перехідні ймовірності.

О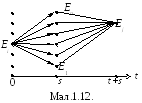скільки подіїE₁(s), E₂(s),..., E_n(s) складають повну систему, то перехід від стану E_i в момент часу 0 у стан E_j в момент часу t+s можна виконати nспособами (мал.1.12):

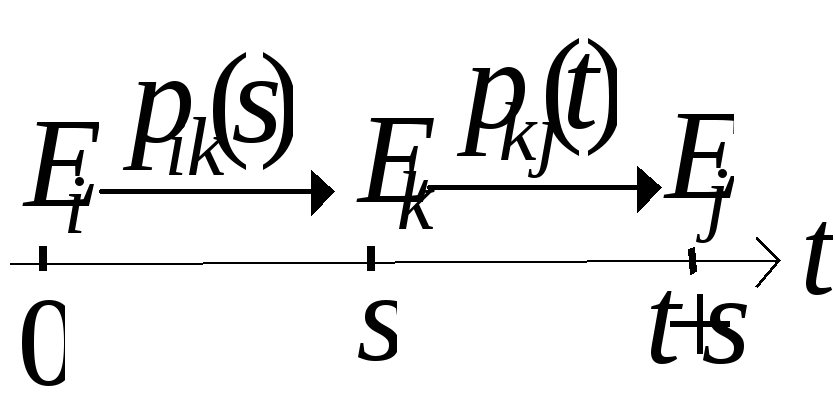
Будемо вважати, що поведінка системи на проміжку часу [s; t+s] визначається її станом на момент часу s і не залежить від поведінки системи на проміжку часу [0; s]. Оскільки стан E_i системи у початковий момент часу не впливає на перехід системи із стану E_k в момент часу s в стан E_j в момент часу t+s, то

.

Застосуємо тепер формулу повної ймовірності:

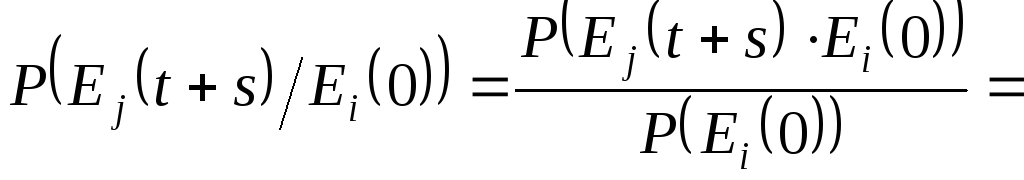
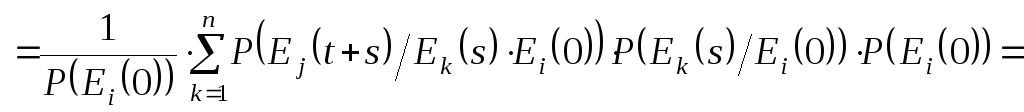
Таким чином, перехідні ймовірності задовольняють рівнянню Колмого­рова-Чепмена

. (6)