2.1.2. Дискретні випадкові величини

Випадкова величина Xназиваєтьсядискретною, якщо: 1) сукупність її можливих значень можна перерахувати –x₁, x₂,..., x_n(абоx₁, x₂,..., x_n,...); 2) можна знайти відповідні ймовірностіp_k = P{X = x_k} того, що випадкова величинаXприймає ці значення.

Набір ймовірностей p_k називають розподілом випадкової величини X. Розподіл містить вичерпну інформацію про випадкову величину. Якщо у проміжок[c; d)попадають лише значенняx_i, x_i+1,..., x_jвипадкової величиниX, то подіяX[c; d)є сумою попарно несумісних подійX= x_i, X= x_i+1,…, X=x_j. Тому на підставі формули (1) розділу 1.2 одержимо:

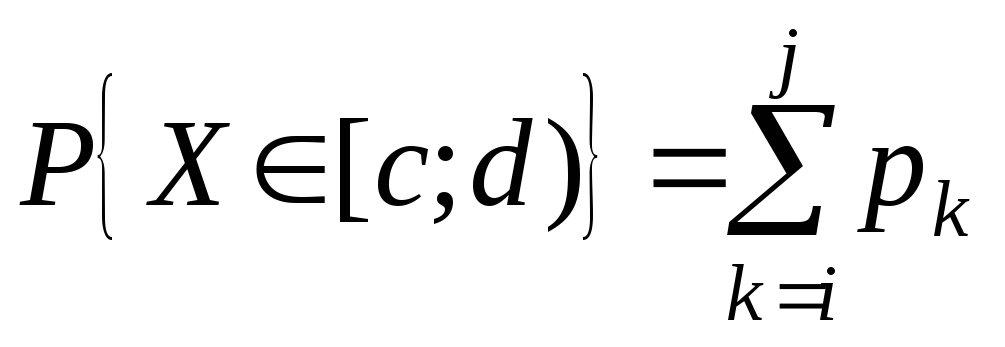. (3)

І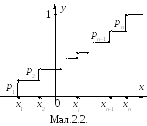з формули (3) виходять такі наслідки:

1) 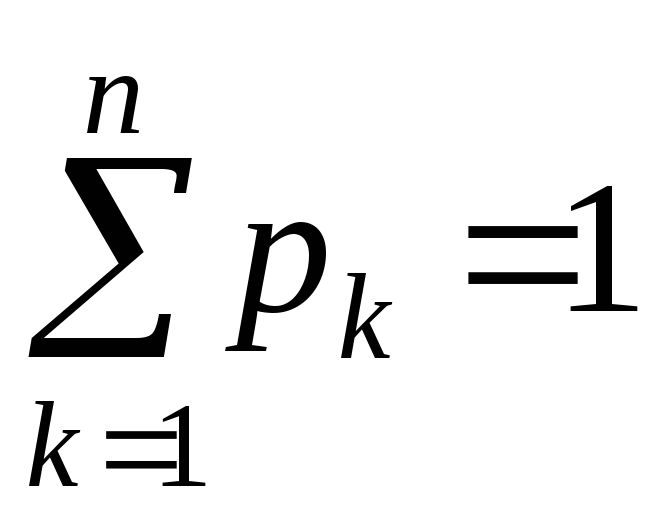– умова нормування;

2) F_X (x) =  p_k, де знак суми стосується лише тих значеньk, для якихx_k < x. Звідси випливає, що значення функції розподілу дискретної випадкової величини у проміжку (x_k; x_k+1] дорівнюєp₁+p₂+...+p_k. Приблизний графік функції розподілу дискретної випадкової величини зображено на мал.2.2.

Відзначимо слідуючий факт: будь-яка сукупність чисел p_k  0, таких, що p_k = 1, визначає розподіл деякої випадкової величини.

Приклад 1. Дискретна випадкова величинаXзадається таблицею розподілу

X	-1	0	2	5
P	0.3	0.1	a	0.35

Знайти: 1) a; 2)F_X (x); 3)P{X > – 0.3}; 4)P{X≤ 1.7}.

Розв‘язок. 1) Значення a знаходиться із умови нормування:

0.3+0.1+a+0.35=1a=0.25.

2) Функцію розподілу знаходимо на основі наслідку 2, а її графік приведено на мал.2.3.

3) P{X > – 0.3} = P{X = 0} + P{X = 2} + P{X = 5} = 0.7.

4) P{X≤ 1.7} = P{X = 0} + P{X = – 1} = 0.4.

Розглянемо кілька найбільш важливих дискретних розподілів.

1) Біноміальний розподіл (розподіл Я. Бернуллі).Випадкова величинаXприймає значення 0,1,...,nі при цьому

. (4)

Біноміальний розподіл має випадкова величина, що дорівнює кількості появ подіїA у серії зnнезалежних випробувань при ймовірностіpїї появи в одному експерименті. На малюнку 2.4.а) наведено графік біноміального розподілу приn=20,p=0.5.

2) Геометричний розподіл.Випадкова величинаXприймає значення 0,1,... і при цьомуp_k = p(1– p) ^k–1(k =1,2,...). Геометричний розподіл має випадкова величина, що дорівнює кількості повторень випробувань до першої появи подіїA при ймовірностіpїї появи в одному експерименті.

3) Рівномірний дискретний розподіл.Випадкова величинаXприймаєnзначень з відповідними ймовірностями, що дорівнюють 1/n(мал.2.4.б).

4) Розподіл Пуассона.Випадкова величинаXприймає значення 0,1,... з ймовірностями

. (5)

На малюнку 2.4.в) наведено графік розподілу Пуассона з параметром =1.5. На підставі формули (2) розділу 1.5 кількість рідкісних подій має розподіл Пуассона.

2.1.3. Неперервні випадкові величини

Випадкова величина Xназиваєтьсянеперервною, якщо: 1) множина її значень співпадає з проміжком (кількома проміжками) числової осі; 2) ймовірність того, що випадкова величина набуває будь-якого наперед заданого значенняx₀дорівнює нулю:P{X= x₀}= 0 (взагалі кажучи, із 2) випливає 1)). Зауважимо, що хочаP{X=x₀}=0, подіяX=x₀є можливою.

Випадкові величини, описані вище у прикладах 3), 4), 5) пункту 2.1.1, є неперервними.

Означення 1.Невід’ємна функціяp_X(x)називаєтьсящільністю ймовірності(щільністю розподілу) випадкової величиниX,якщо ймовірність попадання випадкової величини у довільний проміжок [x₀; x₀+x) малої довжини приблизно дорівнює p_X (x₀)·x:

P{X[x₀; x₀+x)} ~ p_X (x₀)·x (x0). (6)

Таким чином, число p_X (x₀)·x характеризує долю тих випробувань у достатньо довгій серії, в яких випадкова величина X попадає у проміжок [x₀; x₀+x).

Щільність ймовірності p_X(x)випадкової величиниXмає розмірність, обернену доX.

Щільність ймовірності p_X (x)випадкової величиниX має таку характерну властивість, яку сформулюємо у вигляді теореми.

Теорема.Ймовірність попадання неперервної випадкової величиниXу проміжок [c; d) знаходиться за формулою

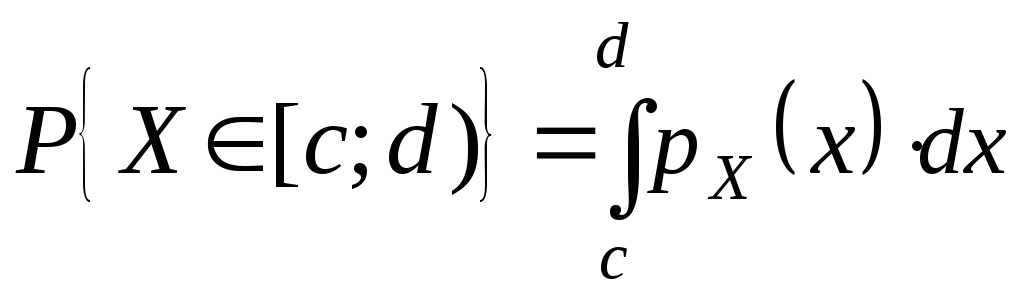. (7)

Для доведення формули (7) потрібно розбити проміжок [c; d) на велику кількість відрізків[x_k; x_k+1) малої довжиниx_k (відрізки не перетинаються). Ймовірність попадання випадкової величиниX у проміжок[x_k; x_k+1) на підставі (6) приблизно дорівнюєp_X (x_k)x_k. Підсумовуючи ці ймовірності і переходячи до границі приmax x_k 0, одержуємо формулу (7). У лівій частині формули (7) можна замінити проміжок [c; d) на [c; d], (c; d). Геометричний зміст теореми дає малюнок 2.5.

Із співвідношення (7) випливають такі наслідки:

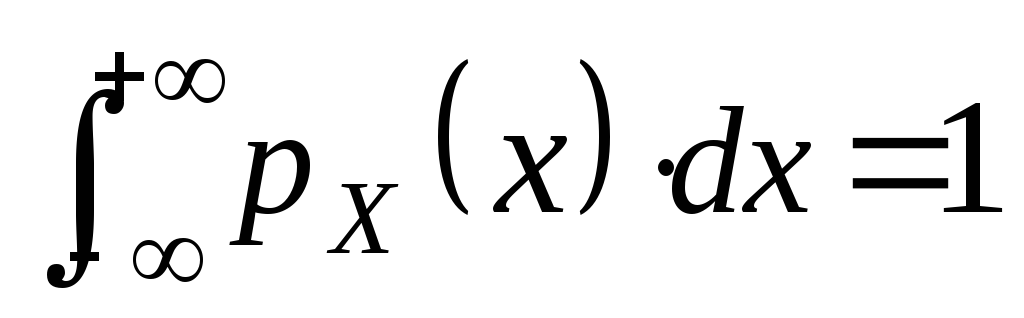1. (умова нормування);

2. .

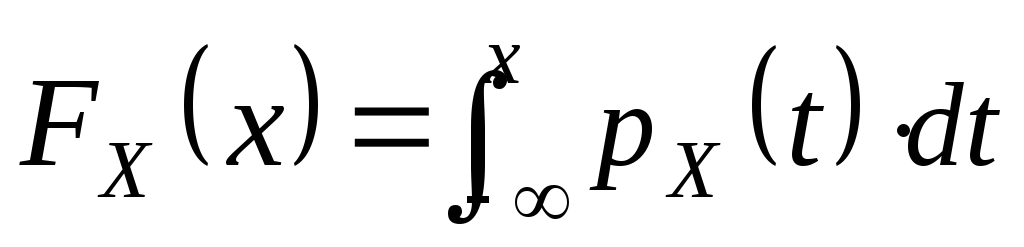Наслідок 2) у точках неперервності функціїp_X (x)має таку еквівалентну форму запису:

.

Функція розподілу неперервної випадкової величини є неперервною кусково-гладкою функцією. Характерний вигляд функції розподілу приведено на мал.2.6.

Приклад 1. Щільність ймовірності неперервної випадкової величиниXмає вигляд

Знайти: 1) a; 2)F_X (x); 3)P{X[1 ∕ 3; 4]} .

Розв’язок. 1) Коефіцієнт a знаходимо із умови нормування:

.

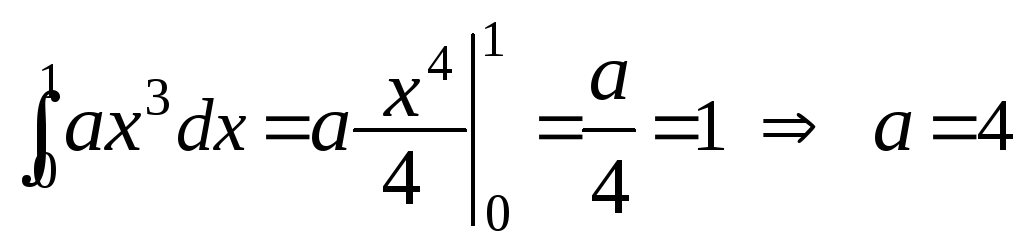
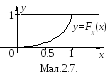2)

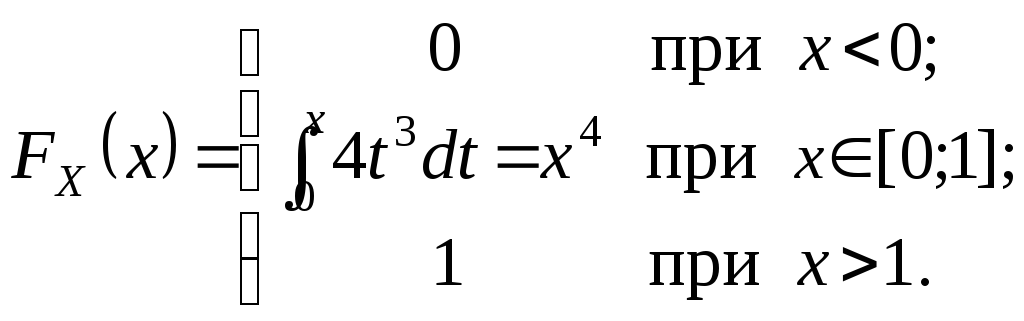
Графік функції розподілу приведено на мал.2.7.

3) .

Розглянемо деякі найбільшважливі неперервні розподіли.

1) Рівномірний (прямокутний) розподіл.Випадкова величинаXрівномірно розподілена у проміжку [c ; d], якщо її щільність ймовірності має вигляд (мал.2.8.а):

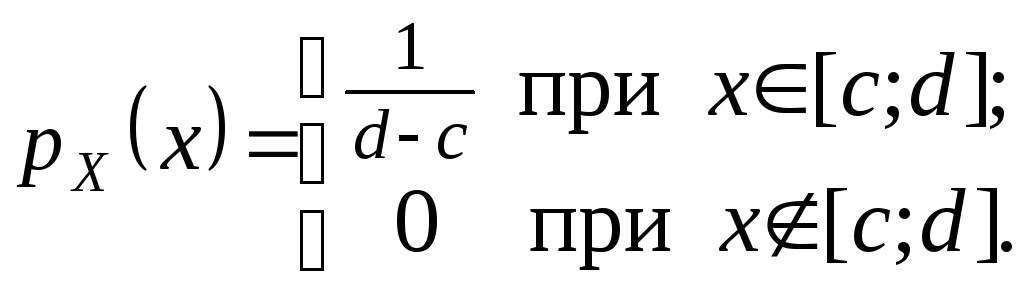
Цей розподіл є неперервним аналогом класичного означення ймовірності (відповідає припущенню про довільний вибір точки у проміжку [c ; d]). Графік функції розподілу приведено на мал.2.8.б.

Якщо при вимірюванні результат округляється до найближчого цілого значення, то помилка вимірювання є неперервною випадковою величиною, яка рівномірно розподілена у проміжку [– 0.5 ; 0.5].

Помилка, яка допускається при округленні числа з точністю до 10^-m, рівномірно розподілена у проміжку [– 0.5·10^-m ; 0.5·10^-m].

2) Показниковий розподіл.Випадкова величинаXмає показниковий розподіл з параметром>0, якщо її щільність розподілу

, (8)

де 1(x)=– одинична функція.

Відповідна функція розподілу має вигляд

.

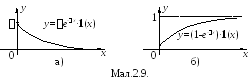
Графіки щільності ймовірності та функції розподілу приведені на мал.2.9.а і 2.9.б.

Показниковий розподіл (і тільки він серед неперервних розподілів) має властивість «відсутності післядії»:

P{X > x₁+ x₂ ⁄ X > x₁} = P{X > x₂} (x₁,  x₂ > 0).

Дійсно,

Зауваження.Нехай кількість відмов приладу на проміжку часу [0 ; t] розподілена за законом Пуассона з параметромt:

і випадкова величина T –тривалість проміжку часу між двома послідовними відмовами приладу (мал.2.10). Тоді випадкова величинаTрозподілена за показниковим законом з параметром:

p_T (t) =λe^–λt ·1(t).

Дійсно,

F_T (t) =P{T< t} =1–P{T ≥ t}.

Оскільки подія T  tозначає, що на проміжку [0 ; t] прилад працює безвідмовно, тоP{T  t} = p₀(t) =e^–λt. Отже,

F_T (t) =1–e^–λt(t ≥0)

і, таким чином,

.

В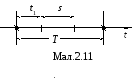ластивість відсутності післядії приводить до того, що ймовірність безвідмовної роботи приладу протягом проміжку часу тривалістюsне залежить від того, який проміжок часуt₁прилад уже пропрацював (мал.2.11).

Функцією надійності P(t)називаєтьсяймовірністьP{T ≥ t} безвідмовної роботи приладу протягом проміжку часуt:

P(t)= P{T ≥ t}=1– P{T < t}=1–F_T (t).

Таким чином, функція надійності дорівнює P(t)=e^–λt·1(t), якщо відмови апаратури розподілені за законом Пуассона.

У деяких задачах (пов’язаних із старінням апаратури) вважають, що випадкова величина T– тривалість проміжку часу між двома послідовними відмовами приладу розподілена за законом Вейбулла-Гнеденко (приr =1 одержуємо показниковий розподіл). У цьому випадку функція надійності P(t) має вигляд:

P(t)=.

3) Нормальний (Гаусів) розподіл.Випадкова величинаXмає нормальний розподіл з параметрамиa та ², якщо її щільність розподілу має вигляд (мал.2.12.а):

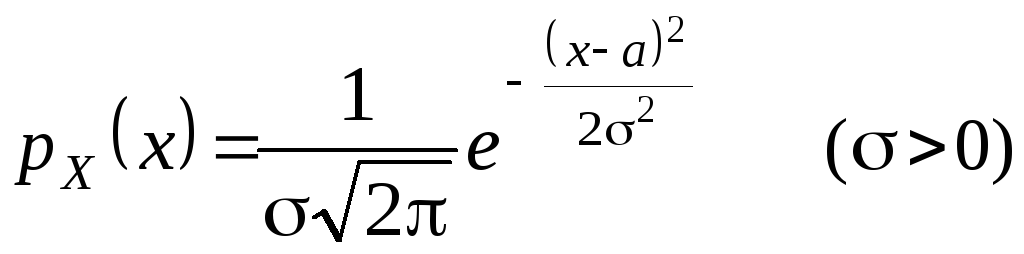. (9)

У подальшому запис XN(a;²) означатиме, що випадкова величинаXмає розподіл Гауса з параметрамиa та ². Графік розподілу Гауса є симетричним відносно прямоїx=a. Єдиний максимум досягається приx=aі дорівнює . Оскільки площа під графіком дорівнює 1, то при зменшенні графік стає більш «високим» та «вузьким».

Функція розподілу випадкової величини XN(a;²) виражається через функцію Лапласа Ф(x) (пункт 1.5.2). Дійсно,

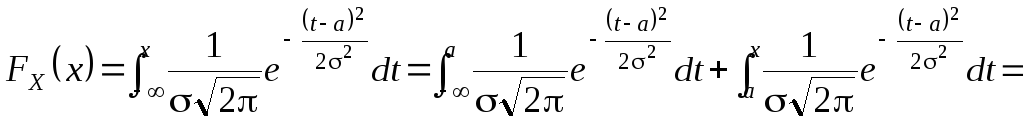
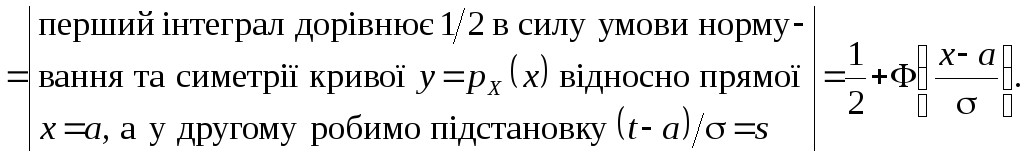
Г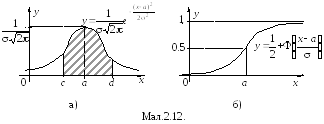рафік функції розподілу приведено на мал.2.12.б.

Розподіл Гауса відіграє фундаментальну роль в застосуваннях теорії ймовірності.

Оскільки ймовірність попадання випадкової величини у проміжок дорівнює різниці значень функції розподілу на кінцях проміжку, то

. (10)

Якщо проміжок [c;d] довжиною 2sрозташований симетрично відносно точкиx=a, то формула (10) набирає особливо простого вигляду

. (10)

Зокрема, ймовірність попадання у проміжок [a-3;a3] дорівнює 0.9973. Таким чином, можна стверджувати, що подія {X[a-3;a3]} є практично неможливою. У цьому полягає знамените правило «трьох сигм».

Приклад 2. Відхилення розміру деталі від стандартного розподілено за законом N(0;16 мм²). Деталь вважається придатною, якщо відхилення від стандарту не перевищує 6мм. Який відсоток випуску непридатних деталей?

Розв’язок. Нехай випадкова величина X – відхилення розміру деталі від номінального. Знайдемо ймовірність того, що деталь буде забраковано

Таким чином, брак складає майже 13.5%.