2.2.3. Неперервний випадковий вектор

Випадковий вектор називаєтьсянеперервним, якщо його координатиX таYє неперервними випадковими величинами (іншими словами, ймовірність попадання у будь-яку наперед фіксовану точку дорівнює нулю). У цьому випадку існує невід’ємна функція –щільність ймо­вір­ності випадкового вектора –така, що ймовірність попадання випадкового вектора у довільний малий прямокутник П{[x₀; x₀+Δx), [y₀; y₀+Δy)} (мал.2.17) має вигляд

. (3)

Співвідношення (3) дозволяє довести, що ймовірність попадання вектора в будь-яку область площини Dзнаходиться за формулою

. (4)

Із співвідношення (4) випливають такі наслідки:

1. (умова нормування, яка означає, що об’єм тіла, обмеженого поверхнею та площиною , дорівнює одиниці);

2. .

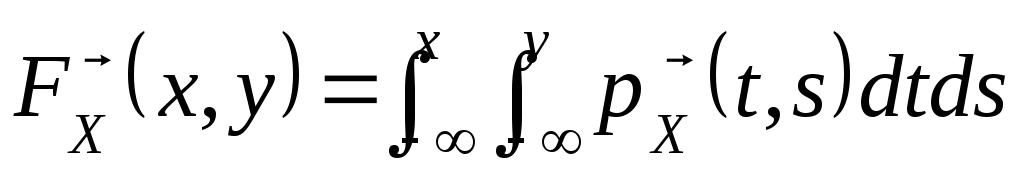Оскільки і , то із наслідку 2 знаходимо вираз для щільностей ймовірності координат через щільність ймовірності вектора (умови узгодженості)

(5)

Відновити щільність ймовірності випадкового вектора за щільностями ймовірності його координат можна не завжди.

Умовна щільність ймовірності p_X (x /Y=y)випадкової величиниX при умовіY=y визначається співвідношенням

. (6)

Останнє співвідношення можна записати у вигляді, подібному до теореми множення ймовірностей

. (6')

Випадкова величина X називається незалежною від випадкової величиниY, якщо при всіх значенняхx,yвиконується рівністьp_X (x / Y=y)=p_X (x). Із (6) виходить, що поняття незалежності є взаємним. Випадкові величиниX таYнезалежні тоді і тільки тоді, коли справедливе співвідношення

. (7)

Якщо випадкові величини X таYне є незалежними, то вони називаютьсязалежними. Ця залежність може бути або функціональною –Y=g(X), або мати імовірнісний (стохастичний) характер, коли значення, яке приймає одна величина лише впливає на закон розподілу іншої.

У іншому випадку мова може йти лише про наближене представлення випадкової величини Yфункцією випадкової величиниX:

Yg(X).

При цьому функція g(X) вибирається так, щоб звести до мінімуму (в якомусь сенсі) похибку цієї наближеної рівності.

Приклад 1. Випадковий вектор розподілений в областіD{(x;y): 0<x<1, x<y<1} з щільністю ймовірності . Знайти: 1) ко­ефіцієнтA; 2) щільності ймовірності координат; 3) умовні щільності ймовірності; 4) ймовірність попадання в областьD₁{(x;y): 0<x<1/2,x<y<1–x}.

Розв’язок. 1) Виходячи з умови нормування одержуємо (мал.2.18.а)

;

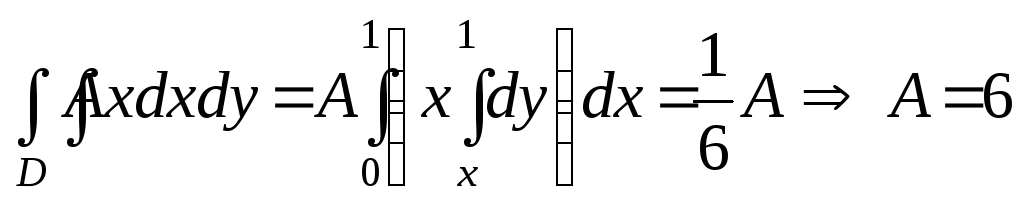
2) Із умов узгодженості (5) одержуємо

, якщо x[0;1],

, якщо y[0;1].

3) На підставі формули (6) та результатів пункту 2 знаходимо:

, якщо 0<x<y,y(0;1),

, якщоx<y<1,x(0;1).

Випадкові величини X таY є залежними.

⁴⁾ (мал.2.18.б).

Проінтегрувавши рівність (6') по зміннійyта скориставшись умовою узгодженості (5), знайдемо аналог формули повної ймовірності

. (8)

2.2.4. Найважливіші види двовимірних розподілів.

1) Рівномірний розподіл.Випадковий вектор називається рівномірно розподіленим у областіD, якщо

S -площа областіD.

Я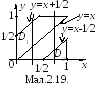кщо двовимірний вектор рівномірно розподілений у прямокутнику зі сторонами, паралельними осям координат, то координатиX таYбудуть незалежними рівномірно розподіленими випадковими величинами. Наведемо приклад залежних величин, які самі і у сукупності розподілені рівномірно.

Приклад 1. Нехай випадковий вектор рівномірно розподілений в областіD=D₁D₂ (мал. 2.19). Знайти щільності ймовірності координат вектора.

Розв’язок. Сума площ фігур D₁іD₂дорівнює 1/2 (половина площі квадрата із стороною 1) і тому

На підставі умов узгодженості (формула (5) розділ 2.2), маємо

Таким чином, випадкова величина X рівномірно розподілена на відрізку [0;1]. Аналогічно доводиться, що випадкова величина Y також рівномірно розподілена на відрізку [0;1]. Оскільки p_X(x)p_Y(y), то випадкові величиниX таYбудуть залежними.

Приклад 2. Випадкові величиниX таYнезалежні і розподілені рівномірно у проміжку [0;1]. Знайти ймовірність того, що корені квадратного рівнянняXx²+x+Y=0 дійсні.

Розв’язок. Невід’ємність дискримінанта рівносильна умові X·Y. Вектор рівномірно розподілений у квадраті D{(x; y): 0 x1, 0 y1} і тому _{Таким чином,}

.

Область інтегрування D₁розташована у квадратіDвище гіперболиxy=1/4(див.мал.2.20).

2) Двовимірний нормальний розподіл.Випадковий вектор називається розподіленим за нормальним законом (законом Гауса) з параметрамиa₁, a₂, ₁², ₂²,r, якщо його щільність розподілу має вигляд:

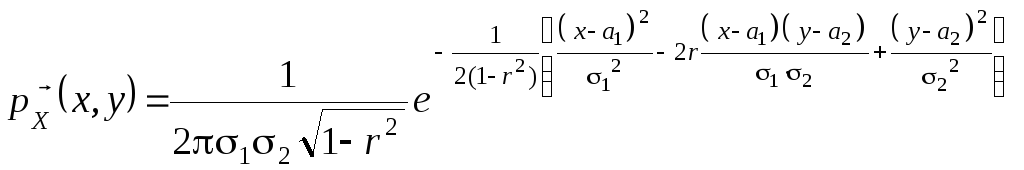, (9)

де r <1,₁>0, ₂>0.

При r0 із (9) одержуємо двовимірний закон Гауса в найпростішій формі

. (10)

Функція , визначена рівністю (9), набуває максимального значення у точці (a₁;a₂), яка називається центром розсіювання, і постійне значення на еліпсах

.

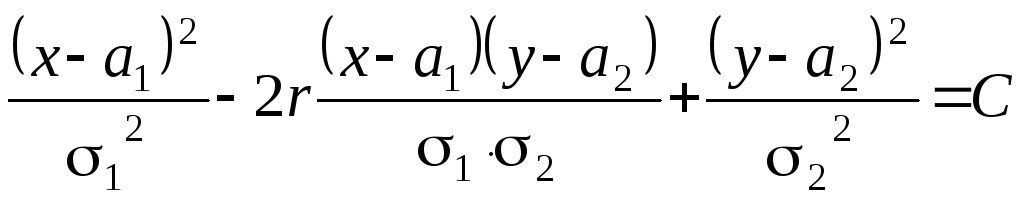Ці еліпси, що називаються еліпсами рівної ймовірності або еліпсами розсіювання, дають уявлення про форму повер­хні . Приr=0 і ₁=₂еліпси перетворюються в кола, а приr 1 стають «витягнутими» і «тон­кими». Біль­ша вісь еліпса повернута на кут відносно осіOx (мал.2.21).

З розподілу (9) виходить, що випадкові величини XтаYрозподілені за законами ГаусаXN(a₁;₁²) таYN(a₂;₂²). Проте, добуток цих законів дає не розподіл (9), а (10). Тому координати двовимірного випадкового вектора, розподіленого за законом Гауса у найпростішій формі, є незалежними випадковими величинами, а за законом Гауса у загальній формі – залежними. Умовні щільності ймовірності також є Гаусовими. Наприклад, умовна ймовірність

співпадає з .

Ймовірність попадання випадкового вектора в область ефективно може бути знайдена тоді, коли r = 0 і областьD є прямокутником з сторонами, паралельними осям координат, або колиD‑ область, обмежена еліпсом розсіювання.

Приклад 3. Гармата обстрілює злітно-посадочну смугу шириною 60м та довжиною 200м. Координати точки попадання снаряда по відношенню до системи координат, осі якої направлені вздовж та поперек смуги, а початок знаходиться у її центрі (мал.2.22), розподілені за законом

.

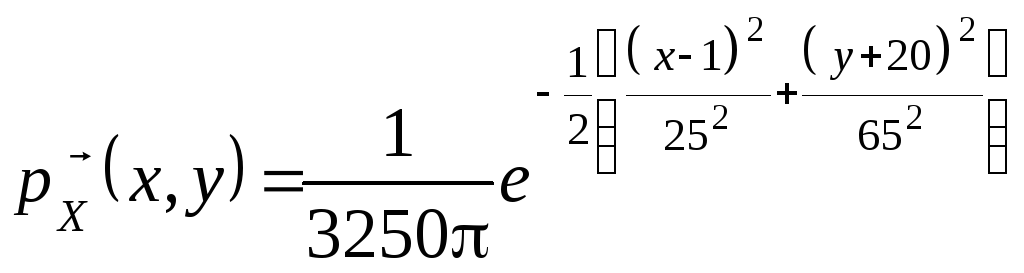Знайти ймовірність попадання у смугу при одному пострілі.

Розв’язок. (Випадкові величини X та Y незалежні). Оскільки XN(1м; 25² м²),YN(–20м;65² м²), то на підставі формули (10) розділу 2.1 одержуємо

.

Отже, ймовірність попадання у смугу дорівнює 0.66.

3) Розподіл Релея.Нехай випадковий вектор розподілений за законом Гауса у найпростішій формі (10) з параметрамиa₁=a₂=0, ₁²=₂²=².

Тоді випадкова величина – відстань від точки (X;Y) до початку координат – розподілена за законом Релея з параметром² (графік щільності приведено на мал.2.23):

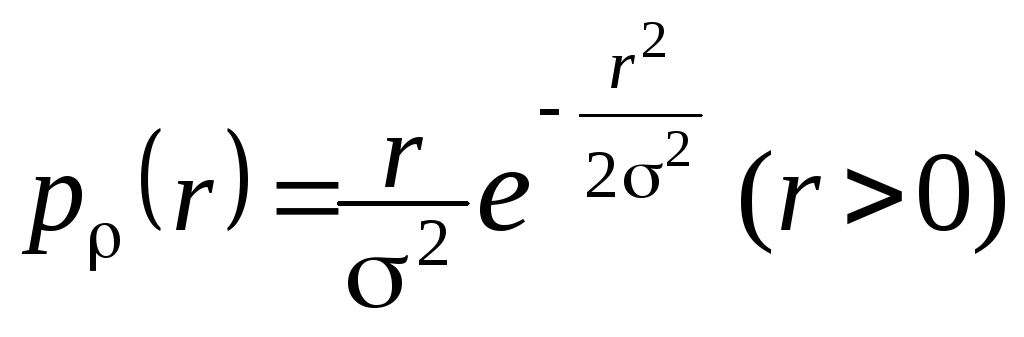. (11)

Розподіл Релея виникає у такій важливій задачі. Розглянемо гармонічні коливання з періодомT :

.

Як відомо з курсу елементарної математики (фізики), такі коливання можна зобразити у вигляді

.

Нехай XтаYнезалежні випадкові величини, розподілені за законом ГаусаN(0;²). Тоді виявляється, що амплітуда та початкова фаза коливаньбудуть незалежними випадковими величинами. При цьому амплітуда буде мати релеєвський розподіл з параметром², а початкова фаза буде рівномірно розподілена у проміжку[0;2).

У тому випадку, коли випадковий вектор розподілений за законом Гауса у найпростішій формі (10) з параметрамиa₁, a₂, ₁²=₂²=², випадкова величина виявляється розподіленою за законом Райса

,

де I₀(x)=. При великих значеннях закон Райса є близьким до нормального .

4) Розподіли ² (Пірсона),  (Стьюдента) та F_n,m (Фішера).Ці розподіли будуть використовуватися у главі 5.

Нехай випадкові величини X₀, X₁,X₂,...,X_nє незалежні та розподілені за законом ГаусаN(0;1). Розподіл випадкової величини_n²=X₁²+X₂²+...+X_n²називається²‑розподілом(хі-квадрат розподілом) зnстепенями свободи. Щільність ймовірності випадкової величини_n² задається співвідношенням (графік щільності приведено на мал.2.24)

,

де стала K_n визначається умовою нормування. Зокрема, випадкова величина₁² =X₁² має щільність ймовірності

.

Цей результат уже приводився в прикладі 3 пункту 2.1.4.

Розподіл випадкової величини називається ‑розподілом (розподілом Стьюдента)зnстепенями свободи. Щільність ймовірності випадкової величини_nзадається співвідношенням (графік щільності приведено на мал.2.25):

,

де стала L_nвизначається умовою нормування.

Графік щільності є симетричним відносно прямої x=0 і подібний до графіка щільності нормального розподілуN(0;1). Із зростанням кількості ступенів свободиnрозподілСтьюдента наближається до нормального з параметрамиa=0,²=1. В таблиці 2 додатка приведені значенняt_(n), які задовольняють рівності

.

Ці значення більші, ніж значення_, що є коренями рівняння 2Ф(_)=1–. Але із зростанням кількості ступенів свободиt_(n) наближається до_. Наприклад, для=0.05 маємоt_0.05(5)=2.5706,t_0.05(10)=2.2281, t_0.05(20)=2.0960, t_0.05(+)=_0.05=1.963 (мал.2.26).

Розглянемо випадкову величину 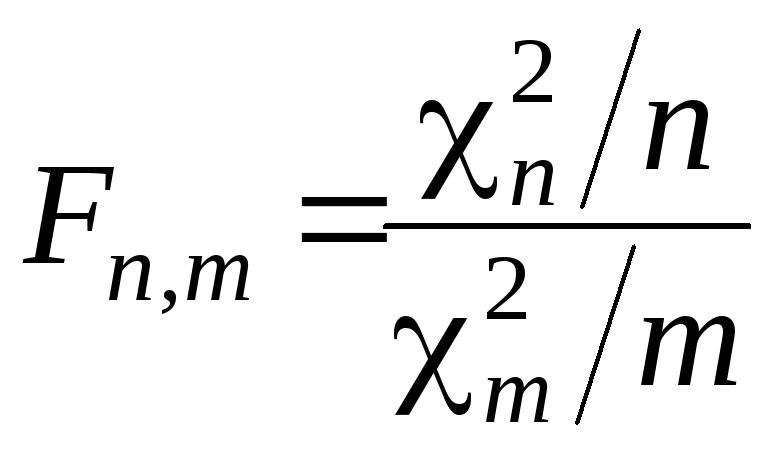, де і – незалежні випадкові величини, розподілені за законом χ² відповідно зn та m ступенями свободи. Розподіл випадкової величиниF_n,mназиваєтьсярозподілом Фішеразn та m ступенями свободи. Щільність цього розподілу має вигляд

,

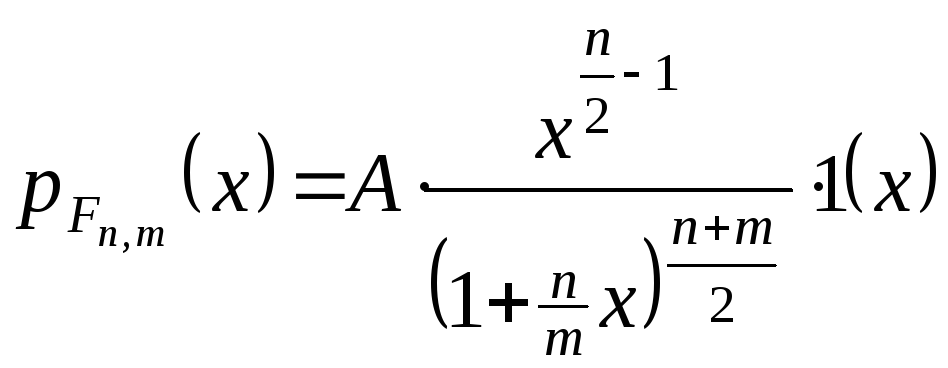де стала Aзнаходиться із умови нормування.