3.3. Кореляція

3.3.1.Коефіцієнт кореляції та кореляційна матриця

Означення 1. Коефіцієнтом кореляції r_X,Y випадкових величин X та Y називається число

. (1)

Коефіцієнт кореляції є безвимірною величиною. Абсолютна величина коефіцієнта кореляції змінюється від нуля (X та Y некорельовані, але можуть бути зв’язаними функціональною залежністю, відмінною від лінійної) до одиниці (X та Y зв’язані лінійно – Y=kX+l): 0|r_X,Y |  1. Якщо r_X,Y >0 (додатна кореляція, прямий зв’язок), то X і Y мають тенденцію зростати і спадати одночасно. Наприклад, додатна кореляція існує між продуктивністю праці та заробітною платою, між зростом людини та її вагою. Якщо r_X,Y  < 0 (від’ємна кореляція, обернений зв’язок), то при зростанні однієї випадкової величини інша має тенденцію спадати і навпаки. Наприклад, від’ємна кореляція спостерігається між продуктивністю праці та вартістю одиниці продукції, між об’ємом продукції та затратами на один виріб.

Наведемо типові діаграми зв’язку між величинами X та Y при різних значеннях r_X,Y (мал.3.4).

Коефіцієнт кореляції є лише мірою лінійної залежності. Чим ближчий коефіцієнт кореляції по модулю до одиниці, тим сильніше залежність X і Y нагадує лінійну і навпаки.

Мірою залежності коефіцієнт кореляції є тільки тоді, коли випадковий вектор розподілений за законом Гауса (формула (9) розділу 2.2). У цьому випадку можна показати, що r_X,Y=r. Тоді рівність r_X,Y =0 означає r=0. Але при r=0 закон (9) розділу 2.2 переходить у закон (10) розділу 2.2, що відповідає незалежності X і Y.

Закон Гауса: некорельованість незалежність

Означення 2. Кореляційною матрицею (матрицею коваріації) випадкового вектора називається симетрична матриця K другого порядку, елементами якої є K_ij=K(X_i,X_j):

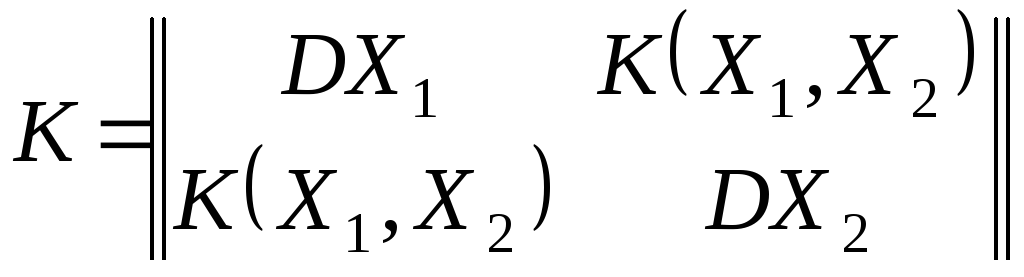. (2)

Можна показати, що вектор математичного сподівання і кореляційна матриця для закону Гауса (формула (9) розділу 2.2) мають вигляд:

.

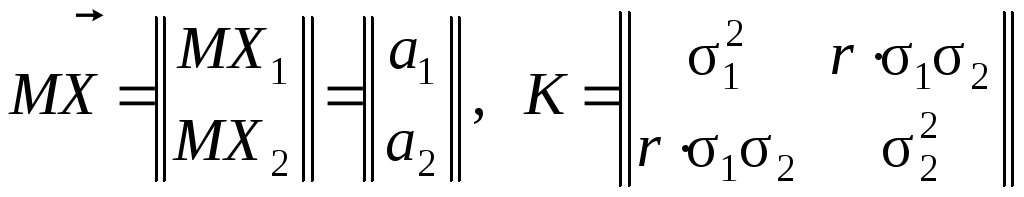Введемо у розгляд вектор . Тоді закон Гауса (9) можна записати у стислому вигляді:

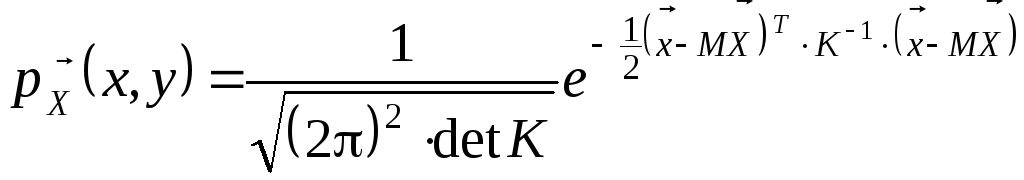, (3)

де T – операція транспонування, K^–1 – матриця, обернена до K, detK - визначник матриці K.

Форма запису (3) справедлива і для n-вимірних нормальних розподілів (X₁; X₂; …; X_n). У цьому випадку

матриця K є симетричною матрицею n-го порядку

.

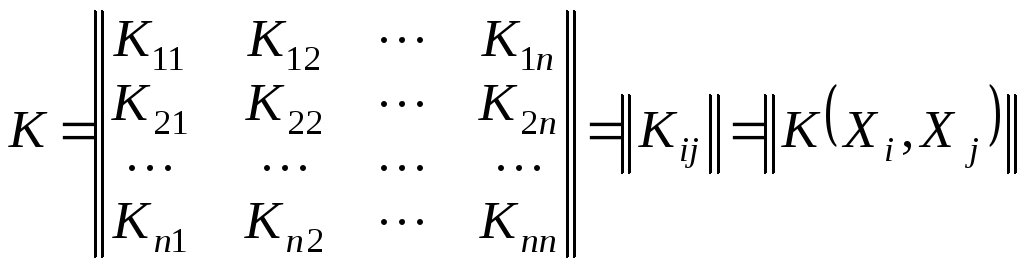Крім того, число (2)² під радикалом у формулі (3) потрібно замінити на (2)ⁿ.

Приклад 1. В умовах прикладу 1 пункту 3.1.5 знайти коефіцієнт кореляції і кореляційну матрицю випадкових величинX і Y.

Розв’язок. Знайдемо дисперсіюX і Y:

.

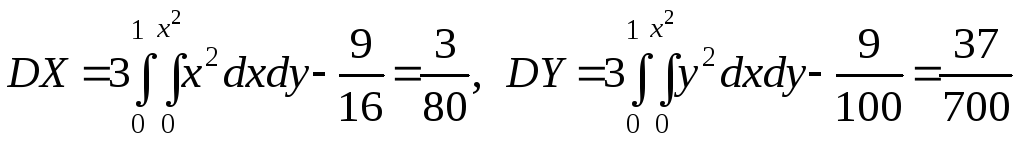Використавши формули (1) та (2), одержимо:

.

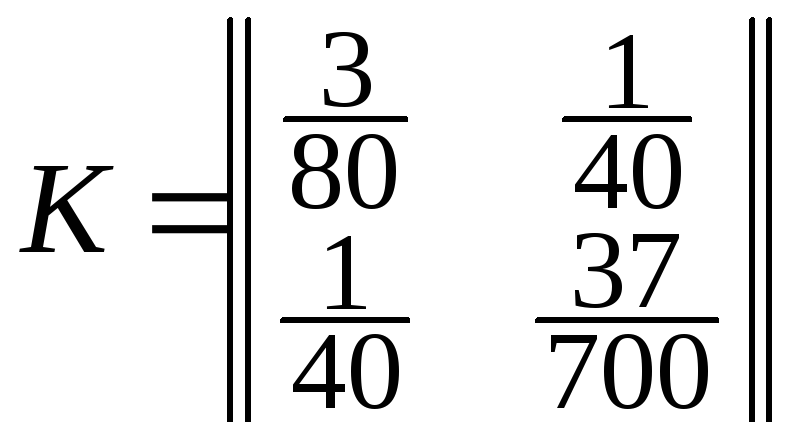Приклад 2. Випадкові величиниX₁, X₂, X₃, X₄, X₅ - попарно некорельовані і мають однакові дисперсії ². Знайти коефіцієнти кореляції випадкових величин: 1)Y₁=X₁+X₂; Y ₂=X₃+X₄+X₅; 2)Y ₃=X₁+X₂+X₃; Y ₄=X₁+X₃+X₅.

Розв’язок.

1)

;

2)

.

Внаслідок формули (5) розділу 3.2 одержимо DY₃=DY₄=3². Отже, на підставі формули (1) .

3.3.2. Регресія

Якщо ми знаємо розподіл однієї координати випадкового вектора при умові, що інша координата приймає певне значення, то можна ввести поняття умовного математичного сподівання.

Означення 1. Умовним математичним сподіванням M(Y/X=x) випадкової величини Y при умові, що випадкова величина X=x, називається число, яке знаходиться за формулою

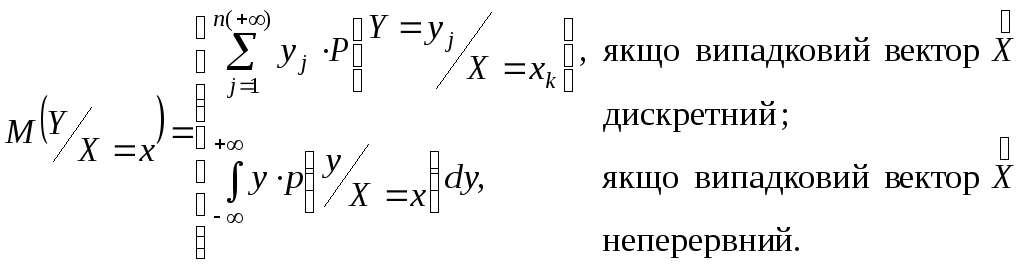(4)

Аналогічно визначається умовне математичне сподівання M(X/Y=y).

При зміні x, взагалі кажучи, змінюється умовне математичне сподівання M(Y/X=x), яке можна розглядати у цьому випадку як функцію x:

M(Y/X=x)=g(x).

Ця функція називається регресією Y на X (Y відносно X), а її графік y=g(x) – лінією регресії Y на X.

Аналогічно визначається регресія X на Y і лінія регресії X на Y:

M(X/Y=y)=h(y), x=h(y).

Випадкові величини X та Y називаються лінійно корельованими, якщо лінії регресії є прямими. Рівняння цих прямих такі:

(5)

Зміст регресії Y на X полягає у тому, що функція g(X) є найкращим наближенням до випадкової величини Y. Це означає, що для довільної функції v(X) виконується співвідношення:

M[Y–v(X)]²  M[Y–g(X)]².

Якщо лінія регресії Y на X(X на Y) не є прямою, можна використати першу (другу) із прямих регресії (5) в якості наближення до істинної лінії регресії. У цьому випадку ця пряма називається прямоюнаближеноїрегресії. У зв’язку з цим відзначимо, що функція (функція ) є найкращим наближенням доY (доX) серед усіх лінійних функцій випадкової величиниX(випадкової величиниY).

Зауважимо, що координати випадкового вектора, розподіленого за законом Гауса (формула (9) розділу 2.2), лінійно корельовані.

Кутові коефіцієнти _Y/Xі_X/Yпрямих регресії (5) називаються відповіднокоефіцієнтами регресіїY на XтаX на Y. При цьому

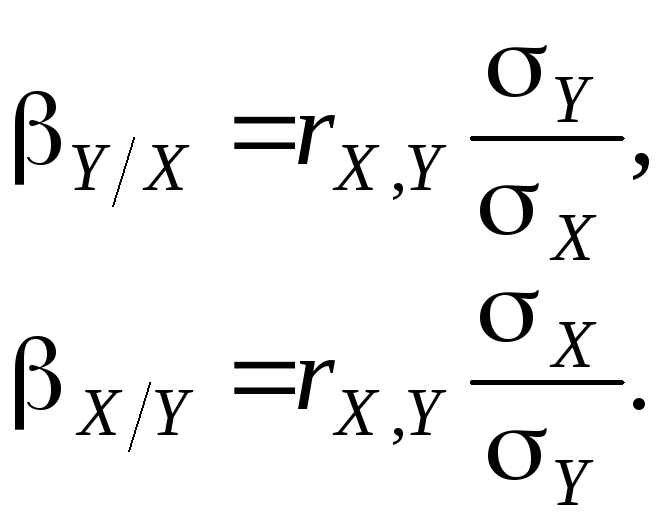(6)

Прямі регресії (5) проходять через точку з координатами (MX; MY). При |r_X,Y |=1 прямі регресії співпадають, а при r_X,Y=0 – паралельні осям координат.

У якості міри розсіювання випадкової величини Yвідносно регресіїg(X) (Y на X) розглядаютькореляційне відношення

. (7)

Із (7) випливають такі властивості кореляційного відношення:

1) ;

2) =1 тоді і тільки тоді, коли між випадковими величинамиX та Y є функціональна залежністьY=g(X);

3) =0 тоді і тільки тоді, колиg(X)=MY, тобто лінія регресії є горизонтальною прямою і, таким чином, випадкові величиниX та Y є некорельованими.

Взагалі кажучи, .

Приклад 1. В умовах прикладу 1 пункту 2.2.3 знайти лінії регресії Y на X та X на Y.

Розв’язок. На підставі (4) (нижній рядок) одержимо:

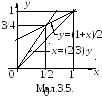
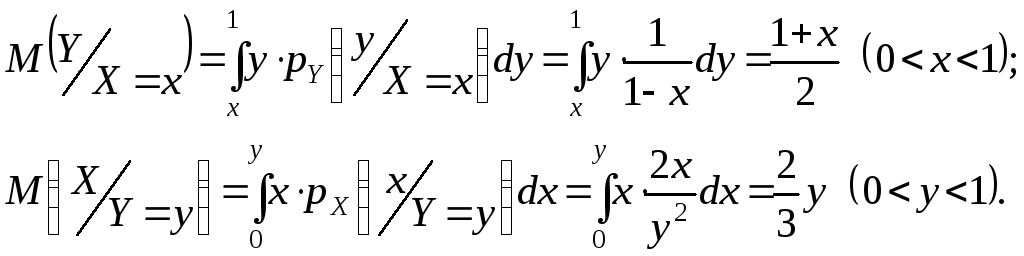
Таким чином, лініями регресії є прямі y=(1+x)/2 (Y на X)і x=(2/3)·y (X на Y) (мал.3.5).

Приклад 2. Випадковий вектор має такі числові характеристики:MX=1, DX=4,MY=2, DY=9, r_X,Y=0.8. У даному випробуванні випадкова величина мала значенняX=1.3. Яке математичне сподівання випадкової величиниY?

Розв’язок. Скористаємося рівнянням прямої наближеної регресіїY на X (5):

.

Підставляючи в це рівняння x=1.3, одержимо y=2.36. Таким чином, M(^Y/_X=1.3)2.36.