3.1.3. Математичне сподівання функції випадкової величини

Теорема 1. Якщо розподіл випадкової величиниXє відомим, то математичне сподівання випадкової величиниY=g(X) дорівнює

(2)

Наслідок.Якщоk іl - є сталими, то

M(kX+l)=k·MX+l. (3)

Зокрема, математичне сподівання сталої дорівнює цій сталій.

Випадкова величина називається центрованою, якщо її математичне сподівання дорівнює нулю. Випадкова величина =X–MXназивається флуктуацією випадкової величиниX. Із (3) випливає, що флуктуація є центрованою випадковою величиною. Дійсно, M=M(X–MX)=MX–MX=0.

Приклад 1. Випадкова величина X задана щільністю p_X (x)=4x³ (x[0;1]). Знайти математичне сподівання випадкових величин: 1) Y=2X ² – X ; 2) Y=.

Розв’язок. На підставі формули (2) знаходимо:

1) M(2X ²–X )=.

2) .

3.1.4. Математичне сподівання функції випадкового вектора

Сформулюємо результат, в якому формули (1) та (2) містяться як окремі випадки.

Теорема 1. Якщо відомий розподіл випадкового вектора , то математичне сподівання випадкової величини Z=g(X,Y) знаходиться за формулою

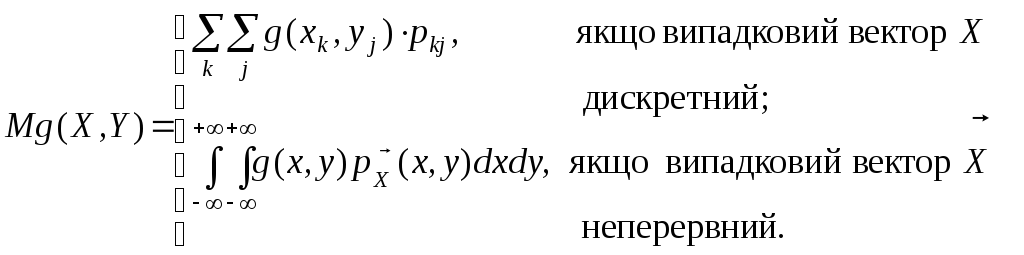(4)

Зокрема, якщо випадкова величина g(X,Y) дорівнюєX, Y, X+Y, X·Yприходимо до формул (формули записані лише для випадку неперервних випадкових величин):

(5)

(6)

. (7)

Із формул (5)–(7) виходять такі властивості математичного сподівання.

Теорема 2. Математичне сподівання суми випадкових величин дорівнює сумі їх математичних сподівань

M(X+Y )=MX+MY.(8)

Доведення. Скористаємося лінійністю інтеграла у формулі (6) а потім формулами (5).

Теорема 3. Математичне сподівання добутку незалежних випадкових величинX таY дорівнює добутку математичних сподівань цих випадкових величин

M(X·Y )=MX·MY.(9)

Доведення.  Оскільки випадкові величини X та Y незалежні, то . У цьому випадку інтеграл у формулі (6) розпадається на добуток інтегралів, один із яких згідно з формулою (1) є MX, а другий – MY.

З

X	–1	1
P	1/2	1/2

ауваження. Із справедливості співвідношення (9) не випливає незалежність випадкових величин X та Y. Дійсно, нехай,Y=X².

Тоді MX=(–1)·1/2+1·1/2=0,

MY=M(X ²)=1·1/2+1·1/2=1,M(X·Y)=M(X ³)=(–1)·1/2+1·1/2=0.

Таким чином, M(X·Y)=MX·MY, але випадкові величиниX таYзалежні не тільки в імовірнісному сенсі, а і функціонально.

Приклад 1. Знайти математичне сподівання випадкової величиниX, яка має біноміальний розподіл (розділ 2.1, формула (4)).

Розв’язок. БудеморозглядатиX, як кількість появ подіїA у серії зnнезалежних випробувань з імовірністюpпояви в кожному з них. Позначимо черезX_i(i=1,...,n) кількість появ подіїAуi-му випробуванні. ТодіX=X₁+X₂+...+X_n і на підставі (8) одержимо: MX=MX₁+MX₂+...+MX_n. Оскільки величини X_i мають однаковий розподіл, то на підставі результату прикладу 1 пункту 3.1.2, одержимо MX=n·MX_n=n·p. Звідси випливає, що математичне сподівання частоти X/n появ події A дорівнює M(X/n)=.

Приклад 2. В теорії масового обслуговування зустрічається випадкова величина, що є сумоюnнезалежних випадкових величин, кожна з яких розподілена за показниковим законом з параметром. Знайти математичне сподівання випадкової величини.

Розв’язок. Враховуючи результат прикладу 3 пункту 3.1.2, на підставі формули (8) будемо матиM=n/.

Закон розподілу величини – закон Ерлангаn–1-го порядку (пункт 2.2.4, наслідок 2).