1.5.2. Асимптотичні формули для схеми Бернуллі.

Формула (1) приводить до громіздких обчислень при великих значеннях n і k, а також при малих значеннях p або 1– p. Тому, доцільно мати наближені, але прості формули для розрахунку відповідних ймовірностей.

1) Формула Пуассона

, (2)

де , справедлива для великихnта малихp (нечасті події).

Приклад 1. Ймовірність виходу мікросхеми із ладу протягом заданого проміжку часу дорівнює 0.003. Яка ймовірність того, що із 200 мікросхем: а) жодна не вийде з ладу; б) вийдуть з ладу не більше двох?

Розв’язок. Точний розв’язок прикладу одержуємо за формулою (1) при n200 і p0.003:

;

Наближений розв’язок знаходимо за формулою (2) при =0.6:

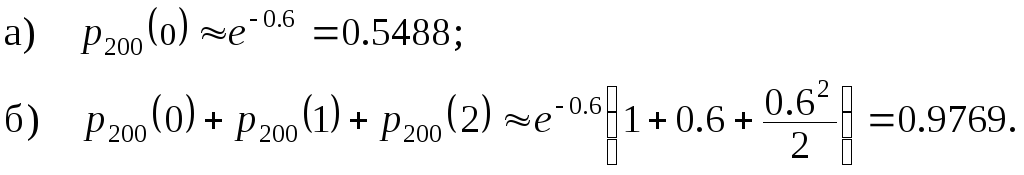
2) Формула Муавра-Лапласа

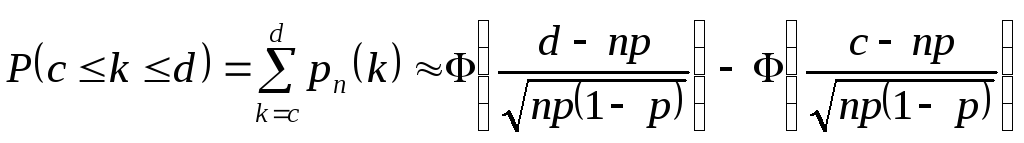(3)

справедлива для великих nтаnp(1– p)10. У таблиці 1 додатка наведені значення, а на малюнку 1.17 графік функції, яка називається функцією Лапласа або інтегралом помилок.

П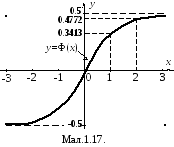риклад 2. Гральний кубик підкидається 1200 раз. Знайти ймовірність того, що кількість випадань одиниці знаходиться в діапазоні між 195 та 210 включно.

Розв’язок. Скористаємося формулою (3) при n1200 і p1/6, c195, d210. Оскільки np200, ,d– np 10, c– np  – 5, шукана ймовірність дорівнюватиме

Приклад 3. Скільки разів потрібно підкинути монету, щоб із ймовірністю не меншою за 0.95 частота появи герба відрізнялась від ймовірності p=0.5 не більше ніж на 0.03.

Розв’язок.

За умовою задачі потрібно знайти n з нерівності . Оскільки, то з формули (3) приnpn/2, dn/2+0.03n, cn/2– 0.03nвиходить співвідношення

.

З таблиць знаходимо, що . Таким чиномn1067.

Формула (3) може бути використана і для оцінки невідомої ймовірності події, якщо відомо скільки разів ця подія зявилась в серії з n випробувань. Нехай ймовірність p появи події А в одному випробуванні невідома. Проводиться серія із n випробувань, у якій подія А зявляється k разів. Потрібно знайти проміжок, який з заданою ймовірністю 1–  накриває невідоме експериментатору значення p. Із формули (3) виходить, що

.

У таблиці функції Лапласа знаходимо те значення _, для якого 2Ф(_)1–  (наприклад, якщо 1– 0.9, 0.95, 0.99, то відповідно _1.6449, 1.96, 2.5758). Потім потрібно розв’язати відносноpнерівність.

Одержаний при цьому проміжок значень дляpприйнято називатидовірчимпроміжком з рівнем надійності 1–  (докладніше про це говориться у розділі 5.3). Наприклад, приn10000, k500, 1– 0.95 для ймовірності pмаємо проміжок

p [0.046;0.055].

2.Випадкові величини

2.1. Одновимірні випадкові величини

2.1.1. Випадкова величина та її функція розподілу

Означення 1.Одновимірноювипадковою величиноюназивається величина, значення якої залежить від наслідку експерименту (інакше кажучи, випадковою величиною називається числова функція, яка визначена на просторі елементарних подій).

У літературі для позначення випадкової величини найчастіше використовуються великі літери X,Y,Zлатинського алфавіту, а для їх можливих значень – відповідні малі літериx,y,z.

Наведемо кілька прикладів випадкових величин: 1) кількість попадань у ціль при п‘яти пострілах; 2) кількість відмов приладу протягом заданого проміжку часу; 3) результат вимірювання фізичної величини; 4) тривалість проміжку часу між двома послідовними відмовами ЕОМ; 5) відстань від центра мішені до точки попадання.

Випадкова величина дає змогу разом з простором  розглянути інший більш простий простір ₁ у якому елементарні події є значеннями випадкової величини (про це, по суті справи, йшла мова в зауваженні до прикладу 5 пункту 1.1.1).

Означення 2.Функцією розподілувипадкової величиниXназивається задана на всій осіOxфункція , яка визначається співвідношенням

F_X (x) = P{X < x} (–∞< x <+∞). (1)

Ф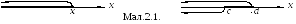ункція розподілу є неспадною функцією, такою, щоF_X (–∞)=0 (ймовірність неможливої події),F_X (+∞)=1 (ймовірність вірогідної події). Знаючи функцію розподілу, можна знайти ймовірність того, що випадкова величина попадає у проміжок[c; d)(мал.2.1):

P{X[c; d)} = P{X < d}–P{X < c} =F_X (d) – F_X (c). (2)