1.5. Повторні випробування

1.5.1. Схема я.Бернуллі. Узагальнення а.Маркова

Багато прикладних задач (наприклад, контроль якості) зводяться до слідуючої схеми.

Розглядається серія із n незалежних випробувань з двома можливими наслідками, в кожному з яких подія A може відбуватись з імовірністю p (випробування незалежні, якщо ймовірність будь-якого наслідку будь-якого випробування не залежить від того, які були наслідки інших випробувань). Нехай A_j (j1,2,...,n) позначає подію, що означає наставання події A у j-му випробуванні. Тоді кожну з 2ⁿ елементарних подій серії можна зобразити у вигляді добутку n множників, кожен з яких дорівнює A_j або .

Теорема. Ймовірністьp_n(k) того, що у серії з n випробовувань подія настає k раз, задається рівністю

. (1)

Доведення. Події, що нас цікавить, сприяють ті елементарні події, у яких події A_j спостерігаються k раз, а події – (n – k) раз (наприклад, ,і т.п.).В силу незалежності подійA_j ймовірність кожної такої елементарної події на підставі теореми множення ймовірностей дорівнює p^k(1– p)^n-k.Оскільки подібних елементарних подій буде, то з урахуванням їх несумісності і теореми додавання ймовірностей остаточно одержимо

.

Приклад 1. Точки та тире телеграфного коду спотворюються незалежно одне від іншого з ймовірністю 0.12. Знайти ймовірність події, яка полягає у тому, що в слові з п’яти символів буде спотворено: а) два символи; б) не більше одного символу.

Розв’язок. Задача зводиться до схеми Бернуллі при n=5 і p=0.12.

а) k=2 і на підставі формули (1) маємо

·0.12²·0.88³= 0.098;

б) k0 або k1 і тому ймовірність дорівнює

P₅(0)+ P₅(1)= 0.88⁵+ 5·0.12·0.88⁴=0.5377+ 0.3598= 0.888.

Приклад 2. На кожному з двох крил літака установлені по два двигуни, кожен з яких може вийти з ладу під час польоту незалежно один від одного з імовірністю p0.1. Яка ймовірність того, що політ закінчиться нормально, якщо: а) літак може летіти на будь-яких двох двигунах; б) літак може летіти при умові, що на кожному крилі працює хоча б один двигун.

Розв’язок. Позначимо через A подію, яка полягає у тому, що політ закінчиться нормально.

а) Нехай D_k – подія, яка полягає у тому, що під час польоту вийдуть із ладу лише k (k= 0,1,2,3,4) двигуни. Тоді , де подіїD₃ і D₄ несумісні. Таким чином, . При обчисленніP(D₃) і P(D₄) скористаємося схемою Бернуллі при n=4 і p=0.1:

P(D₃)= p₄(3)= ·p³ ·(1– p)= 4·(0.1)³·0.9= 0.0036;

P(D₄)= p₄(4)= ·p⁴ ·(1– p)⁰=4·(0.1)⁴=0.0001.

Тому P(A)=1–P()=1– 0.0036– 0.0001=0.996.

б) Нехай П_k (Л_k) – подія, яка полягає у тому, що під час польоту на правому (лівому) крилі вийдуть із ладу лише k (k= 0,1,2) двигуни.

Тоді подію A можна представити у вигляді суми несумісних подій: A=П₁·Л₀+П₀·Л₁+П₁·Л₁+П₀·Л₀. При обчисленні P(П₀)=P(Л₀) і P(П₁)=P(Л₁) скористаємося схемою Бернуллі при n=2 і p=0.1:

P(П₀)=p₂(0)=·p⁰ ·(1– p)²=(0.9)²=0.81;

P(П₁)=p₂(1)=·p·(1– p)=2·0.1·0.9=0.18.

Таким чином, з урахуванням незалежності подій П_k і Л_j одержимо:

P(A)=P(П₁)·P(Л₀)+P(П₀)·P(Л₁)+P(П₁)·P(Л₁)+P(П₀)·P(Л₀)=

 = 0.18·0.81+0.81·0.18+0.18·0.18+0.81·0.81= 0.98.

Важливим узагальненням схеми Бернуллі є схема однорідного ланцюга А.Маркова. У цьому випадку припускаємо, що ймовірність будь-якого наслідку у j-му випробуванню залежить лише від наслідку попереднього (j-1)-го випробування, але не залежить ні від j (номера випробування) ні від наслідків випробувань з номерами j–2, j–3,...,1. Введемо позначення:

,,,.

Я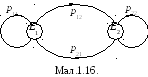кщо подіямAта поставити у відповідність станиE₁ та E₂ деякої системи, то граф переходу цієї системи з одного стану в інший матиме вигляд, показаний на малюнку 1.16. Вершинами графа є стани системи, а стрілка з числомp_ik,що йде з вершиниE_iу вершинуE_k,означає, що умовна ймовірність переходу із стануE_i у станE_k дорівнюєp_ik.У цьому випадку числаp_ik називаються ймовірностями переходу зі стану E_i у стан E_k, а матриця – матрицею перехідних ймовірностей. (У випадку послідовності незалежних випробувань матриця перехідних ймовірностей має вигляд).

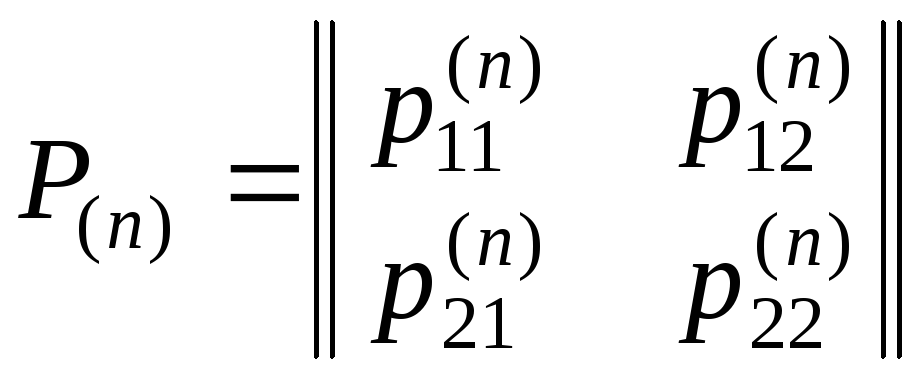Позначимо через ймовірність переходу зі стануE_i у стан E_k за n випробувань, а через –матрицю переходу за n випробувань. Із формули повної ймовірності випливає співвідношення

.

Можна показати, що якщо всі елементи p_ikматриці перехідних ймовірностейPдодатні, то приn → ∞існують і не залежать від початкового стануE_iграниці ймовірностей переходу:

.