
- •СОДЕРЖАНИЕ
- •2. АНАЛИТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
- •2.1. Математические модели.
- •2.2. Типовые схемы моделирования
- •2.3. Непрерывно-детерминированные модели (D-схемы)
- •2.6. Марковский случайный процесс
- •Рис. 2.4. Система АЛУ – память
- •2.7 Непрерывно – стохастические модели (Q – схемы)
- •2.7.1. Системы массового обслуживания. Потоки событий
- •2.7.2. Простейший поток
- •2.7.3. Непрерывные марковские цепи. Уравнения Колмогорова
- •2.7.4.Диаграмма интенсивностей переходов
- •2.7.5 Формула Литтла
- •2.7.7. Замкнутые системы массового обслуживания (СМО с ожиданием ответа)
- •2.7.8. Распределение Эрланга. Метод этапов
- •Рис 2.20. Пример использования метода псевдосостояний
- •2.7.8. Немарковские СМО
- •3. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ
- •3.1. Условия применения имитационного моделирования
- •3.2. Этапы имитационного моделирования
- •3.3. Способы моделирования случайных величин
- •3.4. Равномерно-распределённые случайные числа (РРСЧ).
- •3.4.1. Методы формирования РРСЧ.
- •3.4.2. Проверка качества последовательностей РРСЧ
- •3.5. Формирование случайных величин с заданным законом распределения.
- •3.5.1. Метод обратной функции.
- •3.5.2. Универсальный метод
- •3.5.3. Метод исключения (отбраковки, режекции, Дж. Неймана)
- •3.5.4. Метод композиции (суперпозиции).
- •3.6. Формирование случайных векторов с заданными вероятностными характеристиками
- •3.7. Моделирование случайных событий
- •3. 8. Сетевые модели
- •3.8.1. Сети Петри
- •3.8.2. Е-сети
- •3.8.3. Сетевая модель взаимодействующих параллельных процессов в операционной системе.
- •3.9. Управление модельным временем
- •3.10. Планирование машинных экспериментов
- •3.11. Обработка экспериментальных данных
- •3.11.1. Экспериментальные оценки
- •3.11.2. Оценки для математического ожидания и дисперсии
- •3.11.2. Доверительные интервал и вероятность
- •3.11.3. Точность. Определение числа реализаций
- •ЛИТЕРАТУРА
- •Основная литература
Тогда пункт 2 будет иметь вид: |
xj = a+(b-a)max ((η1, η2) . |
3.5.4. Метод композиции (суперпозиции).
Этот метод может быть применён, когда применение метода обратной |
|
|||||
функции |
или |
метода |
исключения |
становится |
затруднительным |
вви |
сложности функции . |
|
|
|
|
||
Суть |
метода |
заключается в разбиении фигуры, образуемой графиком, |
|
|||
функции fξ(x) на произвольное число непересекающихся областей, форма которых позволяет использовать один из ранее рассмотренных методо
формирования случайных величин (рис. 3.13). |
|
функцииfξ(x) |
||
Другими |
словами, осуществляется |
апроксимация |
||
композицией более простых функций в виде |
|
|
||
|
¥ |
¥ |
|
|
|
fx (x) = åPjj j (x) , где |
å Pj |
=1. |
|
|
j =1 |
j =1 |
|
|
Значение Pj фактически представляет собой площадь фигуры qj.
При практической реализации метода число компонент в композиции конечно:
N
fx (x) = å Pjj j (x) .
j =1
Здесь φj(x) – условные плотности вероятностей, соответствующие форме qj. Их ординаты получаются делением Pj на(нормированием) отрезков вертикальных прямых, лежащих в области qj.
Имитация реализацийξ сводится в этом случае к реализации дискретной величины j, распределение которой задано рядом вероятностей
P1, P2, … , PN,
т.е. к выбору одной изφj и к имитации величины с плотностьюφj(x) одним из известных способов.
Основной принцип разбиения заключается в том, что частям qi, имеющим наибольшую площадь (т.е. наибольшее значение Pi) должны соответствовать наиболее просто и быстро имитируемые плотности φi(x).
100
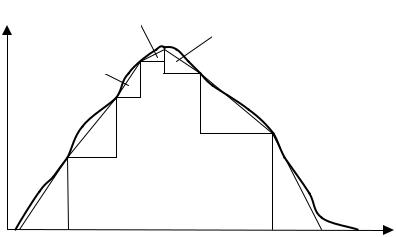
fξ(x) |
q5 |
q6 |
|
q4 |
|
||
|
|
||
|
|
|
|
|
q3 |
q7 |
|
|
|
|
|
|
|
q1 |
|
q2 |
|
q8 |
x |
|
|
|
Рис. 3.13. Метод композиции Например, разбиению на рис. соответствуют:
–ступенчатая плотность φ1 (хорошо применим универсальный метод);
–треугольные плотности φ2 – φ7 (наиболее удобен метод исключений);
–остаточная плотность:
|
7 |
|
|
|
f ( x ) - å Pij i |
|
|
j 8 = |
i = |
1 |
. |
7 |
|
||
1 - å Pi
i =1
Таким образом, моделирующий алгоритм включает следующие этапы:
––разбиение области под графиком fξ(x) на N непересекающихся областей qj достаточно простой формы и определение их площадей ;
––для каждой qj строится условная плотностьφj(x), ординаты которой получаются делением на Pj отрезков вертикальных прямых x=const, лежащих в области qj;
|
|
|
|
|
k |
|
|
–– |
строится шкала 0, a1, a2, ..., aN=1, где |
ak = åPi ; |
|
|
|||
|
|
|
|
|
i =1 |
|
|
–– |
генерируется равномерно распределенное число η из диапазона от 0 до |
|
|||||
1 и с его помощью определяется номер k плотности φk(x) по условию: |
|
|
|||||
–– |
с |
ak-1< η< ak; |
из |
рассмотренных |
ранее |
методо |
|
использованием |
одного |
||||||
формируется случайное числоxi |
с функцией плотности распределенияφk(x), |
|
|||||
которое включается в выходную последовательность. |
|
|
|||||
Если чисел нужно больше, то последние два пункта |
повторяются |
||||||
необходимое число раз. |
|
|
|
|
|
||
101
