3.5. Формирование случайных величин с заданным законом распределения.

Для формирования чисел с заданным законом распределения исходным

относительно Fξ(x) функции (рис. 3.6.б): xi= Fx-1 ( yi).

Докажем, что случайная величина, значения которой получены в соответствии с (3.1), будет иметь равномерное распределение.

Пусть η – равномерно распределена от 0 до 1. Рассмотрим случайное число x = j(h) , где функция φ – монотонна и непрерывна.

91

Рис. 3.6. Метод обратной функции

Тогда h = j -1(x) .

Найдем функцию распределения для величины ξ :

Fx (x) = P(x < x) = P(j(h) < x) .

интервале (0, 1) распределения и равна 1 в этом интервале и 0 вне его. Окончательно получим:

Fx (x) = j -1(x) .

Отсюда:

j(h) = F -1(h) = x . x

Таким образом, функция φ, связывающая равномерно распределённую величину η с величиной ξ, имеющую функцию распределения Fξ есть функция

F -1, т.е. обратная по отношению к Fξ. x

Рассмотрим пример использования метода обратной функции.

Надо получить число с показательным законам распределения. Для него функция плотности имеет вид:

f x (x) = le-lx .

Получим функцию распределения для показательного закона:

92

В соответствии с тем, что было рассмотрено выше, если в это выражение подставить величину xi, имеющую показательное распределение, то в результате получится число yi, равномерно распределенное от 0 до 1:

Если величина yi равномерно распределена от0 до 1, то и 1- yi будет обладать этим же свойством, поэтому окончательно:

1

хi = - l ln( yi ) .

Итак, если в нашем распоряжении имеются числа{yi}, равномерно распределенные от 0 до 1, то, воспользовавшись полученным выражением, можно вычислить последовательность чисел{хi}, имеющих показательное законам распределение.

3.5.2. Универсальный метод

Для использования метода обратной функции необходимо иметь в явном виде аналитическое выражение для функции распределения вероятностейFξ(x). Как правило, законы распределения задаются функцией плотностиfξ(x) а функцию распределения получают интегрируя fξ(x):

x

Fx (x) = ò fx (x)dx .

-¥

Для многих распределений использование метода обратной функции в аналитическом виде оказывается затруднительным или невозможным по ряду причин:

а) интеграл от fξ(x) не берётся, либо после интегрирования получается выражение, требующее больших затрат машинного времени;

б) описание вида распределения получено экспериментально в виде гистограммы.

В этих случаях используют универсальный способ получения случайных чисел, основанный на кусочной аппроксимации функции плотности.

93

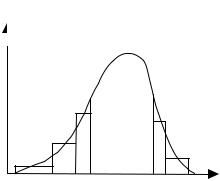
Пусть требуется получить последовательность случайных чисел{хi} с функцией плотности распределения fξ(x).

Если область определения случайной величиныξ не ограничена, перейдём к усеченному распределению на интервале (c,d). Разобъём интервал (c,d) на n подинтервалов (рис. 3.7)

(a0, a1), (a1, a2), ... , (an-1, an), a0=c, an=d.

Границы интервалов выбираются так, чтобы вероятность попадания в любой из подинтервалов(ak, ak+1) была постоянной, то есть не зависела отk. Для вычисления границы ak воспользуемся следующим соотношением:

fξ(x)

Рис. 3.7. Кусочная аппроксимация функции плотности

В простейшем случае будем представлять fξ(x) в виде кусочно-постоянной функции, то есть считаем значение fξ(x) на xкаждом подинтервале постоянной. Тогда значение случайной величины , ξпопадающей в подинтервал(ak, ak+1) можно представить как

xk = ak + ηk*,

где:

выходной последовательности

xk = ak + (ak+1- ak) η2.

94

границами a0, a1, a2, ... , an-1, an.

Р

Рис. 3.8. Задание закона распределения гистограммой

Построим вспомогательную шкалу: 0, с1, с2, с3,…, сn, 1,

аналитическом виде. Для этого предварительно рассчитывают значения Рi как

ai

Pi = ò f (x)dx

ai-1

95