происходящий в системе, марковским не является, и для него мы не можем написать алгебраические уравнения.

S21 — ремонт начинается; S22 — ремонт продолжается; S23 — ремонт заканчивается,

т. е. разделим ремонт на три этапа, причем время пребывания системы в каждой

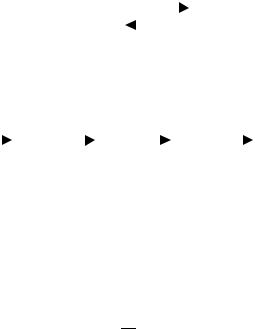
Рис 2.20. Пример использования метода псевдосостояний

Запишем уравнение для предельной вероятности состояния P1:

λP1=μP23,

m

P1 = l P23 .

Нормировочное уравнение:

65

Заметим, что метод псевдосостояний допускает сравнительно простое решение задачи только в самых простых случаях, когда число состояний исходной системы невелико. Однако, иногда удается применить этот метод и к задачам, где число состояний не очень мало; во всяком случае, получить если не буквенное, то численное приближенное решение соответствующей системы линейных алгебраических уравнений. Рассмотрим в связи с этим

процедуру построения модели с неограниченной очередью аппроксимации потока обслуживания или входного потока потоком Эрланга.

1. Система М/Еk/1. Входной поток − простейший с интенсивностьюλ,

поток обслуживания − поток Эрланга порядкаk с интенсивностью L = m ( μ − k

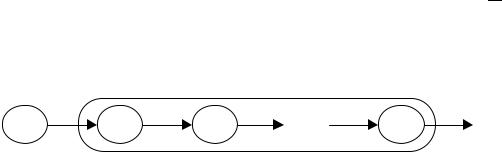
интенсивность порождающего простейшего потока). Очередь не ограничена. Структура этой системы представлена на рис. 2.21.

Будем описывать состояние системы в определённый момент времени общим числом этапов обслуживания, через которое должны пройти все находящиеся в этот момент в системе заявки до полного завершения их обслуживания.

Если в системеn заявок, а обслуживаемая находится наi-ом этапе обслуживания, то общее число этапов обслуживания для всех заявок, то есть текущее состояние:

j = (n -1)k + (k - i + 1) = nk - i +1.

ДИП для этой системы представлена на рис. 2.22.

66

Используя закон сохранения потоков вероятностей (сумма входящих равна сумме исходящих), построим систему алгебраических уравнений для предельных вероятностей состояний:

стационарности lm <1, предельные вероятности состояний существуют и могут быть найдены.

Рис 2.22. ДИП для системы М/Еk/1/∞

Для этого можно использовать следующий прием. Переходим к системе М/М/1/∞ с интенсивностью потока обслуживанийμ. Задаваясь определенной точностью, находим максимальное количество заявок, которые могут реально находиться в системе. Тем самым мы ограничиваем ДИП и систему уравнений

для системы М/Е/1/∞. Теперь эту систему можно решить и найти вероятности

r

состояний Pi. Для дальнейшего анализа характеристик эффективности системы

При большом числе состояний удобно использовать для решения системы

67

интенсивностью kλ. Структура этой системы представлена на рис. 2.23.

Рис 2.23. Система Еr / М /1/∞

Будем описывать состояние системы в определённый момент времени общим числом этапов поступления, через которые прошли все находящиеся в данный момент в системе заявки плюс количество этапов, пройденных вновь поступающей заявкой.

Если в системеn заявок, а очередная поступающая находится наi-ом этапе, то общее число этапов поступления для всех заявок, то есть текущее состояние:

j = nk + i -1.

На вход приёмного устройства поступает новая , заявкакак только предыдущая появляется на его выходе. Уход из системы обслуженной заявки уменьшает суммарное число этапов поступления на k.

ДИП для этой системы представлена на рис. 2.24.

68