или
P |
= |
an - a0 |
× |
f (ai ) + f (ai +1) |
, |
|
|
||||
i |
|
n |
2 |
|
|
|
|
|
|||
а далее по описанному выше алгоритму.
3.5.3. Метод исключения (отбраковки, режекции, Дж. Неймана)
Основой метода является следующая теорема:
Если множество точек(x,y) является реализацией случайного вектора 
x,h
, равномерно распределенного в области, ограниченной осью 0X и кривой
f(x), такой, что
¥
ò f (x)dx = G < ¥ ,
-¥
то одномерная плотность распределения величины ξ равна jx (x) = f (x) G .
Отсюда следует, что, если f(x) – искомая функция плотности распределения (т.е. G =1), то, реализовав процедуру построения множества случайных векторов, равномерно распределенных под графикомf(x), мы, тем самым, получим множество значений абсцисс{xi}, распределённых в соответствии с законом, определяемым функцией f(x).
Однако, процедура генерирования случайных векторов может оказаться достаточно сложной в вычислительном плане(надо использовать условные функции плотности ввероятностей). Для упрощения процедуры формирования
случайных |
чисел |
|
воспользуемся |
следующим |
достаточно |
очевид |
||||||
утверждением. |
|
|
|
|
|
|
|
|
равномерно распределён под кривой g1(x) , такой, что |
|
||
Если вектор |
|
|
|
x,h |
|
|
|
|
||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
g1(x) ³ f (x) ³ 0 |
|
|
|
для всей области определенияf(x), то его реализации, ограниченные областью между 0X и f(x) будут равномерно распределены в этой области.
Функция g1(x) называется мажорирующей функцией по отношению кf(x)
(рис. 3.9) .
y
f(x)
g1(x)
G1
G
96 |
x |
Рис. 3.9. Мажорирующая функция
Можно выбрать функциюg1(x) такой, что вектора, равномерно распределенные в областиG1 , будет просто генирировать. Удобно выбирать функцию, имеющую постоянное значение на всей области определения f(x):
g1(x)= const,
как правило, равное максимальному значению fmax функции f(x).
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fmax |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(xi) |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yi |
|
|
|
|
x |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
а |
xi |
b |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Рис. 3.10. Метод исключения |
|
|
|
|
|
|
|
|||||||
Отсюда вытекает процедура метода (рис. 3.10): |
|
|
|
|
|
|
|
||||||||||
а) |
если функция f(x) не |
ограничена, то, учитывая |
допустимую |
||||||||||||||
погрешность, область ее определения ограничивают интервалом (a,b); |
|||||||||||||||||
)б |
имитируется |
|
реализация (xi,yi) вектора |
|
|
|
x,h |
|
|
|
, |
равномерно |
|||||
|
|
|
|
||||||||||||||
распределеного в области G1 (между OX и g1(x)): |
|
|
|
|
|
|
|
||||||||||
–генерируется РРСЧ xi из диапазона (a,b);
–генерируется РРСЧ yi из диапазона (0, fmax(x));
в) если, yi<f(xi) то (xi,yi) является реализацией вектора, распределённого в области G (между осью 0X и f(x)) и xi – искомая реализация ξ. Иначе процедура повторяется, начиная с пункта б).
Так как в качестве базовой последовательности обычно берут ,числа равномерно распределенные в диапазоне от 0 до 1, то от случайной величины ξ сискомой функцией распределения f ξ переходят к случайной величине
ξ* = x - a . b - a
Для нее область возможных значений(0, 1), а функция плотности вероятностей имеет вид
fξ*(z) = (b-a)f ξ[a+(b-a)z]
(сжатие по оси абсцисс).
97
Произведем сжатие по оси ординат: f*ξ*(z) = fξ*(z)/fmax ,
где fmax максимальное значение fξ*(z).
В результате произведенных действий функцияf*ξ*(z) расположилась в единичном квадрате в начале системы координат.
Теперь процедура получения последовательности чисел с функцией плотности fξ(x) сводится к следующему.
1)генерируется пара РРСЧ из диапазона (0, 1) – ηi, ηi+1;
2)проверяется выполнение условия
3) |
|
|
ηi+1 £ f*ξ*( ηi ) ; |
|
|
|
|
|
|
||||||
если это условие выполняется, то очередное число, включаемое в |
|||||||||||||||
выходную последовательность получаем как |
|
|
|
|
|
||||||||||
|
|
|
xj = a+(b-a) ηi , |
|
|
|
|
|
|
||||||
иначе процедура повторяется, начиная с пункта 1. |
|
|
|
|
|
||||||||||
Эффективность |
метода |
|
|
исключения |
характеризуется |
коэффициентом |
|||||||||
использования kn – отношением количества отобранных реализаций к общему |
|||||||||||||||
числу |
реализаций. |
Очевидно, |
|
что |
|
это |
отношение |
при |
|
равномерном |
|||||
распределении |
реализаций |
|
равно |
отношению |
площадей |
под |
графиками |
||||||||
функций f(x) и g1(x): |
|
|
G |
|
|
|
|
|
|
|
|
|
|||
|
|
|
kn |
= |
£ 1, |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
¥ |
|
¥ |
|
G1 |
|
|
|
|
|
|
|
|
||
где G1 = ò g1(x)dx , а G = ò f (x)dx . |
|
|
|
|
|
|
|
|
|
|
|||||
|
-¥ |
|
-¥ |
|
|
|
|
|
|
|
|
|
|
|
|
Чем ближе значениеkn |
к 1, |
тем |
эффективнее |
использование |
метода. |
||||||||||
Можно, |
например, |
использовать |
|
|
в |
качестве мажорирующей |
функцииg1(x) |
||||||||
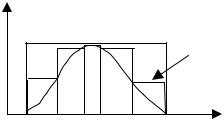
ступеньчатую функцию (рис. |
). |
При |
этом |
значение |
коэффициентаkn |
||||||||||
увеличивается, |
но |
следует иметь в ,видучто при этом одновременно |
|||||||||||||
увеличивается число вычислений. |
|
|
|
|
|
|
|
|
|
|
|||||
g1(x) |
. . . . |
Рис. 3.11. Ступенчатая мажорирующая функция
Пример. 3.1.
Рассмотрим использование метода для получения чисел с треугольным распределением:
98
|
|
ì2(x - a) |
x Î[a, b]; |
|
||||||||||
|
|
ï |
|
|
|
|
|
|
||||||
|
|
|
- a) |
2 |
|
|
|
|||||||
|
|
fx (x) = í(b |
|
|
|
|
|
|
|
|
|
|||
|
|
ï |
|
|
|
|
|
x Ï[a, b]. |
|
|||||
|
|
î0 |
|
|
|
|
|
|||||||
Переходим от случайной величиныξ к величине ξ*, реализацией которой |
||||||||||||||
является значение |
x - a |
|
|
|
|
|
|
|
||||||
|
|
z = |
. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
b - a |
|
|
|
|
|
|
||||
Значениz z |
лежат в |
диапазоне от0 до 1 (рис. б) |
и для нее функция |
|||||||||||
плотности распределения |
|
|
|
|
|
|
2( a + ( b - a )z - a ) |
|
|
|||||
fξ*(z) = (b-a)f ξ[a+(b-a)z]=( b - a ) |
|
= 2z . |
||||||||||||
( b - a )2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
а) |
|
|
|
|
|
|
|
fξ(x) |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
0 |
|
a |
|
|
|
|
b |
|
||||||
fξ*(z)
б) |
1 |
|
f*ξ*(z) |
|
|
|
|||
|
|
|
||
|
|
|
|
z |
|
0 |
1 |
|
|
Рис. 3.12. Имитация треугольного распределения Максимальное значение эта функция принимает при z=1:
fmax=2. |
|
Произведем масштабирование по вертикальной оси: |
|
f*ξ*(z) = fξ*(z)/fmax =z. |
единичный квадрат |
Таким образом, мы пришли к функции, вписанной в |
|
(рис. 3.12. б). |
|
Теперь формирование чисел с треугольным |
распределением будем |
производить по следующему алгоритму: |
|
1)Берём η1 и η2 − равномерно распределенные в диапазоне от0 до 1 числа;
2)Если η1 > η2, то включаем в выходную последовательность очередное число xj = a+(b-a) η1 , иначе переходим к пункту 1.
Для ускорения процедуры можно заполнять квадрат сразу парами точек, симметричными относительно диагонали с координатами (η1, η2) и (η2, η1) .
99