В

качестве а берут число близкое

к2n2 , x0 – любое

нечётное число

меньше

М, а значение С подбирают

экспериментально,

оно влияет на

корреляционные свойства последовательности.

Эффективность

статистического

моделирования

систем

на

ЭВМ

достоверность

получаемых

результатов существенным

образом

зависят

от

качества исходных (базовых)

последовательностей псевдослучайных

чисел,

которые являются основой для получения стохастических воздействий

на

элементы

моделируемой

системы. Поэтому, прежде

чем

приступать

к

реализации моделирующих алгоритмов на ЭВМ, необходимо убедиться в том,

что

исходная

последовательность

псевдослучайных

чисел

удовлетворяет

наличии

абсолютно

правильного

алгоритма

моделирования

проце

функционирования моделируемой

системы по результатам моделирования

нельзя

будет достоверно

судить

о

характеристиках

системы. Поэтому

все

системы

пройти

тщательное

предварительное

тестирование, которое

представляет

собой

комплекс

проверок

по

различным

статистически

критериям, включая в качестве основных проверки(тесты) на равномерность,

стохастичность и независимость. Кроме того,

очень важными показателями

качества базовой последовательности являются длина периода и длина отрезка

апериодичности. Рассмотрим возможные методы проведения таких проверок,

наиболее часто используемые в практике статистического моделирования.

1) Проверка равномерности.

Проверка

равномерностипоследовательностей

псевдослучайных

квазиравномерно распределенных чисел{хг} может быть выполнена по

гистограмме или с использованием косвенных признаков.

а) Проверка по гистограмме (рис.3.4).

Суть проверки по гистограмме сводится к следующему. Выдвигается

гипотеза о

равномерности распределения чиел в

интервале(0 1).

Затем

интервал

(0 1)

разбивается на m

равных частей. При генерации

последовательности РРСЧ подсчитывается количество попаданийNk в каждый

из m

подинтервалов. Вычисляется

относительная

частота

попадания

случайных чисел последовательности {хг} в каждый из подинтервалов

0

1

x22i -1 + x22i <1.

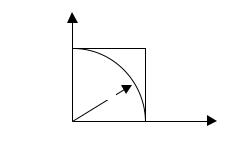
Геометрически это означает, что точка с координатами(x2i-1,

x2i)

расположена внутри четверти круга радиусаR=1, вписанного в единичный

квадрат (рис. 3.5).

случае точка(x2i-1, x2i) всегда

В

общем

попадет

внутрь

единичного

квадрата. Тогда теоретическая вероятность попадания этой точки в четверть

круга равна отношению площади четверти круга

к

площади

единичного

квадрата:

P = S1/4 круга/Sквадрата = (πR2/4)/(1·1) = π/4.

Если

числа

последовательности{хг} равномерны,

то

в

силу

закона

больших чисел теории вероятностей при большихN относительная частота

попадания

точки

в единичный квадрат, равная

отношению числаK пар (x2i-1,

x2i), для

которых проверочное условие выполнелось к общему числуN/2

пар

1

R

0

1

x2i-1

2) Проверка стохастичности

чисел{хг}

Это

исследование

последовательностей

псевдослучайных

наиболее часто проводится методами комбинаций и серий.

а) метод комбинаций

Сущность

метода

комбинаций

сводится

к

определению

зако

распределения закона распределения(появления) числа единиц (нулей) в n-

разрядном двоичном числехг. На практике длину последовательностиN

берут достаточно большой и проверяют всеп разрядов или только l старших

разрядов числа хг .

Теоретически закон появления j единиц в l разрядах двоичного числа

описывается

исходя из

независимости

отдельных

разрядов биномиальным

P( j,l) = C j P j (1)[1 - P(1)]l - j

= C j Pl (1),

l

l

где P(j,l) − вероятность появления j единиц в l разрядах числа хг; P(1)=P(0)=0,5

− вероятность

появления единицы

(нуля)

в любом

разряде

числахг;

Clj = l!/[ j!(l - j)!] .

Тогда при

фиксированной длине выборкиN теоретически ожидаемое

число появления случайных чисел jс единицами в проверяемыхl разрядах

будет равно

= NClj Pl (1) .

n j

После

нахождения

теоретических

и

экспериментал

ìa ,

если

xi < p;

xi = í

если

xi ³ p,

îb

Так как

случайные числа

и b в данной последовательности

независимы

и принадлежат

последовательности {хг}, равномерно

здесь понимается генерация числаxi

и проверка условия xi<p) определится

формулой Бернулли

P( j,l) = c j p j

(1 - p)l - j ,

j =

l =

.

0,l,

1, n

l

3) Проверка независимости

Случайные

величины ξ и η

называются

независимыми,

если

закон

распределения каждой из них не зависит от того, какое значение приняла

другая.

Проверка

независимости

проводится

на

основе

выч

корреляционного

момента.В

общем

случае

корреляционный

моме

случайных величин ξ и η

с возможными значениямиxi и

yj определяется по

формуле

Kxh = åå(xi - M [x ])( yi - M [h])Pij

i

j

где Рij – вероятность того, что (ξ, η) принимает значение (xi, yj), а М[ξ], М[η] –

математические ожидания случайных величин.

Если случайные числа независимы, то Kξη = 0.

Независимость элементов последовательности {хг} может быть проверена

путем введения

в

рассмотрение последовательности{yr} такой, что

{yr} =

{хг+τ}, где τ – величина сдвига последовательностей.

удобней

использоват

Иногда

вместо

корреляционного

момента

коэфициент корреляции

Kxh

r xh

=

,

s x s h

rxh

£ b

1

.

N

1

N -t

1

N -t N -t

(

å xi xi +t -

å xi å xi +t )

(N

-t )2

r xh

=

N -t i =1

i =1 i =1

,

где

D[xi ]D[xi +t ]

1

N -t

1

N -t

D[x

] = [

] å

(x2

-

( å x )2 ) ,

i

(N -t )

i=1

i

(N -t )2

i

i=1

1

N -t

(x2

1

N -t

)2 ) .

D[x

i +t

] =

å

-

( å x

i

+t

N -t

i =1

i +t

(N - t)2

i =1

не имеет

места. Это означает,

что

все числаxi в

пределах отрезка

апериодичности не повторяются.

Очевидно, что

использование

при

моделировании

систем - после

довательности

чисел {хг}, длина которой

больше отрезка апериодичностиL,

может привести к повторению испытаний в тех же условиях, что и раньше, т.

е. увеличение числа реализаций не дает новых статистических результатов.

Способ

экспериментального

определения

длины

периодаР и

длины

начальным

значением x0

на V

значений, фиксируется xv (обычно

полагаютV = (1 ¸ 5)106 );

1)

Использование рекуррентных формул порядка r

xi +1 = Ф(xi , xi-1, ... , xi -r +1) .

Естественно, это ведёт

к увеличению затрат машинного времени на

получение чисел и ограничивает возможности его применения на практике.

2)

Метод возмущений

ìФ(xi ), если

i mod M ¹ 0,

xi +1 = í

i mod M = 0,

îy (xi ), если

Vi= ai, i=1 ¸k.

случайный

Затем с помощью числа от второго датчика разыгрывается

выбор номера s элемента в массиве V:

s=[bjk], где скобки означают «целая часть».

пересылается

в

Выбранный

элемент

массива

последовательности {ai}:

Этот

cj= Vs, Vs= ak+j ( j=1,2, ...).

ослабить

зависимость

между

ч

метод

позволяет

последовательности {ci}

и получить

чрезвычайно

большие периоды, если

периоды последовательностей {ai} и {bi} − взаимно простые числа.