4. Уравнения токов

Повторим еще раз уравнения (2.8):

;

Согласно методу симметричных составляющих

или ;

или ,

где , – эффективные числа витков фаз и.

Разделив левую и правую части последних выражений на w_эB, получим

; , (4.1)

где – уже известный коэффициент трансформации двигателя.

Подставляя (4.1) в выражение и решая систему двух уравнений относительно , получим

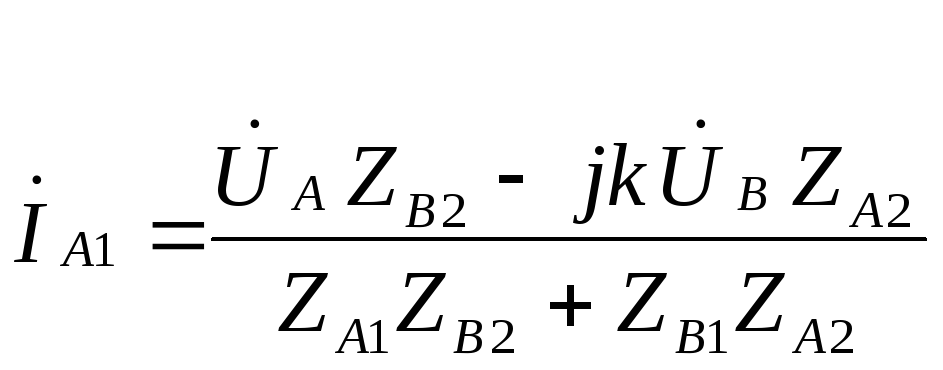, . (4.2)

Рассчитав и , легко определитьи, а затем найти полные токи фази.

4.1. Электромагнитная мощность. Вращающий момент несимметричного двухфазного микродвигателя

Поскольку в рассматриваемых микродвигателях имеют место поля токов прямой и обратной последовательностей, электромагнитная мощность – мощность, передаваемая от статора к ротору магнитным полем, должна быть равна сумме мощностей этих последовательностей.

Как известно, при круговом поле электромагнитная мощность равна потерям в активном сопротивлении ротора, деленным на скольжение для прямого и надля обратного полей

, (4.3)

Если выразить токи и сопротивления фазы через токи и сопротивления фазы

; ;, (4.4)

подставить в (4.3), ( ), то после преобразований получим

. (4.5)

Выражение (4.5) неудобно для практических расчетов тем, что в него входят токи ротора. Это обстоятельство можно обойти, если воспользоваться схемами замещения рис. 3.1. Действительно, в параллельном соединении: “контур намагничивания – цепь ротора” (рис. 3.1), существует только одно активное сопротивление . В преобразованных схемах замещения рис. 3.2 в состав,тоже входит активное сопротивление , .Поэтому в соответствии с законом сохранения энергии потери мощности в этих сопротивлениях должны быть одинаковыми, т.е.

;.

С учетом этого выражение электромагнитной мощности приобретает простой вид

. (4.6)

Если разделить электромагнитную мощность на синхронную угловую частоту вращения, получим выражение вращающего момента

. (4.7)

При этом перед электромагнитной мощностью обратной последовательности следует поставить знак "минус", ибо обратное поле создает не движущий, а тормозной момент.

На рис. 4.1 представлена механическая характеристика асинхронного двигателя при эллиптическом поле, как результат действия прямого и обратного полей, создающих вращающий и тормозноймоменты.

Рис. 4.1. Механическая характеристика двухфазного асинхронного двигателя

с эллиптическим магнитным полем

Из рис. 4.1 видно негативное действие обратного поля:

• снижение максимального и пускового моментов,

• увеличение номинального скольжения и, как следствие, увеличение потерь в роторе, снижение КПД машины.

Задача 4.1. Определить пусковой момент несимметричного двухфазного двигателя, параметры схемы замещения которого

; ;;;;;;.