4. Ранг матриці та способи його обчислення

Нехай ми маємо прямокутну матрицю А розміром .

Рангом матриці А називається найбільший з порядків її мінорів, відмінних від нуля.

Так, наприклад, ранг матриці дорівнює нулю, а матрицідорівнює двом.

Якщо в матриці А є відмінний від нуля мінор порядку , а всі мінори-го порядку або дорівнюють нулю, або не існують, то.

При обчисленні рангу матриці можна користуватися елементарними перетвореннями (вони не змінюють ранг матриці): множенням деякого ряду матриці на число, відмінне від нуля; додаванням до одного ряду матриці другого, паралельного йому ряду, помноженого на деяке число; перестановкою місцями двох паралельних рядів матриці.

Відмінний від нуля мінор матриці, порядок якого дорівнює рангу матриці, називається базисним мінором матриці.

Якщо в матриці деякий ряд можна представити у вигляді суми інших паралельних йому рядів, помножених відповідно на числа , то даний ряд називаютьлінійною комбінацією вказаних рядів. Декілька паралельних рядів матриці називаються лінійно-залежними, якщо хоча б один з них є лінійною комбінацією інших. В противному випадку паралельні ряди називаються лінійно-незалежними.

Має місце така теорема (про базисний мінор).

Будь-яка стрічка (стовпчик) матриці є лінійною комбінацією базисних стрічок (стовпчиків). Базисні стрічки (стовпчики) матриці лінійно незалежні.

Отже, ранг матриці дорівнює максимальному числу лінійно незалежних паралельних її рядів.

При обчисленні рангу матриці можна користуватися методом зведення матриці до трапецієвидної форми, методом обвідних мінорів та ін.

Метод зведення до трапецієвидної форми полягає в тому, що за допомогою елементарних перетворень матриця зводиться до вигляду

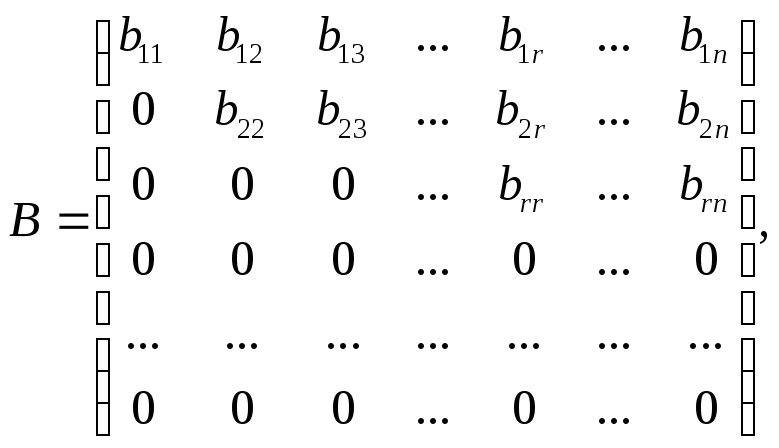
де відмінні від нуля. При цьому(і дорівнює рангові вихідної матриці).

Мінор порядку , який містить в собі мінорпорядку, називаєтьсяобвідним мінором для .

Метод обвідних мінорів оснований на тому, що ранг матриці дорівнює порядку такого мінору цієї матриці, який відмінний від нуля, а всі обвідні його мінори дорівнюють нулю.

5. Теорема Кронекера-Капеллі

Розглянемо лінійну систему рівнянь зневідомими

(1)

де – дійсні числа. Матрицяназиваєтьсяматрицею системи, а матриця –розширеною матрицею системи.

Систему (1) можна записати в матричній формі , деа також у вигляді

(2)

Має місце теорема Кронекера-Капеллі.

Система (1) сумісна тоді і тільки тоді, коли ранг розширеної матриці дорівнює рангові матриці А:.

Дійсно, якщо система (1) сумісна, то з (2) випливає, що системи стовпчиків А і еквівалентні, і.

Якщо ж , то останній стовпчик (2) лінійно виражається через інші і, отже, система (1) сумісна. Теорему доведено.

Правило розв’язання системи (1).

Нехай система (1) сумісна, причому . Вибираємо в_{А r} лінійно незалежних рядків та залишаємо в (1) лише ті рівняння, коефіцієнти яких увійшли у вибрані рядки.

В цих рівняннях зліва залишаємо такі невідомих, що визначник із коефіцієнтів при них відмінний від нуля. Інші невідомі оголошуємо вільними і переносимо їх в праві частини рівнянь. Розв’язуємо систему, виражаючи базисні невідомі (зліва) через вільні невідомі (справа).

Зауважимо, що однорідна система завжди сумісна, бо має тривіальний (нульовий) розв'язок. Якщо однорідна система має безліч розв’язків, то із всієї їх сукупності виділяють так звану фундаментальну систему – будь-яку максимальну лінійно незалежну систему розв’язків. При цьому якщо ранг матриці дорівнює, то фундаментальна система розв’язків складається зрозв’язків. Щоб одержати розв’язки фундаментальної системи, вибирають довільний відмінний від нуля визначник-го порядку і кожен його рядок приймають за значення вільних невідомих. Якщо цей визначник відповідає одиничній матриці, то одержуютьнормовану фундаментальну систему розв’язків.

Наприклад. Знайти нормовану фундаментальну систему розв’язків системи

. Знайдемо ранг матриці системи:

; обвідні мінори дорівнюють нулю.

Отже, . За базисний мінор можна взятиТоді базисними невідомими будутьта. Запишемо систему у вигляді

.

Знайдемо

Тоді

Отже, множина розв’язків системи має вигляд:

.

Поклавши тут спочатку а потім –одержимо нормовану фундаментальну систему розв’язків:

, ,