Семінарське заняття 2

Тема 2. Системи лінійних алгебраїчних рівнянь

Питання для усного опитування та дискусії

2.1. Формули Крамера.

2.2. Метод Гаусса.

2.3. Матричний метод розв’язування систем рівнянь.

2.4. Ранг матриці.

2.5. Теорема Кронекера - Капеллі.

Аудиторна письмова робота

Виконання студентами тестових завдань з питань теми заняття.

Методичні вказівки

Ключовими термінами, на розумінні яких базується засвоєння навчального матеріалу теми, є : формули Крамера, прямий хід метода Гаусса, зворотний хід метода Гауса, матричний метод, ранг матриці, метод обвідних мінорів, зведення матриці до трапецієвидної форми, теорема Крон екера – Капеллі, сумісність (несумісність) системи рівнянь.

З метою глибокого засвоєння навчального матеріалу при самостійному вивченні теми студенту варто особливу увагу зосередити на таких аспектах.

1. Метод Крамера

Розглянемо систему трьох лінійних рівнянь

_.

Розв’язком системи (1) називається будь-яка трійка чисел , яка задовольняє систему.

Введемо до розгляду визначник системи , а також визначники_{Dx, Dy, Dz} за формулами:

Якщо , то система (1) має єдиний розв'язок, що визначаєтьсяформулами Крамера:

(2)

(якщо , то система (1) або несумісна, або має безліч розв’язків).

Аналогічні формули мають місце для системи рівнянь зневідомими.

Наприклад. Розв’язати методом Крамера систему рівнянь

Розв'язування. Обчислимо головний визначник системи :

.

Оскільки , можна користуватись формулами Крамера (2). Знайдемота:

Отже, згідно з формулами Крамера (2), маємо:

Відповідь:

2. Метод Гаусса

Існують і інші методи розв’язування систем рівнянь. Покажемо, як розв’язують систему лінійних рівнянь зневідомими (п>2) методом Гаусса. (К. Гаусс, 1777 – 1855 – великий німецький математик ).

Проілюструємо метод Гаусса на прикладі, який ми розв’язали раніше методом Крамера (тут ). Перше рівняння системи є зведеним. Проілюструємо прямий хід метода Гаусса за допомогою перетворення таблиці коефіцієнтів вихідної системи:

Здійснюючи обернений хід, одержуємо:

(отже, );

(отже, ).

Обидві відповіді співпали.

Зауважимо, що з останньої таблиці можна одержати аналогічним способом дві такі таблиці:

звідки відразу ж одержується розв'язок системи

Система рівнянь може мати безліч розв’язків.

Наприклад. Розв’язати методом Гаусса систему рівнянь

_.

Розв'язування.

Звідси одержуємо:

Відповідь: – множина розв’язків системи.

Система рівнянь може бути несумісною. Наприклад, система

несумісна, оскільки в результаті прямого ходу метода Гаусса одержуємо:

.

3. Розв’язування систем матричним методом

За допомогою матриць система трьох лінійних неоднорідних рівнянь з трьома невідомими запишеться так:

або (1)

(тут А – матриця виду 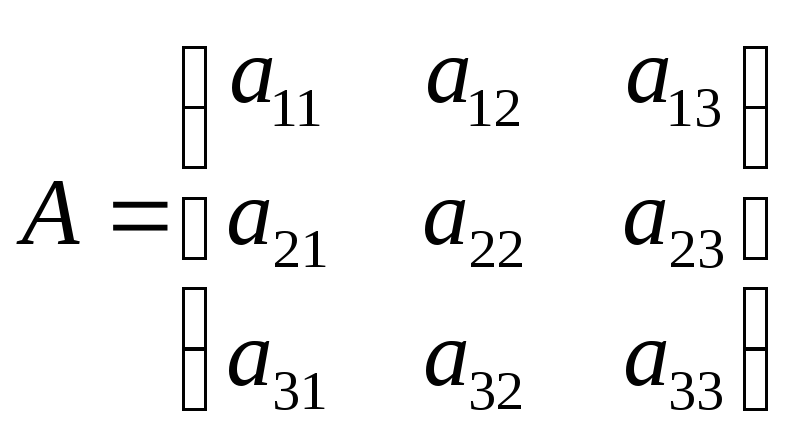,– вектор виду,– вектор виду). Припустимо, що.

Домножимо обидві частини рівняння (1) зліва на :

.

Оскільки, одержуємо:

(2)

Формула (2) – результат розв’язання системи матричним способом. Для ілюстрації викладеного розв’яжемо систему, розв’язану раніше методом Крамера і методом Гаусса, матричним методом. Отже, маємо:

.

Нагадаємо, що . Обчислимо, щоб визначити обернену матрицю:

;

Маємо обернену матрицю :

.

Визначимо . Отже,, і.

Зауважимо, що метод оберненої матриці (матричний метод) особливо зручний, коли потрібно розв’язати декілька систем рівнянь з однаковими лівими частинами та різними стовпчиками вільних членів – такі системи мають однакову обернену матрицю.