Семінарське заняття 7

Тема 8. Основні теореми диференціального числення функції однієї змінної

Питання для усного опитування та дискусії

8.1. Теореми Ферма, Ролля, Лагранжа, Коші.

8.2. Правила Лопіталя.

8.3. Асимптоти графіка функції.

8.4. Дослідження функції однієї змінної на монотонність, екстремум і на напрямок вигнутості.

8.5. Загальна схема побудови графіка функції.

Аудиторна письмова робота

Виконання студентами тестових завдань з питань теми заняття.

Методичні вказівки

Ключовими термінами, на розумінні яких базується засвоєння навчального матеріалу теми, є : теорема Ферма, теорема Ролля, теорема Лагранжа, теорема Коші, перше правило Лопіталя, друге правило Лопіталя, вертикальна асимптота, похила асимптота, монотонне зростання, монотонне спадання, екстремум (мінімум, максимум), вгнутість, увігнутість, точка перегину.

З метою глибокого засвоєння навчального матеріалу при самостійному вивченні теми студенту варто особливу увагу зосередити на таких аспектах.

1. Теореми Ферма, Ролля, Лагранжа, Коші

Диференціальне числення застосовують для дослідження функцій. Наведемо теореми Ферма, Ролля, Лагранжа, Коші.

Теорема Ферма. Нехай функція , неперервна в деякому інтервалі, приймає своє найбільше (або найменше) значення у внутрішній точціцього інтервалу:. Якщо в точціпохідна функціїіснує, то вона обов’язково дорівнює нулю:.

Теорема Ролля. Якщо функція неперервна в замкненому інтервалі, диференційована у всіх його внутрішніх точках та приймає на кінцях інтервалу рівні значення, то в цьому інтервалі існує хоча б одне значення, для якого.

Теорема Лагранжа. Якщо функція неперервна в замкненому інтерваліі диференційовна у всіх його внутрішніх точках, то в цьому інтервалі існує хоча б одне значення, для якого

.

Ця теорема виражає той факт, що приріст функції на інтервалі дорівнює добуткові похідної в деякій проміжній точці інтервалу на приріст незалежної змінної.

Геометрично теорема Лагранжа означає, що при виконанні умов цієї теореми на лінії АВ завжди знайдеться точка, в якій дотична до лінії буде паралельна хорді, що стягує цю лінію.

Теорема Лагранжа має велике теоретичне значення. Її узагальненням є теорема Коші, за допомогою якої доводиться правило Лопіталя розкриття невизначеностей при знаходженні границь.

Теорема Коші. Якщо функції інеперервні в замкненому інтерваліта диференційовні у всіх його внутрішніх точках, причомуу цих точках не перетворюється в нуль, то в цьому інтервалі існує хоча б одне значення, для якого

.

2. Правило Лопіталя

Наведемо правило Лопіталля граничного переходу, яким зручно користуватися при дослідженні функцій.

Правило Лопіталя. Нехай функції тапри(або) сумісно прямують до нуля або до нескінченності. Якщо відношення їх похідних має границю скінченну чи ні, то і відношення самих функцій також має границю, яка дорівнює границі відношення похідних:

.

Наприклад, .

Деколи цим правилом доводиться користуватися декілька разів. Наприклад:

.

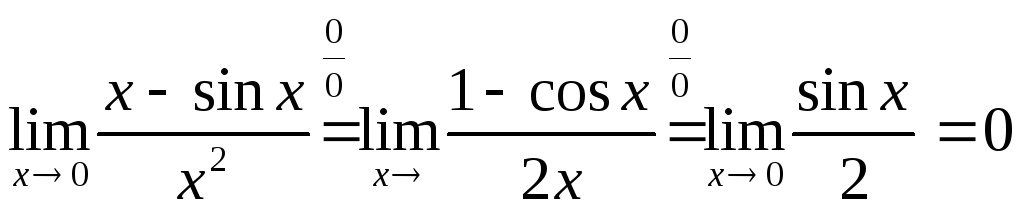Зауважимо, що коли умови, сформульовані у правилі Лопіталя, не виконуються, то границя може існувати чи ні . Так, наприклад, (що легко знайти безпосередньо, без правила Лопіталя). А спроба застосувати правило Лопіталя виявиться невдалою, оскількине існує.

За допомогою правила Лопіталя можна розкривати невизначеності типу ,.

Якщо, наприклад, , апри, то добутокможна представити як частку видуабо. При цьому одержуються невизначеності видуабо, які можна досліджувати за правилом Лопіталя.

Наприклад,

Невизначеності виду, розкривають за допомогою попереднього логарифмування функцій.

Наприклад, це невизначеність типу. Знайдемо, де. Маємо:

.

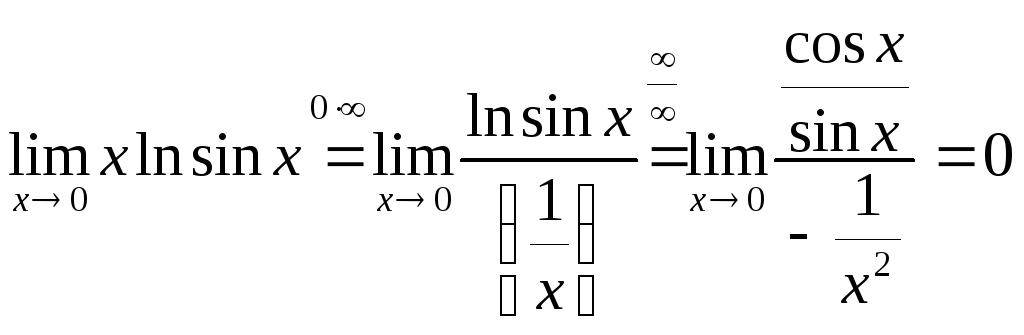Оскільки при, то. Отже,.

Невизначеність типу розкривають за допомогою перетворення різниці в добуток чи частку функцій та подальшим використанням правила Лопіталя.

Наприклад,