
- •Методичні рекомендації
- •1. Опис навчальної дисципліни
- •2. Структура навчальної дисципліни
- •3. Зміст семінарських занять
- •1. Вектори (основні поняття)
- •2. Лінійні операції з векторами
- •Із означення випливає, що (комутативність).
- •3. Лінійна залежність векторів
- •4. Скалярний добуток векторів
- •Визначники другого порядку
- •Визначники третього порядку
- •Основні властивості визначників
- •Матриці та дії з ними
- •Семінарське заняття 2
- •2. Метод Гаусса
- •3. Розв’язування систем матричним методом
- •4. Ранг матриці та способи його обчислення
- •5. Теорема Кронекера-Капеллі
- •Семінарське заняття 3
- •Тема 3. Пряма, площина. Тема 4. Криві та поверхні другого порядку
- •Виконання студентами тестових завдань з питань теми заняття. Методичні вказівки
- •Пряма, площина
- •1. Різні види рівнянь прямої лінії
- •2. Нормальне рівняння площини
- •3. Загальне рівняння площини
- •4. Рівняння площини у відрізках на осях
- •5. Рівняння площини, яка проходить через дану точку; через дані три точки.
- •6. Кут між двома площинами
- •7. Віддаль від точки до площини
- •8. Пряма лінія у просторі (векторне рівняння; параметричні та канонічні рівняння; пряма як лінія перетину площин)
- •9. Кут між прямими
- •10. Кут між прямою і площиною
- •11. Перетин прямої з площиною
- •Лінії другого порядку
- •Поняття про полярну систему координат
- •Поверхні та їх класифікація
- •2. Поверхні обертання
- •3. Поверхні другого порядку
- •Семінарське заняття 4
- •2. Функція двох змінних
- •3. Нескінченно малі та нескінченно великі величини
- •4. Границя послідовності
- •5. Границя функції
- •Семінарське заняття 5
- •Тема 6. Неперервність функції. Точки розриву
- •Виконання студентами тестових завдань з питань теми заняття. Методичні вказівки
- •Семінарське заняття 6
- •Тема 7. Похідна. Диференціал
- •Виконання студентами тестових завдань з питань теми заняття. Методичні вказівки
- •Похідна, її фізичний, геометричний та економічний зміст
- •2. Диференційовність та неперервність функцій
- •6. Диференціал та його геометричне значення
- •7. Похідні та диференціали вищих порядків
- •8. Формула Тейлора
- •9. Частинні похідні та диференціали функції двох змінних
- •10. Похідна по напряму. Градієнт функції
- •Похідною функції в напрямку (де – точка, що лежить на промені ) називається , деі– значення функції в точкахі. Якщо функція– диференційовна, то має місце формула:
- •Наприклад. Знайти похідну функції в точців напрямку, що утворює з віссюкут в. Розв’язок. Визначимо частинні похідні іта обчислимо їх значення в точці:. Враховуючи, що,
- •11. Диференціювання складних функцій
- •12. Геометричні застосування диференціального числення функції двох змінних
- •13. Похідні і диференціали вищих порядків
- •Семінарське заняття 7
- •2. Правило Лопіталя
- •3. Монотонність функції
- •4.Дослідження на екстремум
- •5. Вигнуті та увігнуті криві
- •6. Вертикальні та похилі асимптоти
- •7. Застосування похідної в економіці
- •Семінарське заняття 8
- •Умовний екстремум
- •3. Метод найменших квадратів
- •Таблиця 1
Визначники другого порядку
Визначником (детермінантом) другого порядку називається вираз
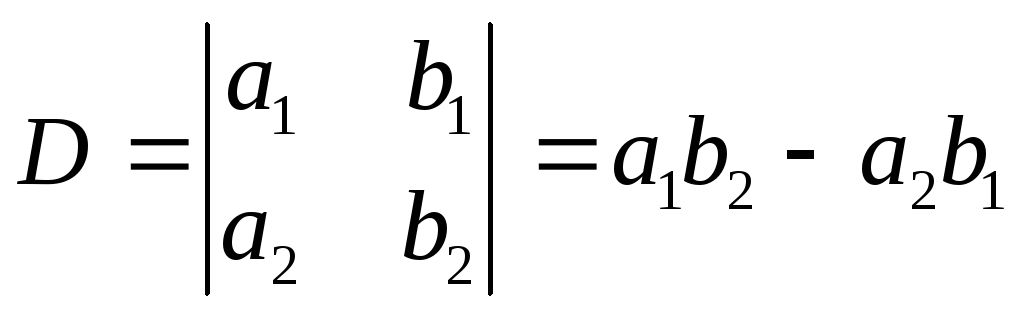 .
(1)
.
(1)
Числа
![]() називаютьсяелементами
визначника. Згідно з формулою (1), маємо
правило обчислення визначника другого
порядку: цей визначник дорівнює різниці
добутків його елементів головної та
другої діагоналі.
називаютьсяелементами
визначника. Згідно з формулою (1), маємо
правило обчислення визначника другого
порядку: цей визначник дорівнює різниці
добутків його елементів головної та
другої діагоналі.
За допомогою визначників зручно розв’язувати лінійну систему двох рівнянь з двома невідомими:
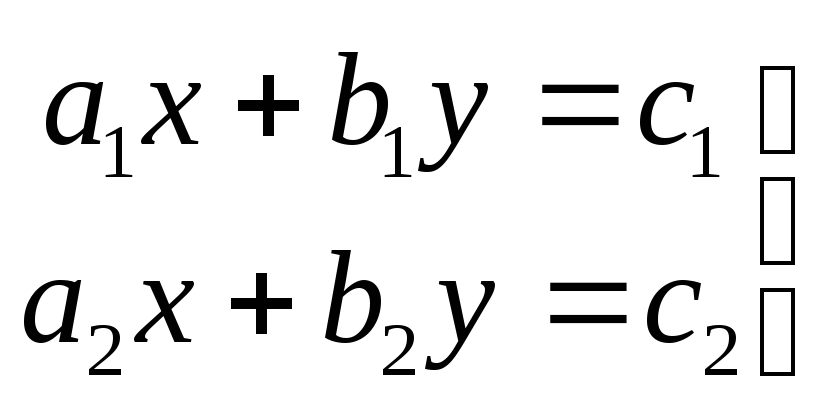 .
(2)
.
(2)
Нагадаємо,
що розв’язком системи (2) називається
будь-яка пара чисел
![]() ,
яка перетворює цю систему в тотожність.
,
яка перетворює цю систему в тотожність.
Розв'яжемо систему (2), виключаючи з неї спочатку одну невідому, а потім – іншу.
Домножимо
перше рівняння системи (2) на
![]() ,
друге – на
,
друге – на![]() і почленно додамо.
і почленно додамо.
У результаті отримаємо:
![]() .
(3)
.
(3)
Аналогічно
можна домножити перше рівняння системи
на
![]() ,
а друге на
,
а друге на![]() ,
почленно їх скласти. Маємо:
,
почленно їх скласти. Маємо:
![]() .
(4)
.
(4)
Введемо такі визначники:
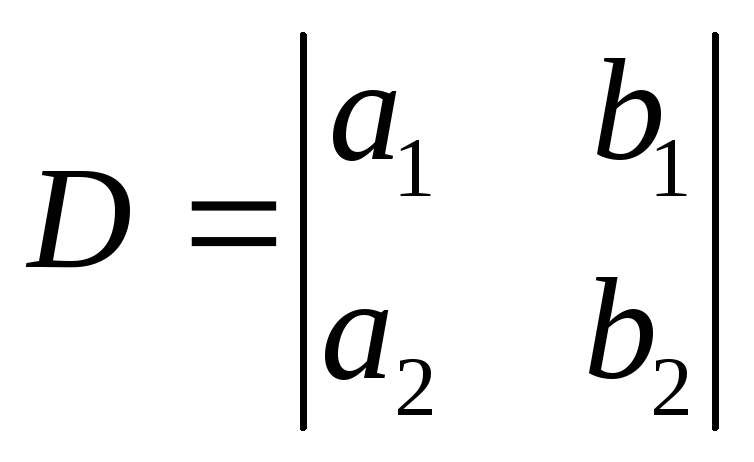 –головний
визначник системи, а також додаткові
визначники
–головний
визначник системи, а також додаткові
визначники
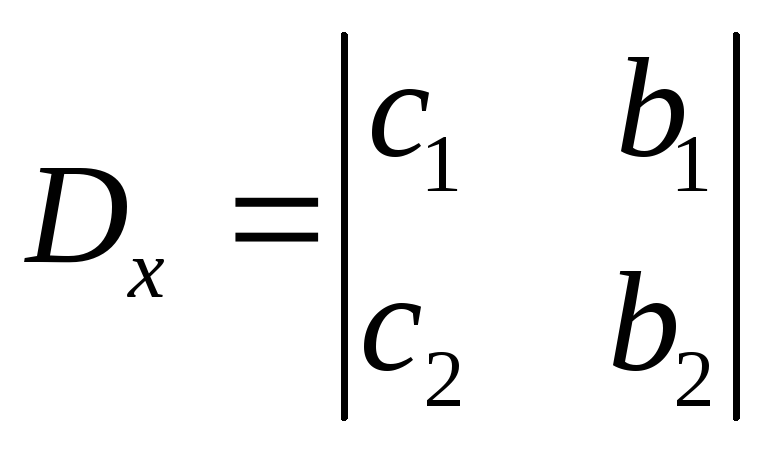 та
та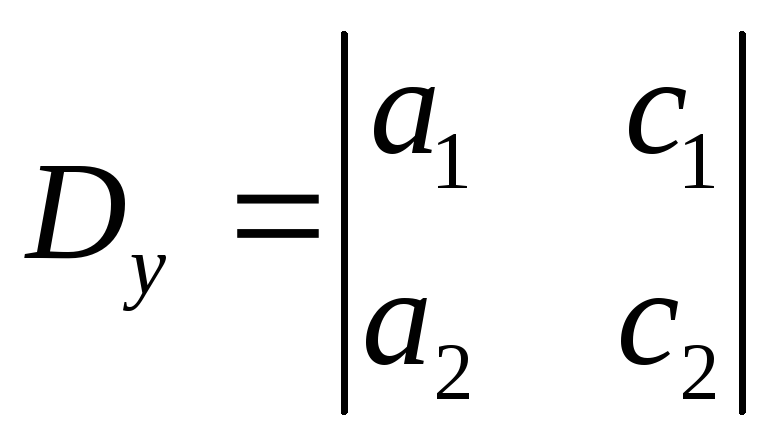 .
.
Завдяки цим позначенням рівняння (3) і (4) можна представити у вигляді
![]() ,
,
![]() (5)
(5)
Якщо
![]() ,
то з формул (5) одержуємо
,
то з формул (5) одержуємо
![]() (6)
(6)
Це –
формули Крамера. Вони дають розв'язок
системи рівнянь (2) при
![]() (якщо
(якщо![]() ,
то система (2) або несумісна, тобто не
має розв’язків, або невизначена, тобто
має нескінченно багато розв’язків).
,
то система (2) або несумісна, тобто не
має розв’язків, або невизначена, тобто
має нескінченно багато розв’язків).
Наприклад: розв’язати методом Крамера систему рівнянь
![]()
Маємо:
![]() ,
,
![]()
![]()
Отже,
![]()
![]()
Відповідь:
![]()
Визначники третього порядку
Визначником (детермінантом) третього порядку називається вираз
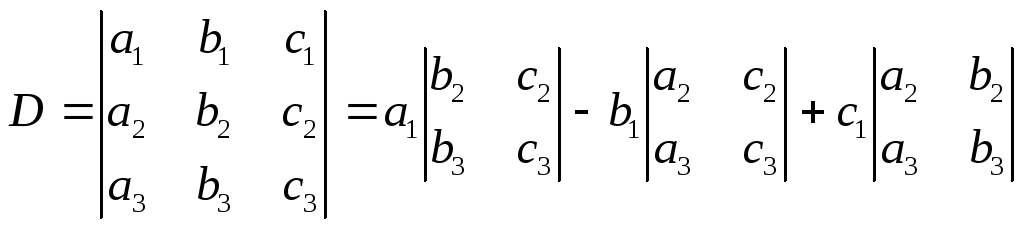 .
(12)
.
(12)
Числа
![]() називаються елементами визначника
(12). Якщо розкрити у формулі (12) всі
визначники другого порядку, одержимо:
називаються елементами визначника
(12). Якщо розкрити у формулі (12) всі
визначники другого порядку, одержимо:
![]() (13)
(13)
Наприклад:
обчислимо визначник
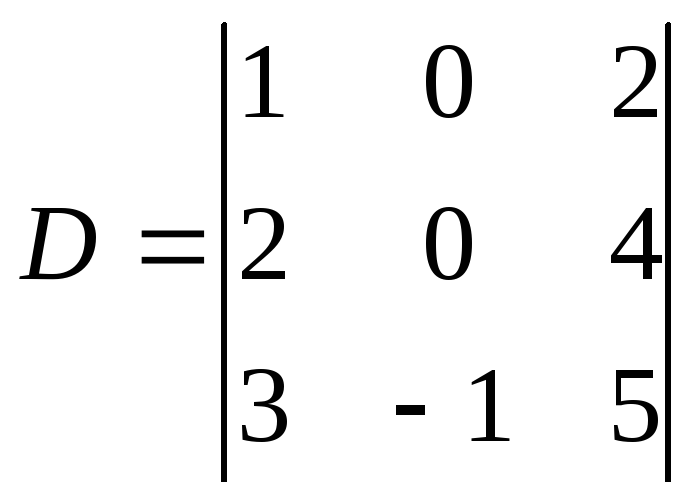 .
Користуючись означенням, маємо:
.
Користуючись означенням, маємо:![]() .
.
Зауважимо, що формулу (13) легко запам’ятати за допомогою так званого правила трикутника.
Так, у
наведеному прикладі із знаком “плюс”
беруть такі добутки:
![]()
![]()
![]() а із знаком “мінус” –
а із знаком “мінус” –![]()
![]() .
Отже,
.
Отже,![]() .
(звичайно, результат обчислення не
залежить від того, яким способом ми
обчислювали визначник – за означенням
чи за правилом трикутника, яке випливає
з означення).
.
(звичайно, результат обчислення не
залежить від того, яким способом ми
обчислювали визначник – за означенням
чи за правилом трикутника, яке випливає
з означення).
Наведемо декілька важливих означень.
Мінором елемента визначника третього порядку називається визначник другого порядку, який одержується з даного визначника у результаті викреслювання строчки і стовпчика, на перетині яких стоїть даний елемент.
Наприклад,
мінор елемента 5 визначника
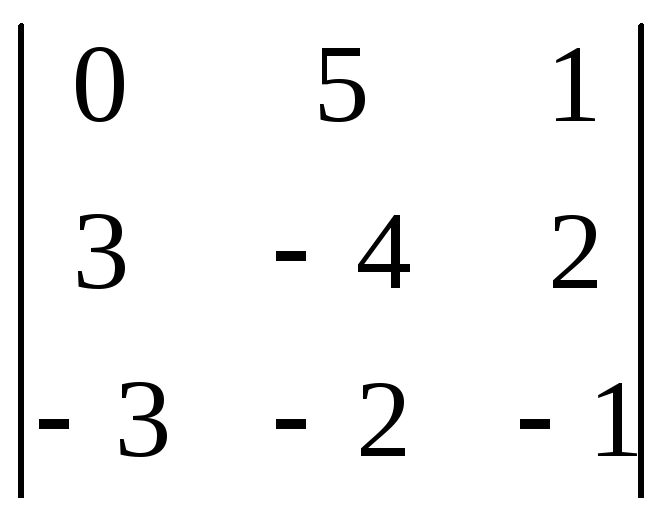 – це визначник
– це визначник![]() .
.
Говорять, що елемент займає парне місце, якщо сума номерів його строчки і стовпчика – число парне, і непарне місце, якщо сума номерів його сторчки і стовпчика – число непарне.
Наприклад, елемент 5 у попередньому прикладі займає непарне місце, бо знаходиться у 1-ій строчці і у 2-му стовпчику, а 1+2=3 – число непарне.
Алгебраїчним доповненням (мінором із знаком) елемента визначника третього порядку називається мінор цього елемента, взятий із знаком “плюс”, якщо елемент займає парне місце, і із знаком “мінус”, якщо непарне місце.
Наприклад,
для визначника вигляду
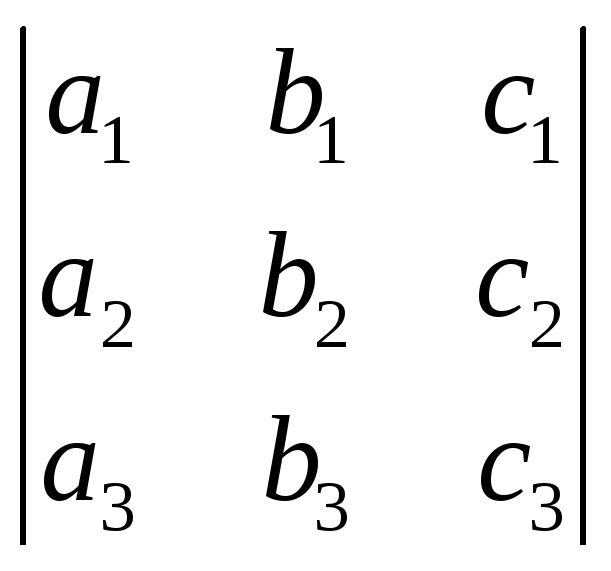 алгебраїчне доповнення елемента
алгебраїчне доповнення елемента![]() – це число
– це число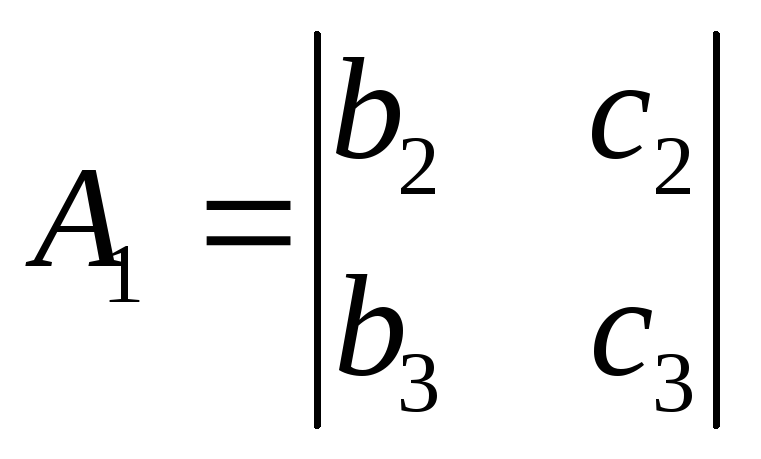 ,
алгебраїчне доповнення елемента
,
алгебраїчне доповнення елемента![]() – це число
– це число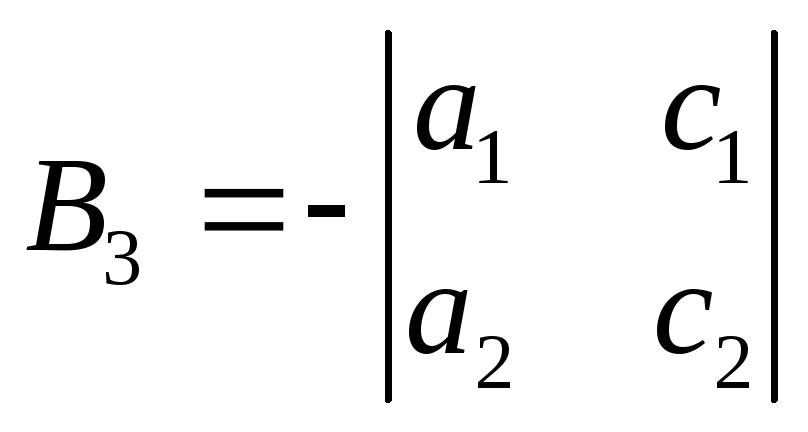 (алгебраїчне доповнення елементів
позначаються відповідними великими
буквами з тими ж самими індексами, які
є у елемента).
(алгебраїчне доповнення елементів
позначаються відповідними великими
буквами з тими ж самими індексами, які
є у елемента).
Якщо
елементи визначника представлені як
![]() (
(![]() – номер строчки,
– номер строчки,![]() – номер стовпчика), тобто якщо
– номер стовпчика), тобто якщо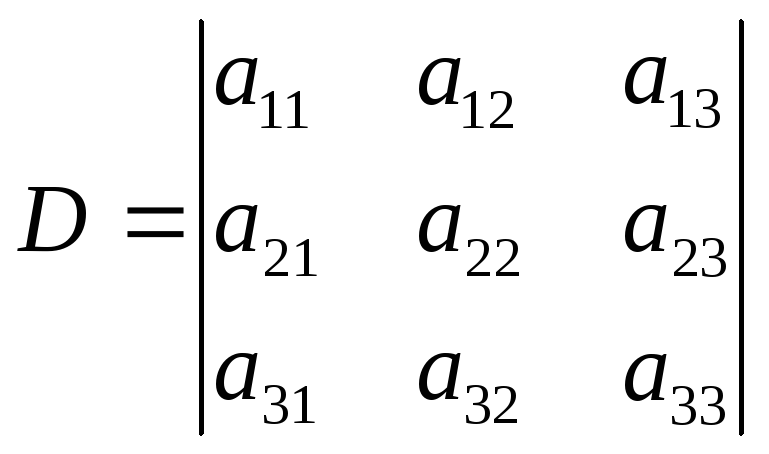 ,
то, позначивши через
,
то, позначивши через![]() мінор елемента
мінор елемента![]() ,
через
,
через![]() – алгебраїчне доповнення елемента
– алгебраїчне доповнення елемента![]() ,
маємо:
,
маємо:
![]() .
.
(Тут
![]() забезпечує зміну знаків: якщо
забезпечує зміну знаків: якщо![]() – число парне, то
– число парне, то![]() ,
а якщо
,
а якщо![]() – число непарне, то
– число непарне, то![]() ).
).
Строчки і стовпчики визначника називають його рядами.
Має місце така теорема про обчислення визначника третього порядку.
Теорема. Визначник третього порядку дорівнює сумі добутків елементів будь-якого ряду визначника на їх алгебраїчні доповнення.
Так,
визначник (12), згідно з означенням, можна
представити так:
![]() .
Безпосередньою перевіркою встановлюємо,
що цей визначник можна обчислювати ще
й за такими формулами (що, власне, і
доводить теорему):
.
Безпосередньою перевіркою встановлюємо,
що цей визначник можна обчислювати ще
й за такими формулами (що, власне, і
доводить теорему):
![]()
![]()
![]()
![]()
![]() .
.
