- •Методичні рекомендації
- •1. Опис навчальної дисципліни
- •2. Структура навчальної дисципліни
- •3. Зміст семінарських занять
- •1. Вектори (основні поняття)
- •2. Лінійні операції з векторами
- •Із означення випливає, що (комутативність).
- •3. Лінійна залежність векторів
- •4. Скалярний добуток векторів
- •Визначники другого порядку
- •Визначники третього порядку
- •Основні властивості визначників
- •Матриці та дії з ними
- •Семінарське заняття 2
- •2. Метод Гаусса
- •3. Розв’язування систем матричним методом
- •4. Ранг матриці та способи його обчислення
- •5. Теорема Кронекера-Капеллі
- •Семінарське заняття 3
- •Тема 3. Пряма, площина. Тема 4. Криві та поверхні другого порядку
- •Виконання студентами тестових завдань з питань теми заняття. Методичні вказівки
- •Пряма, площина
- •1. Різні види рівнянь прямої лінії
- •2. Нормальне рівняння площини
- •3. Загальне рівняння площини
- •4. Рівняння площини у відрізках на осях
- •5. Рівняння площини, яка проходить через дану точку; через дані три точки.
- •6. Кут між двома площинами
- •7. Віддаль від точки до площини
- •8. Пряма лінія у просторі (векторне рівняння; параметричні та канонічні рівняння; пряма як лінія перетину площин)
- •9. Кут між прямими
- •10. Кут між прямою і площиною
- •11. Перетин прямої з площиною
- •Лінії другого порядку
- •Поняття про полярну систему координат
- •Поверхні та їх класифікація
- •2. Поверхні обертання
- •3. Поверхні другого порядку
- •Семінарське заняття 4
- •2. Функція двох змінних
- •3. Нескінченно малі та нескінченно великі величини
- •4. Границя послідовності
- •5. Границя функції
- •Семінарське заняття 5
- •Тема 6. Неперервність функції. Точки розриву
- •Виконання студентами тестових завдань з питань теми заняття. Методичні вказівки
- •Семінарське заняття 6
- •Тема 7. Похідна. Диференціал
- •Виконання студентами тестових завдань з питань теми заняття. Методичні вказівки
- •Похідна, її фізичний, геометричний та економічний зміст
- •2. Диференційовність та неперервність функцій
- •6. Диференціал та його геометричне значення
- •7. Похідні та диференціали вищих порядків
- •8. Формула Тейлора
- •9. Частинні похідні та диференціали функції двох змінних
- •10. Похідна по напряму. Градієнт функції
- •Похідною функції в напрямку (де – точка, що лежить на промені ) називається , деі– значення функції в точкахі. Якщо функція– диференційовна, то має місце формула:
- •Наприклад. Знайти похідну функції в точців напрямку, що утворює з віссюкут в. Розв’язок. Визначимо частинні похідні іта обчислимо їх значення в точці:. Враховуючи, що,
- •11. Диференціювання складних функцій
- •12. Геометричні застосування диференціального числення функції двох змінних
- •13. Похідні і диференціали вищих порядків
- •Семінарське заняття 7
- •2. Правило Лопіталя
- •3. Монотонність функції
- •4.Дослідження на екстремум
- •5. Вигнуті та увігнуті криві
- •6. Вертикальні та похилі асимптоти
- •7. Застосування похідної в економіці
- •Семінарське заняття 8
- •Умовний екстремум
- •3. Метод найменших квадратів
- •Таблиця 1
Семінарське заняття 4
Тема 5. Функціональна залежність. Границя функції і послідовності
Питання для усного опитування та дискусії
5.1. Функція однієї та багатьох змінних.
5.2. Послідовність, її границя.
5.3. Границя функції однієї і багатьох змінних.
5.4. Основні теореми про границі.
5.5. Приклади відшукання границь.
Аудиторна письмова робота
Виконання студентами тестових завдань з питань теми заняття.
Методичні вказівки
Ключовими термінами, на розумінні яких базується засвоєння навчального матеріалу теми, є : функція однієї змінної, функція багатьох змінних, послідовність, границя послідовності, границя функції однієї змінної, границя функції багатьох змінних, перша «чудова» границя, друга «чудова» границя, теореми про границі.
З метою глибокого засвоєння навчального матеріалу при самостійному вивченні теми студенту варто особливу увагу зосередити на таких аспектах.
1. Функція однієї змінної
Якщо
кожному значенню змінної
![]() ,
що належить деякій області, відповідає
одне певне значення другої змінної
,
що належить деякій області, відповідає
одне певне значення другої змінної
![]() ,
то
,
то
![]() єфункція
від
єфункція
від
![]() :
:
![]() .
.
Сукупність
значень
![]() ,
для яких визначаються значення функції
,
для яких визначаються значення функції
![]() в силу правила
в силу правила
![]() ,
називаєтьсяобласть
визначення функції.
,
називаєтьсяобласть
визначення функції.
До основних елементарних функцій відносяться:
1) степенева
функція
![]() (
(![]() - дійсне число);
- дійсне число);
2) показникова
функція
![]() (
(![]() );
);
3) логарифмічна
функція
![]() (
(![]() );
);
тригонометричні функції
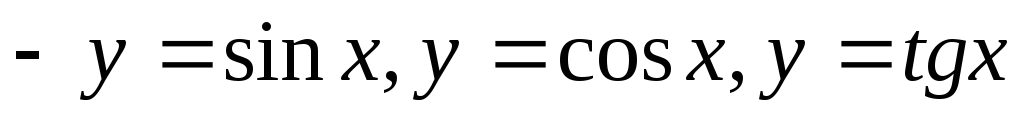 ;
;обернені тригонометричні функції
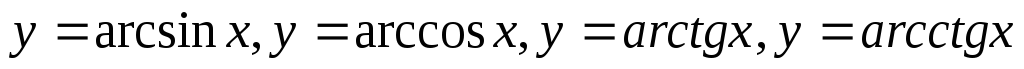 .
Нагадаємо
їх графіки (рис. 1– 5)
.
Нагадаємо
їх графіки (рис. 1– 5)
|
|
|
0
|
а)
![]() –
ціле додатне число
–
ціле додатне число
|
|
y
|
x |
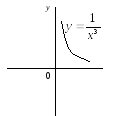
б)
![]() – ціле від'ємне число
– ціле від'ємне число
|
|
|
|
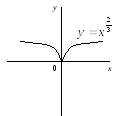
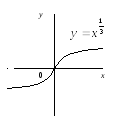
в)
![]() – дробово-раціональне число
– дробово-раціональне число
Рис.1.
Степенева функція
![]()
|
Рис.2.
Показникова функція
|
Рис.3.
Логарифмічна функція
|
|
а)
|
б)
|
Рис.4. Тригонометричні функції
|
а)
|
б)
|
в)
|
г)
|
Рис.5. Обернені тригонометричні функції
Елементарною
функцією
називається функція, яка може бути
заданою однією формулою виду
![]() ,
де вираз справа складений із основних
елементарних функцій і сталих за
допомогою скінченого числа операцій
додавання, віднімання, множення, ділення
і взяття функції від функції.
,
де вираз справа складений із основних
елементарних функцій і сталих за
допомогою скінченого числа операцій
додавання, віднімання, множення, ділення
і взяття функції від функції.
Алгебраїчною
функцією
називається будь-яка функція
![]() ,
яка задовольняє рівняння виду
,
яка задовольняє рівняння виду
![]() ,
,
де
![]() – многочлени від
– многочлени від![]() .
.
До алгебраїчних функцій належать такі елементарні функції:
а) Ціла раціональна функція (многочлен)
![]()
(тут
![]() – коефіцієнти,
– коефіцієнти,![]() – ціле ціле невід’ємне число – степінь
многочлена);
– ціле ціле невід’ємне число – степінь
многочлена);
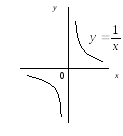
б) Дробово-раціональна функція
![]()
(тут
![]() – коефіцієнти,
– коефіцієнти,![]() ,
,![]() ,
,![]() та
та![]() – цілі невід’ємні числа – степені
многочленів в чисельнику і знаменнику);
– цілі невід’ємні числа – степені
многочленів в чисельнику і знаменнику);
в)
Ірраціональна
функція:
якщо в формулі
![]() в правій частинні виконуються операції
додавання, віднімання, множення, ділення
і піднесення до степеня з раціональними
нецілими показниками, то функція
в правій частинні виконуються операції
додавання, віднімання, множення, ділення
і піднесення до степеня з раціональними
нецілими показниками, то функція![]() називається ірраціональною (наприклад,
називається ірраціональною (наприклад,![]() ).
).
Функція,
яка не є алгебраїчно, називається
трансцендентною
(наприклад,
![]() ).
).









 0
0







 0
0


 0
0














 0
0



 -1
0
-1
0



 -1
0
-1
0


 0
0