Поняття про полярну систему координат

Крім прямокутної декартової системи координат на площині, досить часто користуються полярною системою координат (рис.4).

0

Рис.4. Полярна система координат

Задають полярну вісь , одиницю масштабу і додатний напрям відліку полярного кута(проти руху годинникової стрілки). Положення будь-якої точкина площині визначаєтьсяполярним радіусом точки (її відстанню від полюса) таполярним кутом (між полярною віссю ). Якщо, наприклад, вважати, щота, то будь-якій точціплощини відповідатиме єдина пара чисел– полярні координати цієї точки. І навпаки: знаючи полярні координати точки, її можна однозначно побудувати.

Наведемо графік функції (трьохпелюсткової троянди) в полярній системі координат (рис.5).

0 1

Рис.5. Графік лінії в полярній системі координат

Зауважимо, що, початок декартової системи координат з початкомполярної системи координат, а вісь– з полярною віссю, можна встановити формули зв’язку між декартовими і полярними координатами однієї і тієї ж точ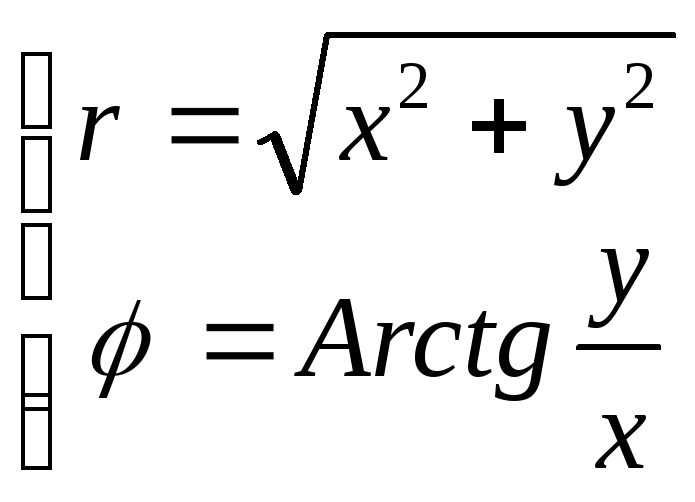ки:;; (знакитаспівпадають).

Студентам рекомендується перевірити ці формули самостійно.

Поверхні та їх класифікація

1. Порядок алгебраїчної поверхні. Циліндр. Конус

Загальне рівняння алгебраїчної поверхні має вигляд , де зліва у рівнянні стоїть цілий многочлен відносно. Степіньцього многочлена визначає порядок алгебраїчної поверхні. Так, наприклад, площина – це поверхня першого порядку. Ми розглянемо поверхні 1-го і 2-го порядку.

а) Циліндричною поверхнею називається поверхня, яка описується прямою, що рухається вздовж даної лінії _L і залишається паралельною деякій даній прямій. При цьому лінія _L називається направляючою, а пряма, що рухається, називається твірною.

Нехай направляюча _L циліндричної поверхні визначається рівняннями:

_.

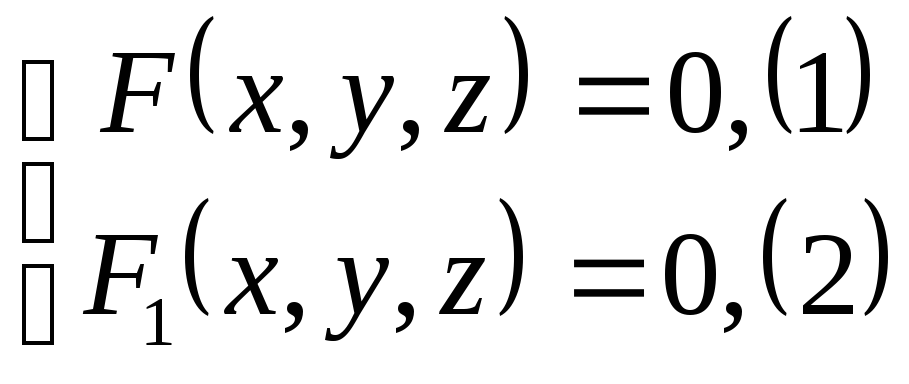Нехай – направляючі коефіцієнти твірних циліндричної поверхні.Канонічні рівняння твірних:

(3)

(4)

Тут – координати точки направляючої, а– змінні координати точки твірної.

Щоб одержати рівняння циліндричної поверхні, слід виключити з рівнянь (1) – (4).

Розглянемо такий приклад. Скласти рівняння циліндричної поверхні, твірні якої паралельні прямій

,

а направляючою є пряма

Розв'язування. Канонічні рівняння твірної мають вигляд

.

Виключаємо з останніх чотирьох рівнянь. Для цього позначимо

.

і виразимо звідси через і:

.

Підставимо ці вирази у рівняння направляючої:

або

Виключимо з останньої системи , одержимо:

.

Це – рівняння площини, яка і є шуканою циліндричною поверхнею.

б) Конічною поверхнею називається поверхня, яка описується прямою, що проходить через дану точку – вершину конуса – і перетинає дану лінію – направляючу конуса. ця пряма в будь-якому її положенні називається твірною конуса.

Нехай направляюча конуса описується рівняннями (1) і (2), а вершина конуса знаходиться в точці (). Твірна конуса – це пряма, яка проходить через дві точки – () та. Ці рівняння такі:

Виключаючи із згаданих чотирьох рівнянь, одержимо рівняння канонічної поверхні.

Наприклад. Скласти рівняння конуса з вершиною в початку координат і направляючою

.

Розв'язування. Рівняння твірної конуса

, або

Оскільки , маємо:

.

Підставивши ці вирази у рівняння , одержимо:

або . Це – рівняння кругового конуса.